ДВП л.р.5 Формула повної ймов і Бейєса (2). Лабораторна робота 4 формула повної ймовірності. Формула бейєса теорема. Ймовірність події, яка може
 Скачать 40.57 Kb. Скачать 40.57 Kb.
|
|
ЛАБОРАТОРНА РОБОТА 4 ФОРМУЛА ПОВНОЇ ЙМОВІРНОСТІ. ФОРМУЛА БЕЙЄСА Теорема. Ймовірність події 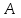 , яка може відбутися лише при умові появи однієї з несумісних подій , яка може відбутися лише при умові появи однієї з несумісних подій 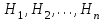 , що утворюють повну групу подій, рівна сумі добутків ймовірностей , що утворюють повну групу подій, рівна сумі добутків ймовірностей 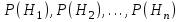 на умовні ймовірності на умовні ймовірності 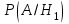 , , 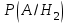 ,..., ,...,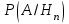 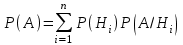 . .Цю формулу називають формулою повної ймовірності. Події 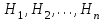 називають гіпотезами. називають гіпотезами.Якщо подія 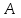 відбулася, то ймовірності гіпотез обчислюють за формулою Бейєса відбулася, то ймовірності гіпотез обчислюють за формулою Бейєса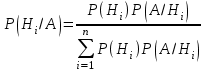 . .Приклад. З 18 стрільців 5 влучають в мішень з ймовірністю 0,8; 7 – з ймовірністю 0,6 і 6 – з ймовірністю 0,5. а) Яка ймовірність того, що навмання обраний стрілець у мішень не влучив. б) Навмання обраний стрілець зробив постріл, але в мішень не влучив. До якої з груп найімовірніше належить цей стрілець? Розв’язання. Нехай подія А – стрілець в мішень не влучив. Гіпотези: 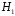 – стріляв стрілець 1-ї групи; – стріляв стрілець 1-ї групи; 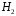 – стріляв стрілець 2-ї групи; – стріляв стрілець 2-ї групи; 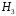 – стріляв стрілець 3-ї групи. – стріляв стрілець 3-ї групи.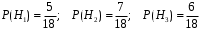 . .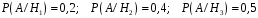 . .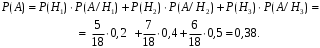 б) 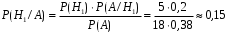 . .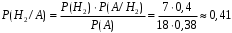 . .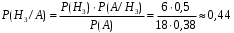 . .Стрілець найімовірніше належав до третьої групи. |
