Лабораторная работа №1 численные методы 2 курс. Лаборторна Робота №1 виправлена. Лабораторна робота теорія похибок

• Название: Лабораторна робота теорія похибок
• Анкор: Лабораторная работа №1 численные методы 2 курс
• Дата: 25.10.2022
• Размер: 6.35 Mb.
• Имя файла: Лаборторна Робота №1 виправлена .docx
• Тип: Лабораторна робота; #754509

ЛАБОРАТОРНА РОБОТА 1.

ТЕОРІЯ ПОХИБОК

Виконав: Мінаєв Олексій

Варіант №12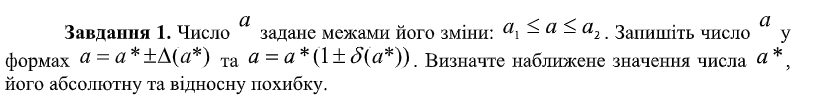





Розв’язання

1. 
   Знаходимо значення а^*: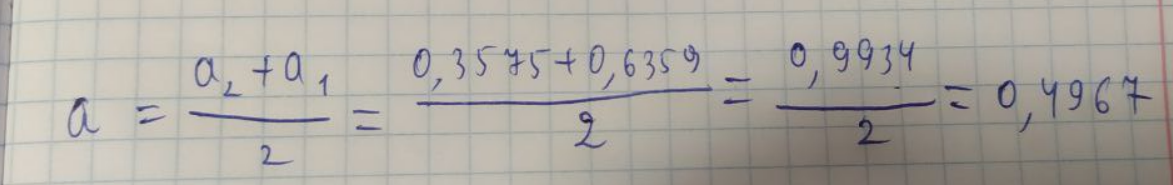
   

2. 
   Знаходимо значення абсолютної похибки: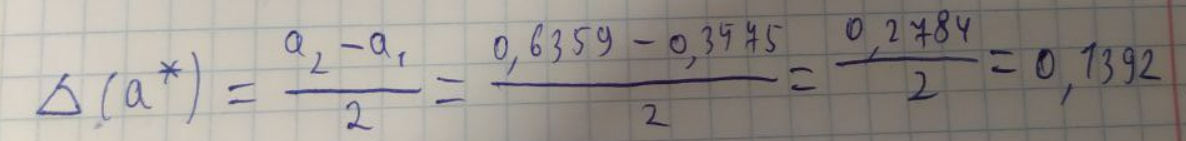
   

3. 
   Заходимо значення відносної похибки: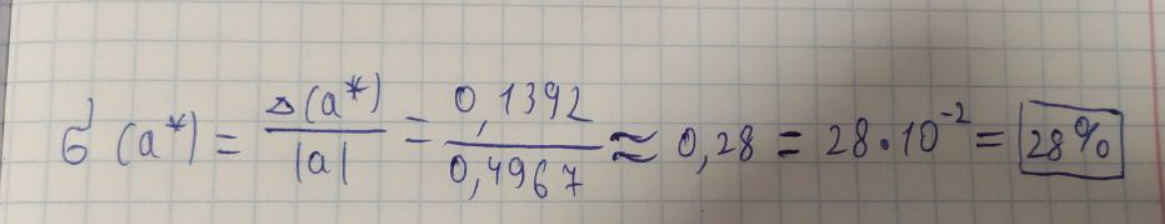
   

4. 
   Записуємо відповідь: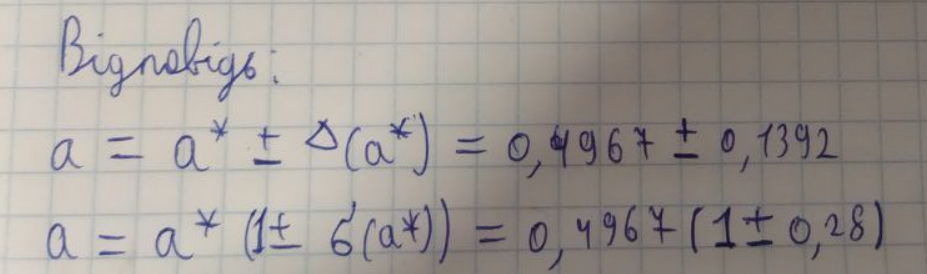
   

Розв’язання

1. 
   Для а:
   

Дано . Значущими цифрами числа є всі цифри, починаючи з першої ненульової зліва, тобто усі цифри цього числа, а саме 45.0501.

Оскільки абсолютна похибка дорівнює 9*10^-4, то останньою вірною буде цифра, що відповідає розряду 10^-3 , тобто цифра «0». Всього значущих цифр буде 4. Остаточно отримаємо запис числа з підкресленими вірними цифрами: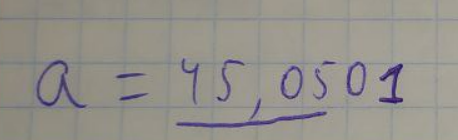

2. 
   Для b:
   

Дано . Значущими цифрами числа є всі цифри, починаючи з першої ненульової зліва, тобто цифри 734 (всього 3 значущі цифри).

Оскільки абсолютна похибка дорівнює 1*10^-5, то останньою вірною буде цифра, що відповідає розряду 10^-4 , тобто цифра «7». Всього значущих цифр буде 1. Остаточно отримаємо запис числа з підкресленими вірними цифрами: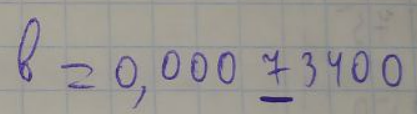







Розв’язання

Оскільки значення змінних написані з усіма вірними цифрами, то: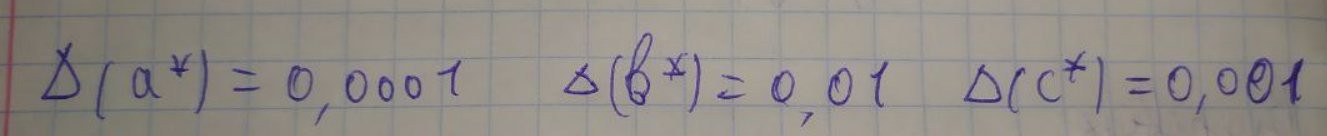



Відносні похибки дорівнюють:

1. 
   Оцінимо похибку, використовуючи формулу для оцінки похибки арифметичних операцій.
   

Спочатку обчислимо величину ab та оцінимо похибку. Маємо: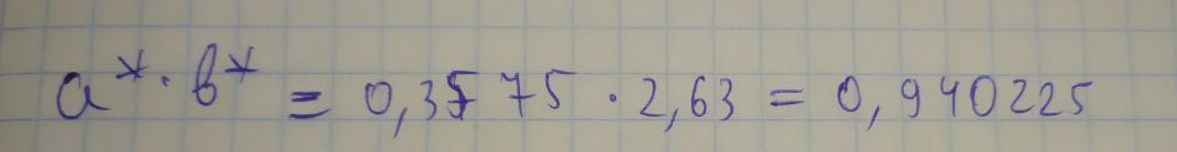



Відносна похибка добутку не перевищує суми відносних похибок множників, тобто: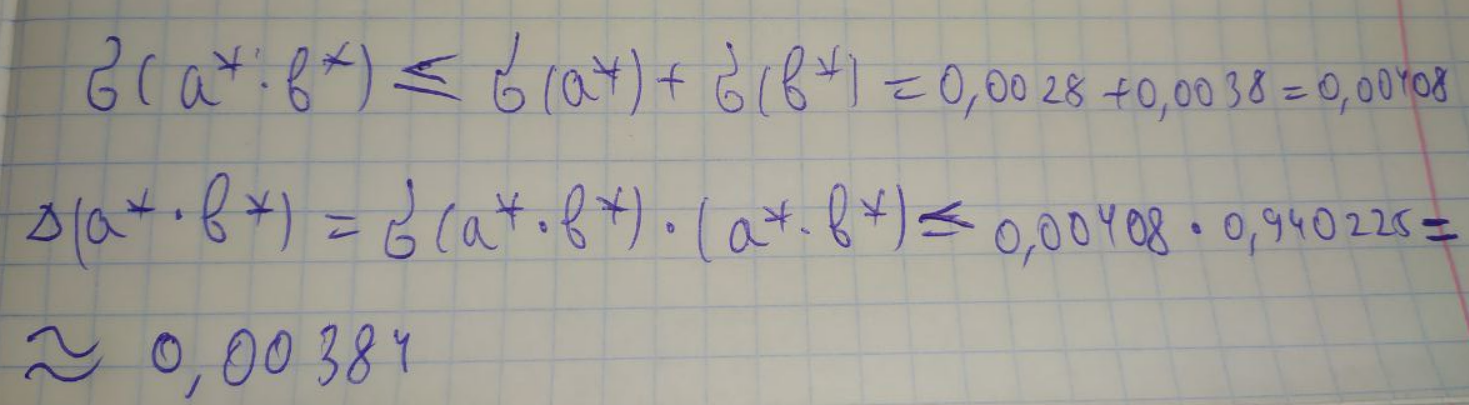



Далі обчислимо величину c² та оцінимо похибку. Маємо: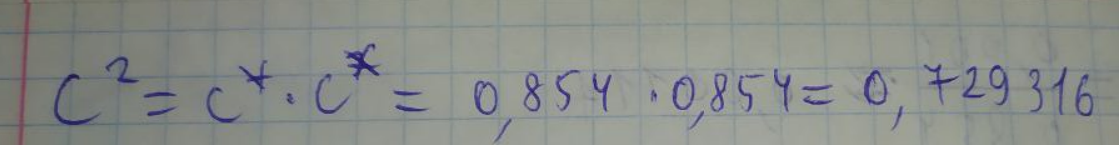



Відносна похибка добутку не перевищує суми відносних похибок множників, тобто: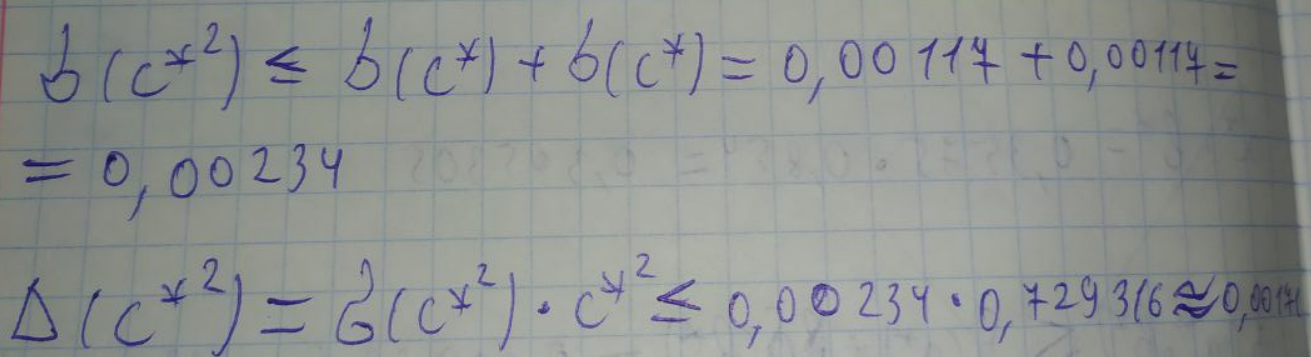



Заключна операція – операція ділення. Маємо: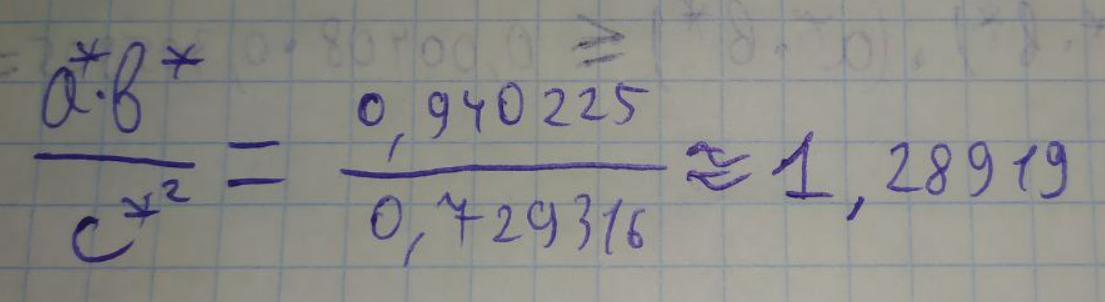



Як і для множення, відносна похибка результату не перевищує суми відносних похибок чисельника та знаменника, тобто: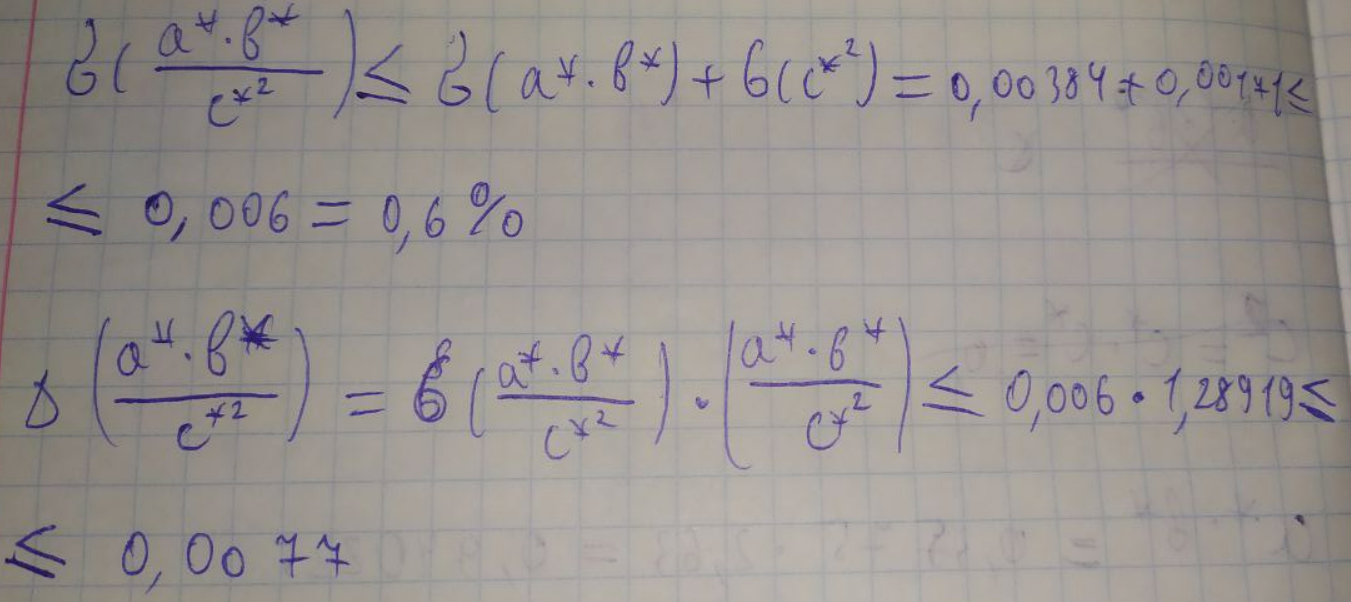



Таким чином:



Вірними є тільки цифри перед десятковою комою, тобто, з урахуванням вірних цифр: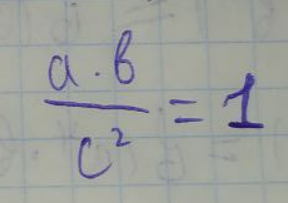

2. 
   Оцінимо похибку, використовуючи формулу для оцінки похибки обчислення функції. Знайдемо частинні похідні функції: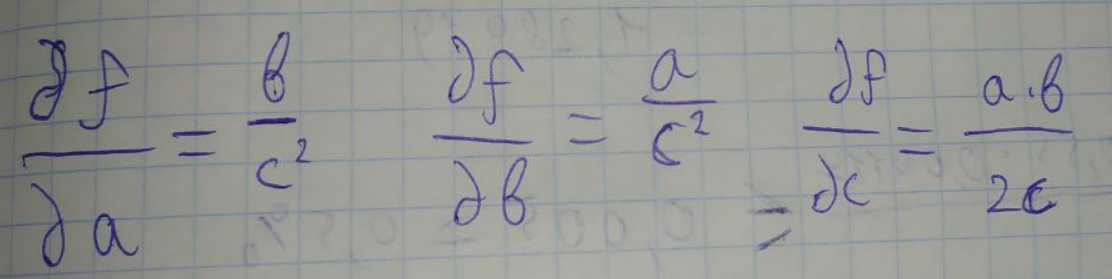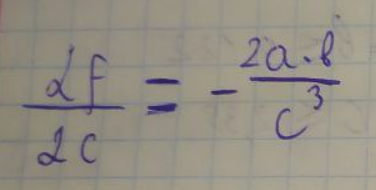
   

\

Виділимо межі зміни аргументів для визначення максимуму похідних: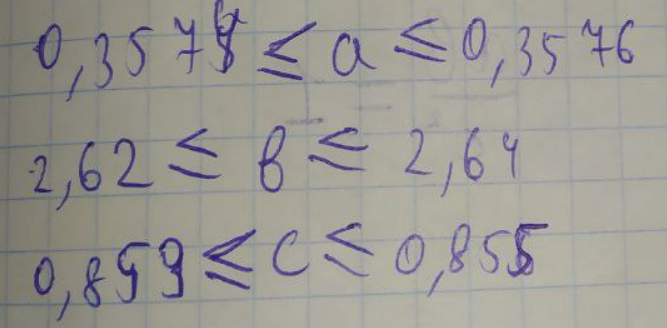



Обчислюємо максимальні значення похідних на вказаних проміжках: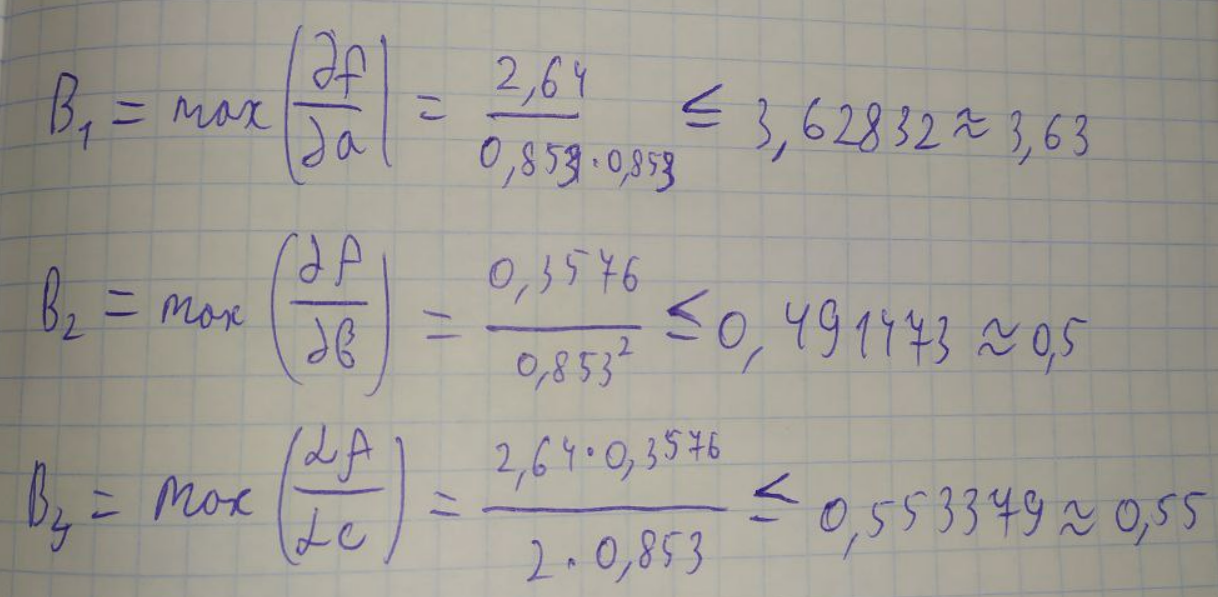





Підставляємо отримані значення і дані абсолютні похибки у формулу (1) для абсолютної похибки обчислення функції:



Відносну похибку обчислення значення функції отримаємо за формулою (2)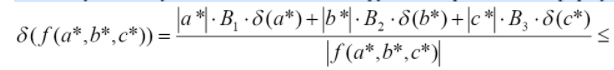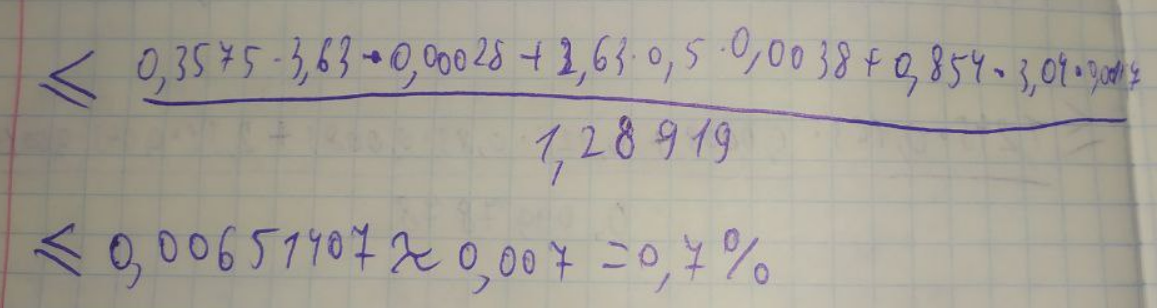



Таким чином, оцінюючи похибку другим способом, отримаємо: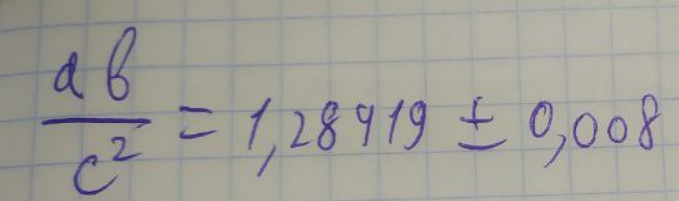



Вірними є тільки цифри перед десятковою комою, тобто, з урахуванням вірних цифр: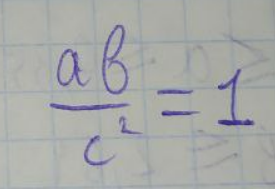