геофизика. отчет к лабе 1 геофизика. Лабораторная работ 1

• Название: Лабораторная работ 1
• Анкор: геофизика
• Дата: 15.10.2020
• Размер: 38.37 Kb.
• Имя файла: отчет к лабе 1 геофизика.docx
• Тип: Задача; #143155

Лабораторная работ № 1

Гравитационное моделирование простых геометрических тел.

Задача работы:

– выполнить расчёты гравитационного поля точечной массы, горизонтального цилиндра, материальной полосы небольшой и средней ширины, а также вертикального цилиндра;

– определить соотношение характерных точек аномалий с параметрами залегания аномальных тел;

– отразить результаты в отчёте по лабораторной работе.

Методика выполнения

Работа выполняется в доступной электронной среде, позволяющей проводить вычисления по аналитическим формулам (MS Excel, LibreOffice Calc, Grapher, etc.). В качестве исходных данных используются таблица вариантов (таблица 1). В соответствии с нижеприведёнными формулами и вариантом студента рассчитываются гравитационные аномалии 5 видов аномальных тел. Для каждого графика определяется ширина аномалии (W₁) на половине высоты, а также ширина отрезка, формируемого касательными на оси абсцисс (W₂). Вычисляется отношение W₁ / h и W_ / h.

Опорная информация

Гравитационное поле большинства простых геометрических тел описывается несложными аналитическими выражениями.

1. 
   Материальная точка
   

Δg = γΔMh/(x² + h²)^3/2

2. 
   Горизонтальный стержень (бесконечный по оси у)
   

Δg = 2γΔλh/(x² + h²)

3. 
   Вертикальный материальный стержень
   

Δg = 2γΔλ/(x² + h²)^1/2

4. 
   Материальная полоса
   

Δg = 2arctg((l – x) / h) + arctg((l + x) / h)

Здесь Δg – расчётное гравитационное поле м/с², – гравитационная постоянная (6.674·10⁻¹¹ м³·с ⁻²·кг ⁻¹), M – избыточная масса, кг, х – расстояние от точки наблюдения до центра аномального объекта, h – его глубина, избыточная погонная плотность, кг/м, – избыточная поверхностная плотность кг/м², l – ширина материальной полосы.

Таблица 1

Вариант	1		2			3			4				5
	h	M		h			h			h	l			h	l	
2	155	190		200	173		132	167		177	1	166		110	70	120

Совмещенные графики: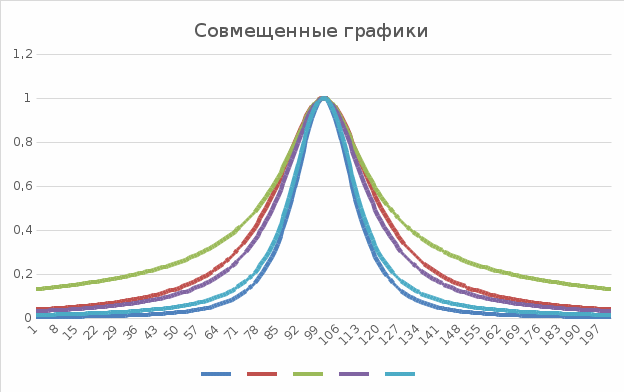


Рисунок 1. График Аномалий

Ряд 1 – точка

Ряд 2 – горизонтальный стержень

Ряд 3 – вертикальный стержень

Ряд 4 – узкая полоса

Ряд 5 – широкая полоса
Таблица соотношений:

	h	w1	w2	h/w1	h/w2
Точка	155	240	160	0,645833	0,96875
Горизонтальный стержень	200	400	240	0,5	0,833333
Вертикальный стержень	132	440	180	0,3	0,733333
Узкая полоса	177	300	200	0,59	0,885
Широкая полоса	110	240	180	0,458333	0,611111

Ответы на вопросы:

График материальной точки самый узкий. Это связано с тем, что материальная точка создает гравитационные поля, сумма которых гораздо меньше, чем сумма полей других аномалий. Это можно подтвердить формулой 1, из которой следует, что аномалия обратно пропорциональна удалению точки наблюдения от центра тела. Вся масса и плотность сконцентрированы в одной точке, в результате чего дополнительное воздействие на гравиметр не происходит. Другими словами, у материальной точки нет других точек, которые могли бы оказать воздействие на измерения.

Δg = γΔMh/(x² + h²)^3/2(1)