Импеданс. БФ_12 Импеданс_тканей_организма. Лабораторная работа бф12 исследование частотной зависимости импеданса тканей организма приборы и принадлежности
 Скачать 61.03 Kb. Скачать 61.03 Kb.
|
|
ЛАБОРАТОРНАЯ РАБОТА № БФ-12 ИССЛЕДОВАНИЕ ЧАСТОТНОЙ ЗАВИСИМОСТИ ИМПЕДАНСА ТКАНЕЙ ОРГАНИЗМА Приборы и принадлежности: генератор переменного напряжения, осциллограф, набор сопротивлений и конденсаторов для сборки исследуемых электрических цепей. Ткани организма проводят не только постоянный, но и переменный ток. Опытным путём было доказано, что сила тока, проходящая через биологическую ткань, опережает по фазе приложенное напряжение. Это позволяет сделать вывод о том, что ёмкостное сопротивление тканей больше индуктивного. В предположении, что индуктивным сопротивлением можно пренебречь, по сравнению с ёмкостным, моделирование электрических свойств биологических тканей можно осуществлять, используя резисторы, которые обладают активным сопротивлением, и конденсаторы – носители ёмкостного сопротивления. Такая модель называется эквивалентной электрической схемой тканей организма. Поскольку ёмкостное сопротивления 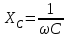 зависит от частоты переменного напряжения зависит от частоты переменного напряжения 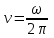 , импеданс (полное сопротивление) тканей также будет зависеть от частоты. График частотной зависимости (дисперсия) импеданса мышечной ткани lgZ=f(υ) представлен на рис.1. Из графика видны две особенности этой зависимости: общее уменьшение импеданса с увеличением частоты, а также наличие трёх областей, где величина импеданса практически не изменяется с ростом частоты. Обычно эти участки называются областями α-, β- и γ- дисперсии импеданса. , импеданс (полное сопротивление) тканей также будет зависеть от частоты. График частотной зависимости (дисперсия) импеданса мышечной ткани lgZ=f(υ) представлен на рис.1. Из графика видны две особенности этой зависимости: общее уменьшение импеданса с увеличением частоты, а также наличие трёх областей, где величина импеданса практически не изменяется с ростом частоты. Обычно эти участки называются областями α-, β- и γ- дисперсии импеданса.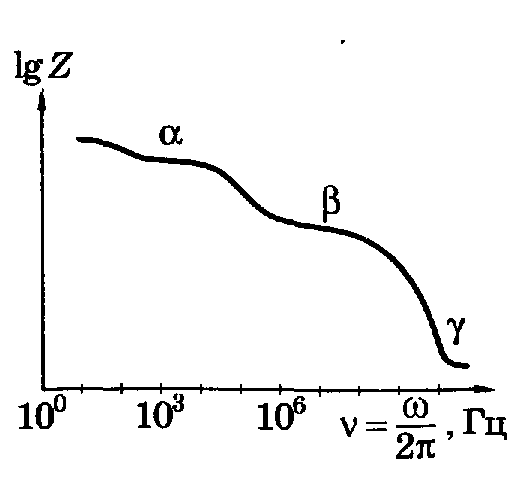 Рис.1. Частотная зависимость импеданса мышечной ткани. Возможные эквивалентные электрические схемы (модели) тканей организма представлены на рис.2 (а, б, в). 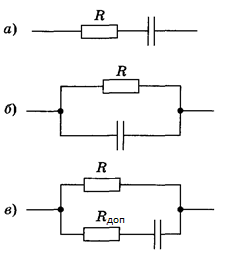 Рис. 2. Эквивалентные электрические схемы тканей организма. Расчётное значение импеданса Z для каждого случая можно получить, используя соответственно формулы (1-3): 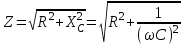 (1), (1),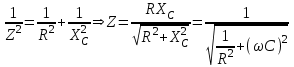 (2), (2),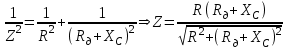 (3). (3).Величину импеданса можно также определить экспериментально. Если к источнику переменного напряжения, в роли которого выступает генератор, последовательно подключить исследуемую схему с сопротивлением Z и известное дополнительное сопротивление 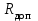 , то, используя закон Ома для участка цепи, можно записать: , то, используя закон Ома для участка цепи, можно записать: 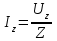 , , 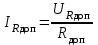 , ,где 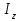 и и 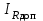 – амплитудные значения силы токов, протекающих через сопротивления Z и Rдоп; Uz и URдоп – падение напряжений на соответствующих сопротивлениях. – амплитудные значения силы токов, протекающих через сопротивления Z и Rдоп; Uz и URдоп – падение напряжений на соответствующих сопротивлениях. Поскольку токи будут одинаковы, получим: 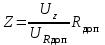 Таким образом, цель работы заключается в проведении теоретического анализа функциональной зависимости Z=f(υ) для рассматриваемых схем на предмет соответствия результатам, полученных опытным путём для реальных тканей (рис.1), а также экспериментальном подтверждении полученных выводов. Выполнение работы Рассчитайте для каждой из трёх схем значение импеданса Z при υ = 1, 2, 5, 10, 30, 40, 50, 100, 500, 1000, 3000, 5000, 10000, 15000 и 20000 Гц. Постройте графики зависимости Z=f(lnυ). Сделайте выводы, какая из схем наиболее точно моделирует импеданс тканей организма. Примечание: значения R, C, Rдоб, необходимые для расчётов, уточнить у преподавателя. Расчёты и построение функциональных зависимостей рекомендуется выполнять с использованием программных автоматизированных комплексов (например, MS Excel, Origin или им подобных). Соберите схему (рис. 2, а), последовательно подключите к ней известное сопротивление 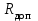 . Запитайте полученную схему от источника переменного напряжения (генератора). При помощи осциллографа для значений частот, аналогичных теоретическому исследованию, определите Uz и URдоп; вычислите Z. Постройте график зависимости Z=f(lnυ) и сравните с полученными теоретическими результатами. Проделайте подобный эксперимент с двумя другими схемами. . Запитайте полученную схему от источника переменного напряжения (генератора). При помощи осциллографа для значений частот, аналогичных теоретическому исследованию, определите Uz и URдоп; вычислите Z. Постройте график зависимости Z=f(lnυ) и сравните с полученными теоретическими результатами. Проделайте подобный эксперимент с двумя другими схемами. Контрольные вопросы Литература Ремизов А.Н., Максина А.Г., Потапенко А.Я. Медицинская и биологическая физика. М.: Дрофа, 2003. – 558 с. (Глава 14). |
