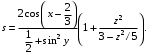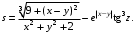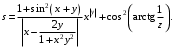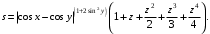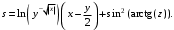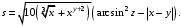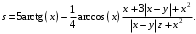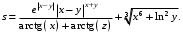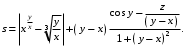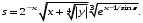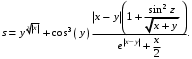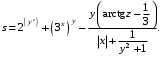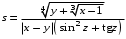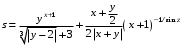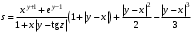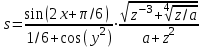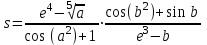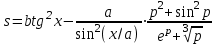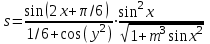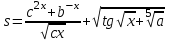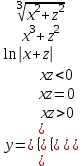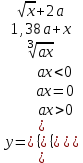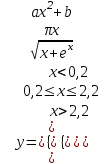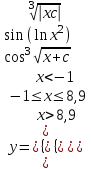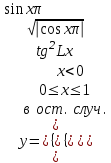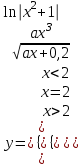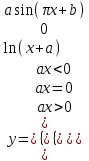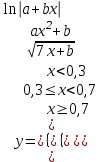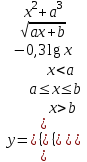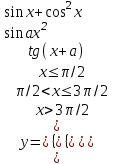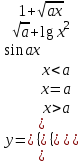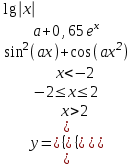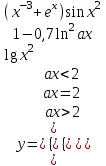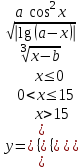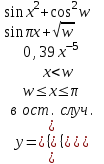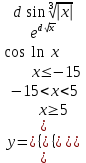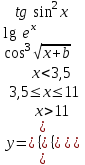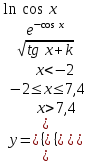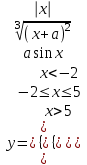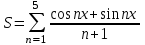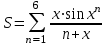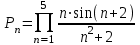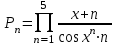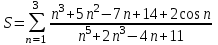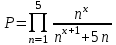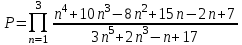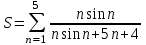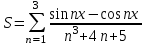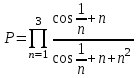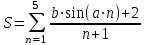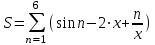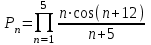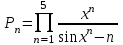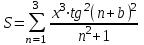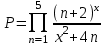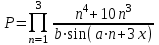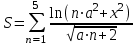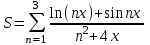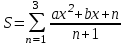Лабораторная работа _Основы программирования на Python_. Лабораторная работА ( ii семестр) Тема Основы программирования на Python 2 Методические указания по выполнению лр
 Скачать 5.35 Mb. Скачать 5.35 Mb.
|
|
ЛАБОРАТОРНАЯ работА (II семестр) Тема 1. Основы программирования на Python1.2 Методические указания по выполнению ЛР Программирование - уникальный предмет, где обучающийся сталкивается с инженерным искусством как таковым. В так называемых инженерных дисциплинах обучение носит по большей части теоретический характер, расчеты просты и до проектирования конструкций, которые будут реально воплощены в "железе", дело никогда не доходит. Другое дело - программирование. В нем каждый имеет возможность проектировать, создавать и пользоваться в реальном виртуальном мире своего компьютера инженерными конструкциями собственного приготовления. Доступность, дешевизна, гибкость, практическая значимость программирования ставят эту дисциплину вне конкуренции как полигон для подготовки инженера или исследователя в любой области техники - ведь принципы инженерного искусства везде одни и те же. В этом смысле рядом с программированием можно поставить разве что электронные конструкторы типа Arduino. Но последние и сложнее, и специфичнее, и дороже. О программе: Самым популярным языком, используемым для программирования, является Python. Python считается интерпретируемым языком. Это означает, что вы можете написать программу или скрипт и выполнить его непосредственно, а не компилировать его в машинный код. Это обеспечивает некоторое удобство программирования и запуска кода для новичков, которые пока не слишком хотят лезть в такие сложности как компилирование, отладка и прочие моменты, так приятные опытным программистам. Помимо быстрого исполнения кода Python обладает другими преимуществами, не свойственными большинству интерпретируемых языков. Например, в Python вам не нужно явно указывать тип переменной (число, строка, список). Интерпретатор определяет типы данных при выполнении скрипта. Интерпретатор Python может работать двумя способами: как интерактивная оболочка для выполнения отдельных команд или в качестве программы с командной строкой для выполнения автономных скриптов. Интегрированная среда разработки (IDE) Python называется IDLE с ней и будем работать. 1.2.1.Установка программы: Для того, чтобы начать работать в Питон, необходимо иметь его интерпретатор на своем компьютере. Скачать дистрибутив совершенно бесплатно можно тут: https://www.python.org/downloads/windows/ Надо скачать версию, не ниже Python 3.7, потому что они создают неудобства при работе с русским алфавитом. IDLE не нравятся русские буквы в тексте программы и вам предлагается явно задать кодировку, например: "# -*- coding: cp1251 -*-". В версиях, не ниже Python 3.7 таких проблем нет. Запуск программы: После установки Python, запускаем оболочку IDLE.  Появляется окно  Что такое IDLE? Это так называемая интегрированная среда разработки (Integrated Development Environment), разработанная создателями Python для облегчения программирования. Это одно из двух основных окон IDLE, с которыми вам предстоит работать. Его называют окном интерпретатора или окном командной строки. У интерпретатора есть замечательное свойство: как только будет введена команда, Python тут же исполнит ее и выведет на экран полученный результат. Фактически перед вами очень мощный и удобный калькулятор! Попросим Python что-нибудь напечатать, например: " АГдс, ГРдс, ГБдс, МПдс". 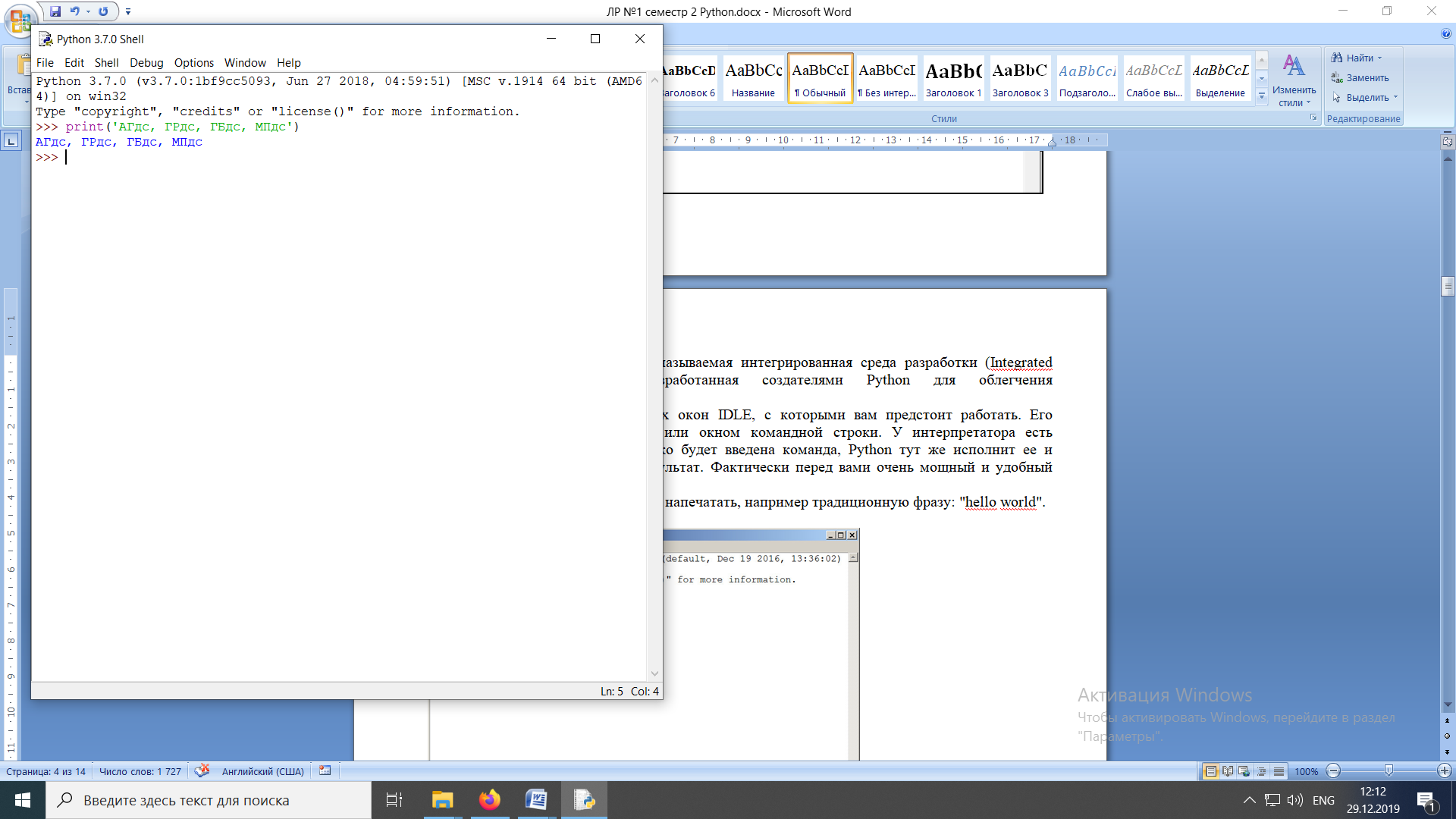 Значки '>>>' играют роль приглашения: Python сигнализирует, что готов считывать новую команду. Также, обратите внимание, после ввода команды Python тут же выводит, что получилось в результате ее выполнения. Попробуем еще несколько команд. 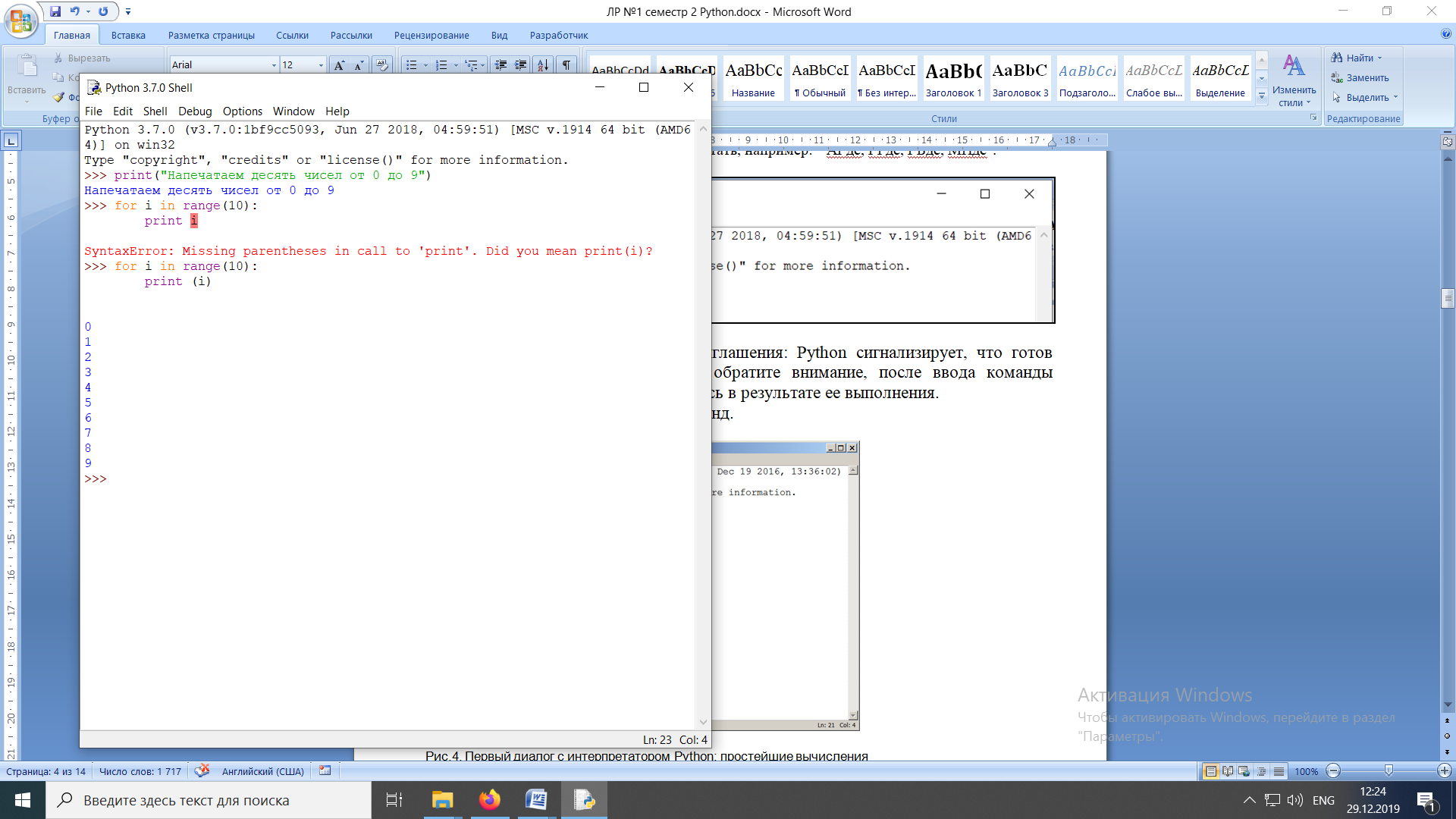 В окне IDLE показан результат запуска новых команд. Не слишком беспокойтесь о том, как правильно программировать: сейчас мы экспериментируем с Python, вводя в него команды. Если что-то не работает, интерпретатор выдает ошибку «SyntaxError: Missing parentheses in call to 'print'. Did you mean print(i)?». В данном случае оператор print i записан ошибочно, исправляем ошибку на print (i) и пробуем снова. Хорошо, теперь зададимся вопросом: если закрыть Python и снова запустить его, как компьютер вспомнит, что мы напечатали? Никак. Нельзя напрямую сохранить содержимое окна интерпретатора, потому что в него входят и сами команды, и ответы системы, например значки '>>>' . Вместо этого мы создадим файл, в котором будут только команды, и сохраним его как документ с расширением *.py. Этот файл всегда можно открыть и запустить в Python, экономя время на повторном наборе всех его команд. Попробуем. Начнем с чистого листа, открыв новое окно. В меню выбираем File -> New File. 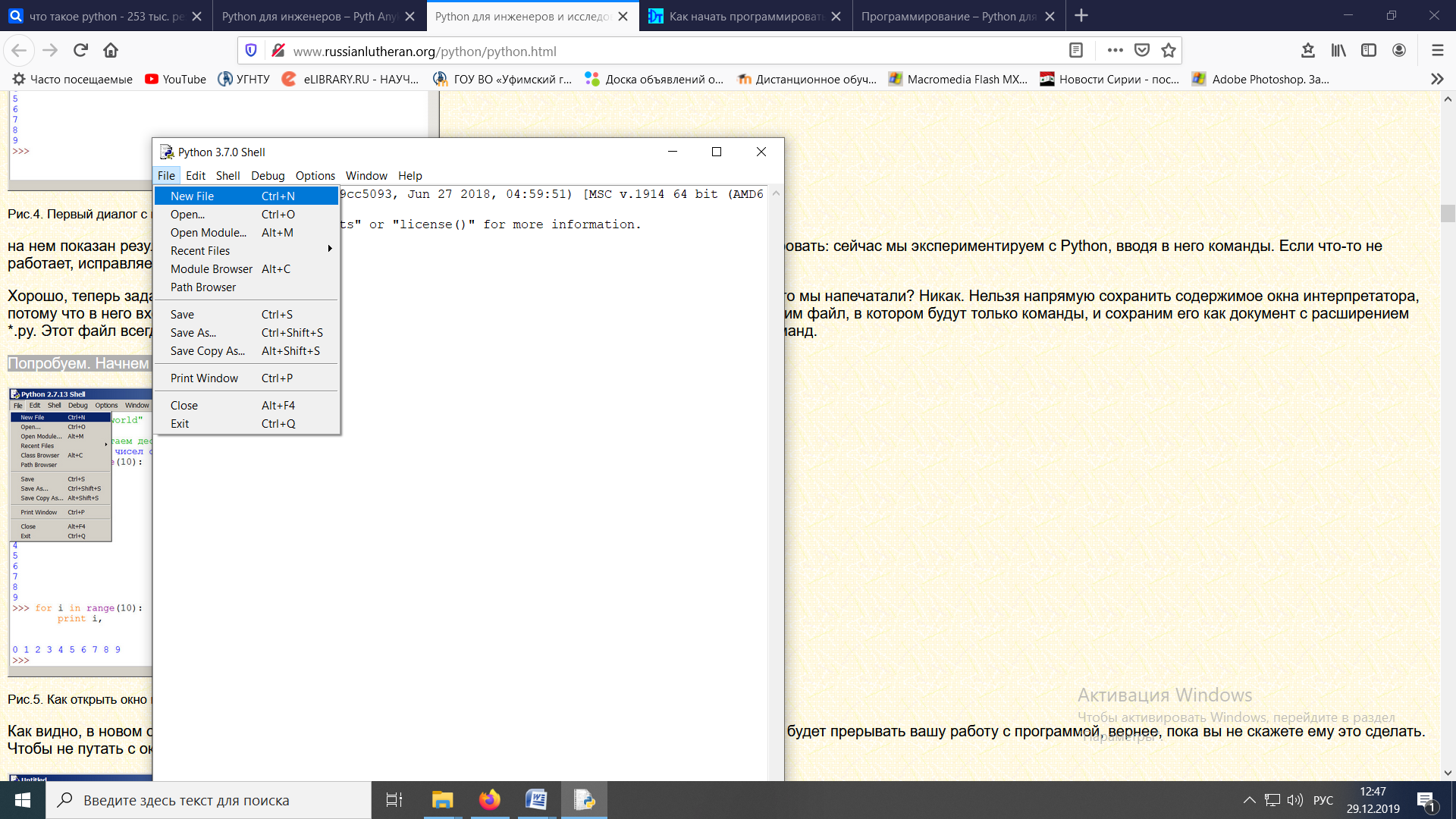 Появляется новое окно.  Как видно, в новом окне ничего нет - оно целиком и полностью отдано под команды. Теперь Python не будет прерывать вашу работу с программой, вернее, пока вы не скажете ему это сделать. Чтобы не путать с окном интерпретатора, назовем его "окном программ". Все, что мы хотели сделать,- это сохранить несколько строк, уже опробованных в окне интерпретатора. Реализуйте этот план, скопировав и вставив эти команды в окно программ. Не забудьте при этом удалить приглашения ">>>", потому что они в программу не входят. Интерпретатор использует их, чтобы напомнить, что вы работаете в интерпретаторе. Но сейчас при редактировании отдельного файла эти артефакты интерпретатора совершенно ни к чему.  Запускаем файл на выполнение: находим в главном меню пункт Run, подпункт Run Module или просто нажимаем быструю клавишу F5. 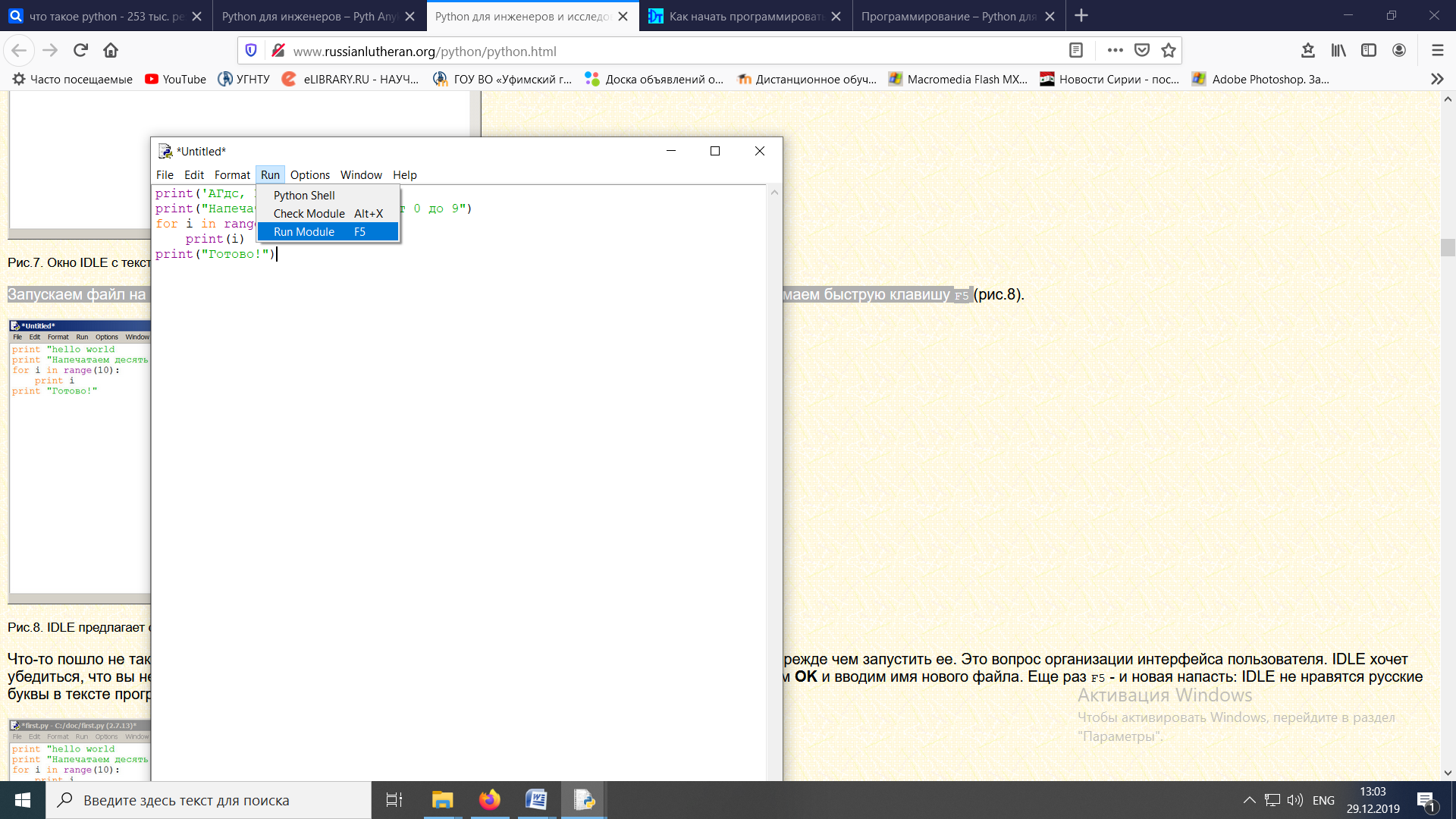 Выйдет сообщение:  IDLE требует сохранять любое окно с программой, прежде чем запустить ее. Это вопрос организации интерфейса пользователя. IDLE хочет убедиться, что вы не забыли сохранить свою работу, перед тем как начнете ее проверять в деле. Что ж, жмем OK и вводим имя нового файла, например Лаб_раб №1_1 (можно указать папку, куда следует сохранить файл) и нажимаем Сохранить. Появляется окно интерпретатора с результатами выполнения программы. Все в порядке.  В заключение убедимся, что созданный файл можно будет загрузить снова. Закрываем все окна IDLE и начинаем с чистого листа. Найдите команду Recent Files (последние файлы) в меню File: появится список, в котором на первом месте - ваша новая программа. Выберите ее, и она появится в окне программ.  Итак, вы овладели начальными навыками работы с Python. Теперь можно применить их в деле. 1.2.2.основные функции и операторы: Модуль math. Тригонометрические функцииЧтобы использовать тригонометрические функции в программе, нужно подключить модуль math import math Пример. Требуется вычислить значение выражения: 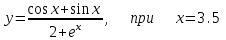 Составим программу: 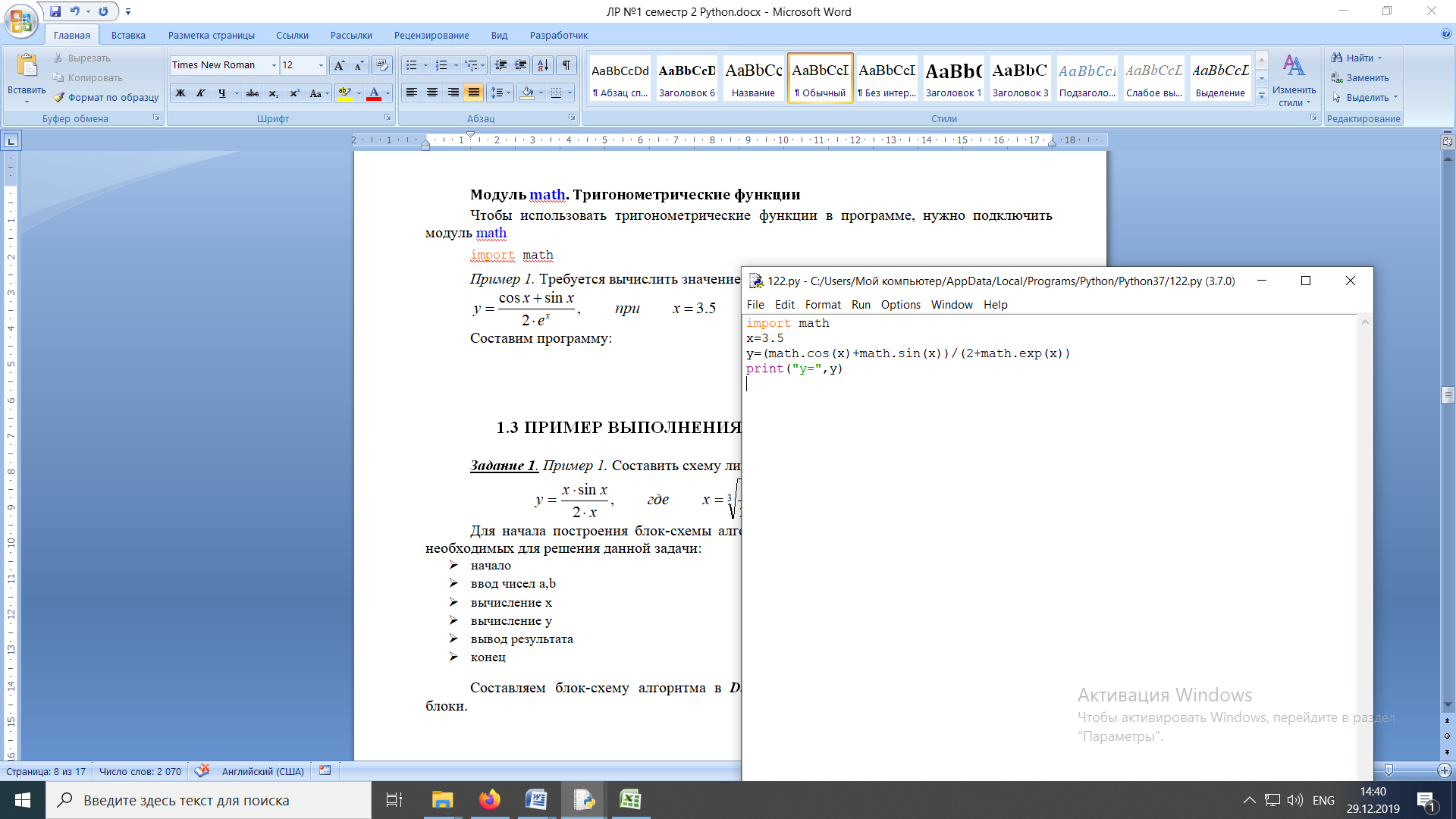 Получим результат  Модуль math – один из важнейших в Python. Этот модуль предоставляет обширный функционал для работы с числами, который приведен в приложении (см. ПРИЛОЖЕНИЕ 1). Условный оператор if. Ход выполнения программы может быть линейным, т.е. таким, когда выражения выполняются, начиная с первого и заканчивая последним, по порядку, не пропуская ни одной строки кода. Но чаще бывает совсем не так. При выполнении программного кода некоторые его участки могут быть пропущены. Поэтому при написании алгоритмов используется еще и ветвление: if a > b: c = a else: c = b Этот кусок кода на Python интуитивно понятен каждому, кто помнит, что if по-английски значит "если", а else - "иначе". Оператор ветвления имеет в данном случае две части, операторы каждой из которых записываются с отступом вправо относительно оператора ветвления. Более общий случай - оператор выбора - можно записать с помощью следующего синтаксиса (пример вычисления знака числа): if a < 0: s = -1 elif a == 0: s = 0 else: s = 1 Стоит заметить, что elif - это сокращенный else if. Без сокращения пришлось бы применять вложенный оператор ветвления: if a < 0: s = -1 else: if a == 0: s = 0 else: s = 1 В условной инструкции может отсутствовать слово else и последующий блок. Такая инструкция называется неполным ветвлением. Например, если дано число x и мы хотим заменить его на абсолютную величину x, то это можно сделать следующим образом: Пример. if x < 0: x = -x print(x) В этом примере переменной x будет присвоено значение -x, но только в том случае, когда x<0. А вот инструкция print(x) будет выполнена всегда, независимо от проверяемого условия. Для выделения блока инструкций, относящихся к инструкции if или else, в языке Python используются отступы. Все инструкции, которые относятся к одному блоку, должны иметь равную величину отступа, то есть одинаковое число пробелов в начале строки. Рекомендуется использовать отступ в 4 пробела и не рекомендуется использовать в качестве отступа символ табуляции. Вложенные условные инструкции Внутри условных инструкций можно использовать любые инструкции языка Python, в том числе и условную инструкцию. Получаем вложенное ветвление – после одной развилки в ходе исполнения программы появляется другая развилка. При этом вложенные блоки имеют больший размер отступа (например, 8 пробелов). Покажем это на примере программы, которая по данным ненулевым числам x и y определяет, в какой из четвертей координатной плоскости находится точка (x,y): Пример. x = int(input()) y = int(input()) if x > 0: if y > 0: # x>0, y>0 print("Первая четверть") else: # x>0, y<0 print("Четвертая четверть") else: if y > 0: # x<0, y>0 print("Вторая четверть") else: # x<0, y<0 print("Третья четверть") В этом примере использовали комментарии - текст, который интерпретатор игнорирует. Комментариями в Питоне является символ # и весь текст после этого символа до конца строки. Операторы сравнения Как правило, в качестве проверяемого условия используется результат вычисления одного из следующих операторов сравнения: < -меньше - условие верно, если первый операнд меньше второго. > - больше - условие верно, если первый операнд больше второго. <= - меньше или равно. >= - больше или равно. == - равенство. Условие верно, если два операнда равны. != - неравенство. Условие верно, если два операнда неравны. Например, условие (x * x < 1000) означает “значение x * x меньше 1000”, а условие (2 * x != y) означает “удвоенное значение переменной x не равно значению переменной y”. Операторы сравнения в Питоне можно объединять в цепочки (в отличии от большинства других языков программирования, где для этого нужно использовать логические связки), например, a == b == c или 1 <= x <= 10. Виды используемых циклов. 1.Цикл while (“пока”). Позволяет выполнить одну и ту же последовательность действий, пока проверяемое условие истинно. Условие записывается до тела цикла и проверяется до выполнения тела цикла. Как правило, цикл while используется, когда невозможно определить точное значение количества проходов исполнения цикла. 2.Цикл for, также называемый циклом с параметром, в языке Питон богат возможностями. В цикле for указывается переменная и множество значений, по которому будет пробегать переменная. Множество значений может быть задано списком, кортежем, строкой или диапазоном (будет рассматриваться в следующей лабораторной работе). Пример. Вывод таблицы значений функцииПостановка. Вывести таблицу значений заданной функции на отрезке и с шагом, которые вводит пользователь. Пусть функция будет такой: y = -3x2 - 4x + 20. Метод решения. Запросить у пользователя точки начала и конца отрезка, а также шаг. Если значение точки начала отрезка больше значения точки конца, то поменять значения. Пока значение первой точки не достигнет второй вычислить значение функции, вывести на экран текущие значения x и y, увеличить значение первой точки на шаг. Реализация на Python 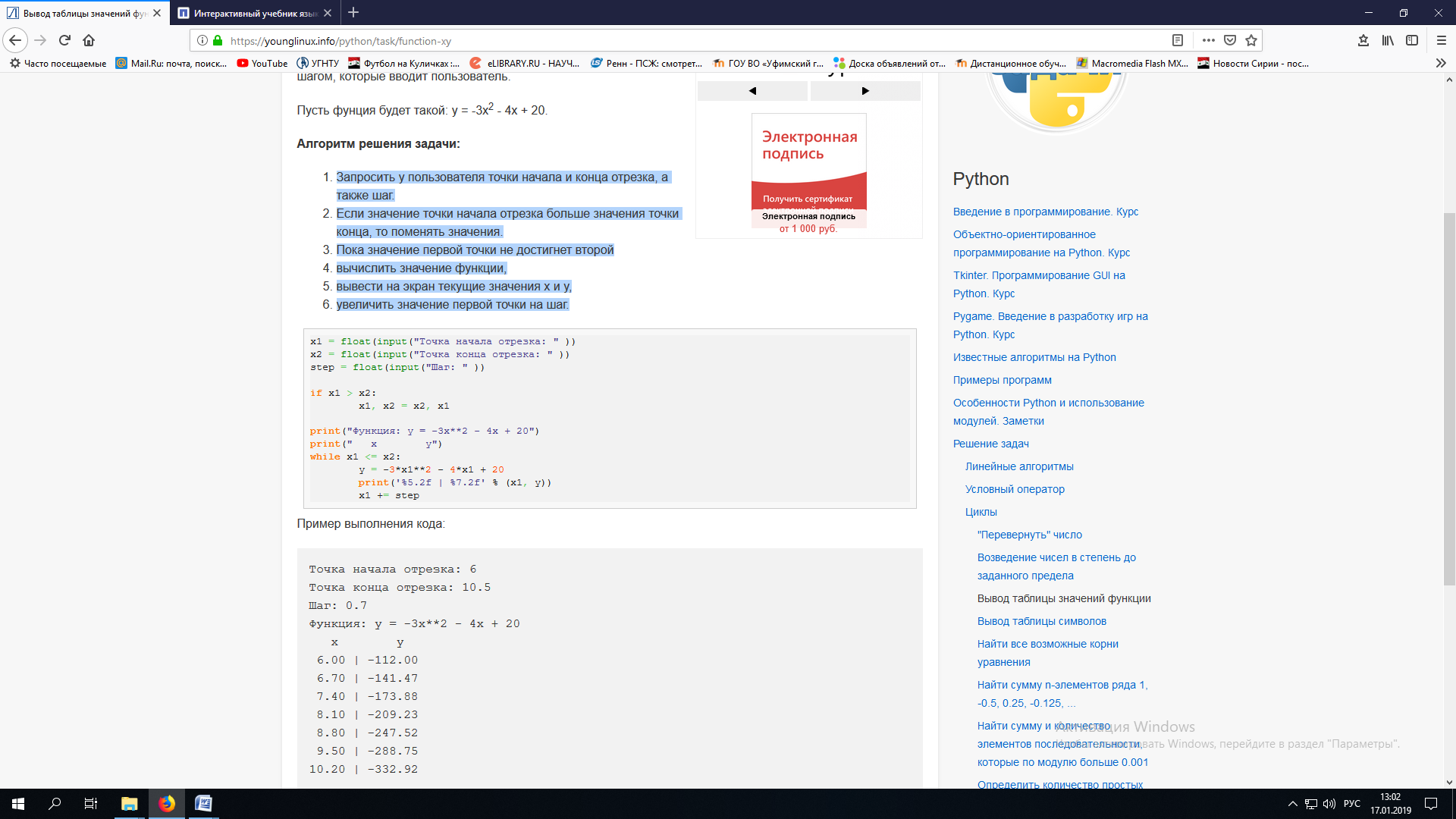 Проверка результата: Точка начала отрезка: 6 Точка конца отрезка: 10.5 Шаг: 0.7 Функция: y = -3x**2 - 4x + 20 x y 6.00 | -112.00 6.70 | -141.47 7.40 | -173.88 8.10 | -209.23 8.80 | -247.52 9.50 | -288.75 10.20 | -332.92 Здесь использовались форматы вывода: 1.3 Пример выполнения лабораторной работы Задание 1. Составить программу линейного алгоритма для вычисления значения: 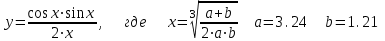 Составляем программу: 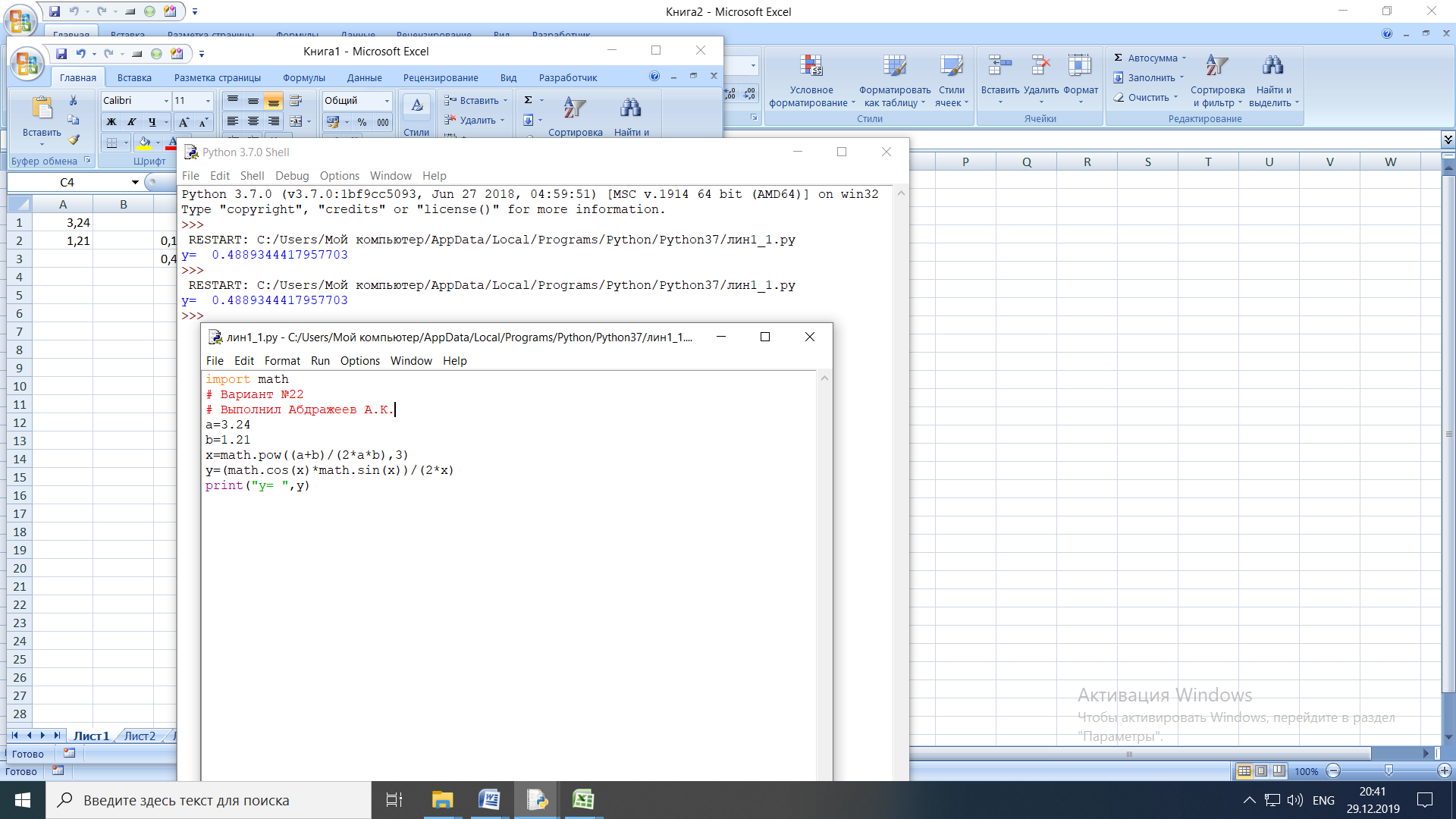 Результат:  Примечание. В комментариях следует указать автора, т.е. кто выполнил (свою фамилию и номер группы), а также все переменные. В случае если по каким-либо причинам не укажете, то оценка за работу будет снижена. Задание 2. Составить программу разветвляющего алгоритма вычисления значения: 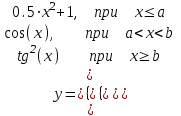 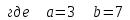 Составляем программу: 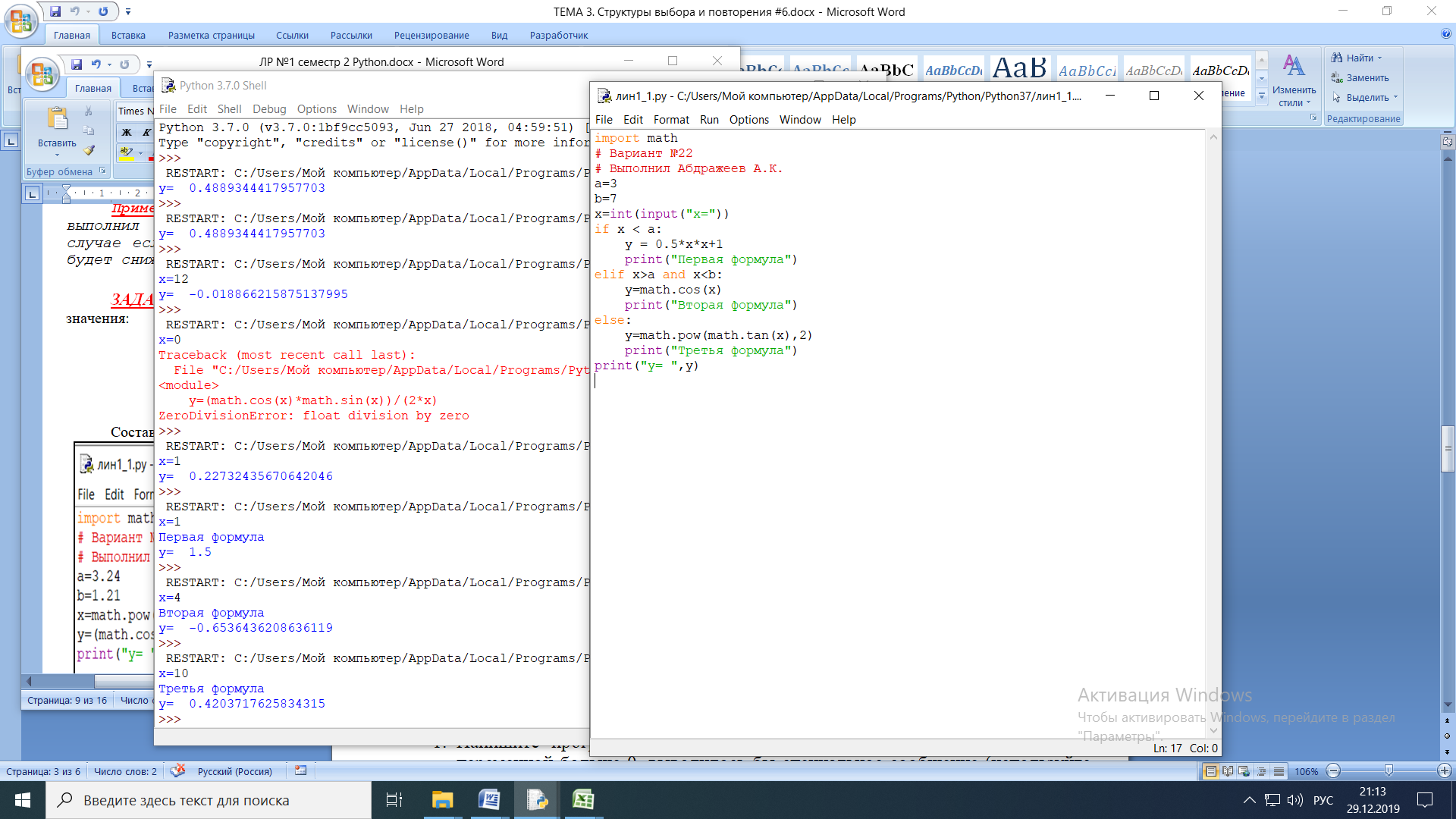 Результат:  Задание 3. Пример 3. Составить программу нахождения суммы следующего выражения: 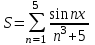 где x - любое не равное нулю и единице число где x - любое не равное нулю и единице числоСоставляем программу: 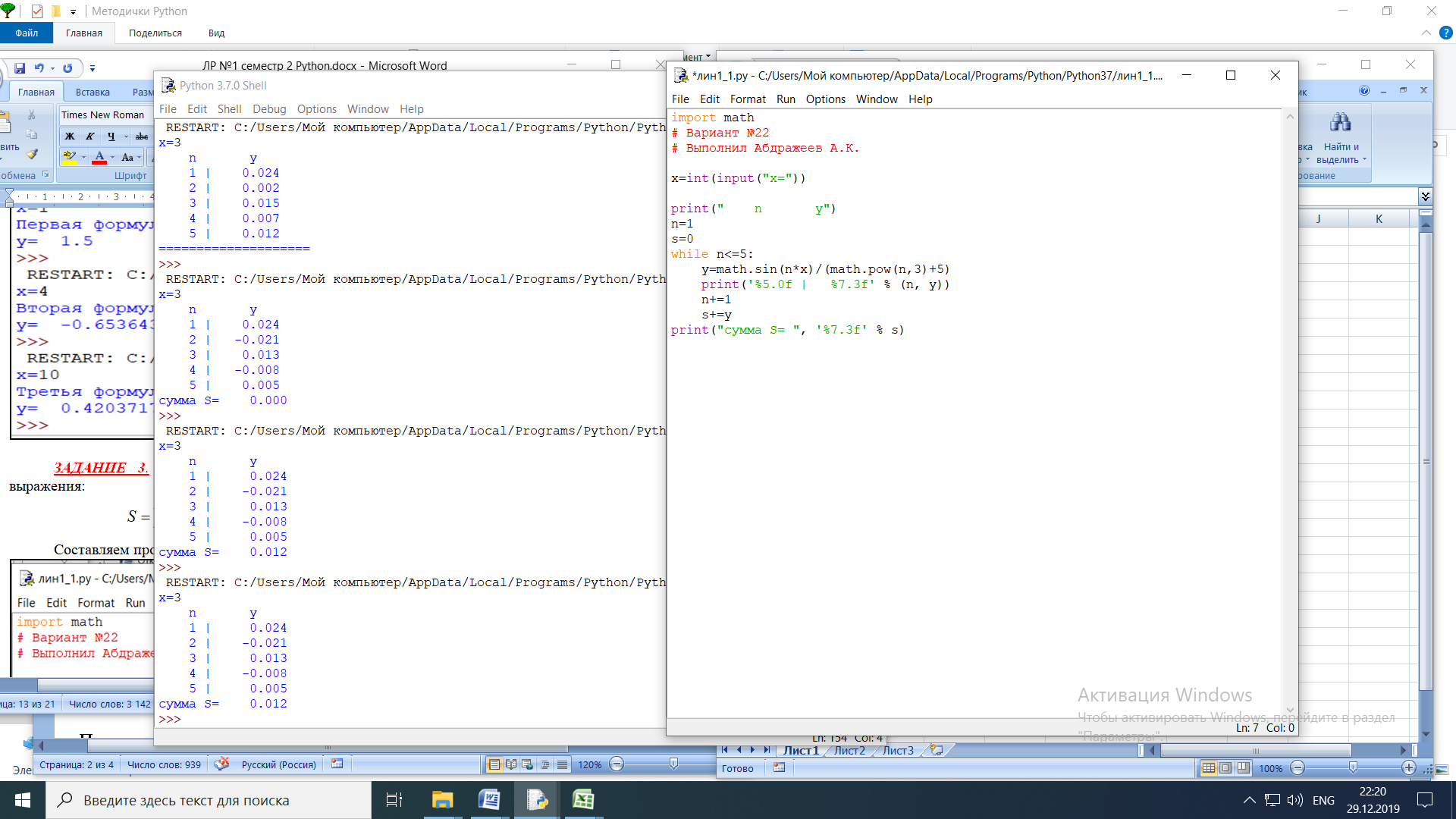 Результат:  1.4 варианты для выполнения лабораторной работы Задание №1: Разработайте линейный алгоритм и представьте его в графическом виде (блок-схемы). Вычислить значение выражения s при заданных исходных данных. Указание. Для упрощения выражений можно ввести промежуточные переменные.
Задание №2: Разработайте алгоритм разветвляющего процесса и представьте его в графическом виде (блок-схемы). Вычислить значение выражения y при заданных исходных данных. Указание. Для упрощения выражений можно ввести промежуточные переменные.
Задание №3: Разработайте циклический алгоритм вычисления суммы 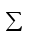 (произведения (произведения 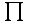 ) конечного числа элементов ряда и представьте его в графическом виде (блок-схемы). ) конечного числа элементов ряда и представьте его в графическом виде (блок-схемы). Вычислить значение выражения при заданных исходных данных.
ПРИЛОЖЕНИЕ 1. Функционал модуля Math math.ceil(X) – округление до ближайшего большего числа. math.copysign(X, Y) - возвращает число, имеющее модуль такой же, как и у числа X, а знак - как у числа Y. math.fabs(X) - модуль X. math.factorial(X) - факториал числа X. math.floor(X) - округление вниз. math.fmod(X, Y) - остаток от деления X на Y. math.frexp(X) - возвращает мантиссу и экспоненту числа. math.ldexp(X, I) - X * 2i. Функция, обратная функции math.frexp(). math.fsum(последовательность) - сумма всех членов последовательности. Эквивалент встроенной функции sum(), но math.fsum() более точна для чисел с плавающей точкой. math.isfinite(X) - является ли X числом. math.isinf(X) - является ли X бесконечностью. math.isnan(X) - является ли X NaN (Not a Number - не число). math.modf(X) - возвращает дробную и целую часть числа X. Оба числа имеют тот же знак, что и X. math.trunc(X) - усекает значение X до целого. math.exp(X) - eX. math.expm1(X) - eX - 1. При X → 0 точнее, чем math.exp(X)-1. math.log(X, [base]) - логарифм X по основанию base. Если base не указан, вычисляется натуральный логарифм. math.log1p(X) - натуральный логарифм (1 + X). При X → 0 точнее, чем math.log(1+X). math.log10(X) - логарифм X по основанию 10. math.log2(X) - логарифм X по основанию 2. math.pow(X, Y) - XY. math.sqrt(X) - квадратный корень из X. math.acos(X) - арккосинус X. В радианах. math.asin(X) - арксинус X. В радианах. math.atan(X) - арктангенс X. В радианах. math.atan2(Y, X) - арктангенс Y/X. В радианах. С учетом четверти, в которой находится точка (X, Y). math.cos(X) - косинус X (X указывается в радианах). math.sin(X) - синус X (X указывается в радианах). math.tan(X) - тангенс X (X указывается в радианах). math.hypot(X, Y) - вычисляет гипотенузу треугольника с катетами X и Y (math.sqrt(x * x + y * y)). math.degrees(X) - конвертирует радианы в градусы. math.radians(X) - конвертирует градусы в радианы. math.cosh(X) - вычисляет гиперболический косинус. math.sinh(X) - вычисляет гиперболический синус. math.tanh(X) - вычисляет гиперболический тангенс. math.acosh(X) - вычисляет обратный гиперболический косинус. math.asinh(X) - вычисляет обратный гиперболический синус. math.atanh(X) - вычисляет обратный гиперболический тангенс. math.erf(X) - функция ошибок. math.erfc(X) - дополнительная функция ошибок (1 - math.erf(X)). math.gamma(X) - гамма-функция X. math.lgamma(X) - натуральный логарифм гамма-функции X. math.pi - pi = 3,1415926... math.e - e = 2,718281... |