механика жидкости и газа. Механика жидкости и газа. Лабораторная работа по дисциплине (учебному курсу)

Название	Лабораторная работа по дисциплине (учебному курсу)
Анкор	механика жидкости и газа
Дата	22.02.2023
Размер	0.62 Mb.
Формат файла
Имя файла	Механика жидкости и газа.docx
Тип	Лабораторная работа #950616
страница	1 из 4

1 2 3 4

МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
федеральное государственное бюджетное образовательное учреждение

высшего образования
«Тольяттинский государственный университет»

(наименование института полностью)
Кафедра /департамент /центр¹ __________________________________________________

(наименование кафедры/департамента/центра полностью)

ЛАБОРАТОРНАЯ РАБОТА №___
по дисциплине (учебному курсу) «___________________________________»

^{(наименование дисциплины (учебного курса)}
Вариант ____ (при наличии)

Студент	(И.О. Фамилия)
Группа
Преподаватель	(И.О. Фамилия)

Тольятти 20__

Практическое задание для допуска к виртуальным лабораторным работам

УРАВНЕНИЕ Д. БЕРНУЛЛИ

(экспериментальное изучение и практическая реализация)

Цель работы: ознакомиться и понять смысл уравнения Бернулли, уметь применять его для решения практических задач гидродинамики.

Схема лабораторной установки

Работа производится на установке, представленной на рис. 1.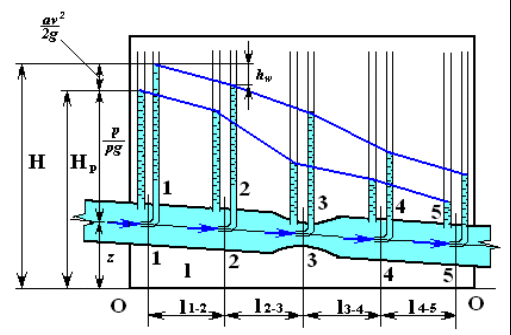

Рис. 1. Экспериментальная установка и построение линий полного и пьезометрического напоров при течении жидкости в трубе переменного сечения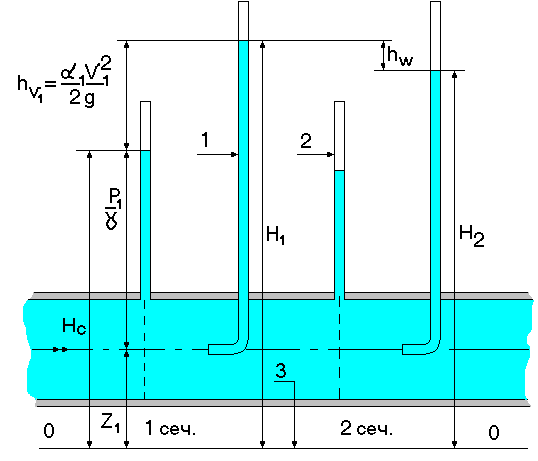

Рис. 2. Пример геометрической интерпретации уравнения Бернулли

Закон сохранения энергии для установившегося потока несжимаемой жидкости в поле сил тяжести выражается уравнением Бернулли:

Z₁ + P₁/γ + α₁υ₁²/(2g) = Z₂ + P₂/γ + α₂υ₂²/(2g) + h_w. (1)

Уравнение (1) можно записать в виде

Z₁g + P₁g/γ + α₁υ₂²/2 = Z₂g + P₂g/γ + α₂υ₂²/2 + h_wg. (2)

Все величины, входящие в уравнения (1) и (2), имеют геометрический и энергетический смыслы (табл. 1, рис. 2).

Таблица 1

Величина	Энергетический смысл	Величина	Геометрический смысл
Zg	Удельная потенциальная энергия положения	Z	Геометрическая высота от плоскости сравнения до центра тяжести сечения потока (геометрический напор)
Pg/γ	Удельная потенциальная энергия давления	P/γ	Пьезометрическая высота, замеряемая от центра тяжести сечения до уровня жидкости в пьезометре (пьезометрический напор)
αυ²/2	Удельная кинетическая энергия	αυ²/(2g)	Скоростная высота, замеряемая по разности высот в пьезометре и трубке Пито (скоростной напор)
Zg + Pg/γ + αυ²/2	Полная удельная энергия	H = Z+ P/γ + αυ²/(2g)	Гидродинамический напор (полный напор)
h_wg	Потеря энергии между рассматриваемыми сечениями	h_w	Потеря напора, замеряемая по разности полных напоров в двух сечениях

Результаты измерений и расчетов

Таблица 2

№

сеч.

l – длины меду сечениями, см

Z, геометрический напор, см

Нс статический напор, см

H – полный напор, см

h_w, потерь напора, см

h_v_{- -}скоростной напор, см

V, скорость, см/с

Уклоны

i – геометрический

J_p – пьезометрический

J – гидравлический

30,7

8,8

4,22

0,073

0,130

6,55

4,22

24,7

4,5

0,074

1,336

0,182

4,73

50.5

29,5

22,94

22,7

20,5

0,074

-0,374

0,903

3,06

29.5

0,5

2,99

30,8

0,073

0,032

0,8

28.5

0,5

2,99

Построение графика зависимости напоров от изменений длины между сечениями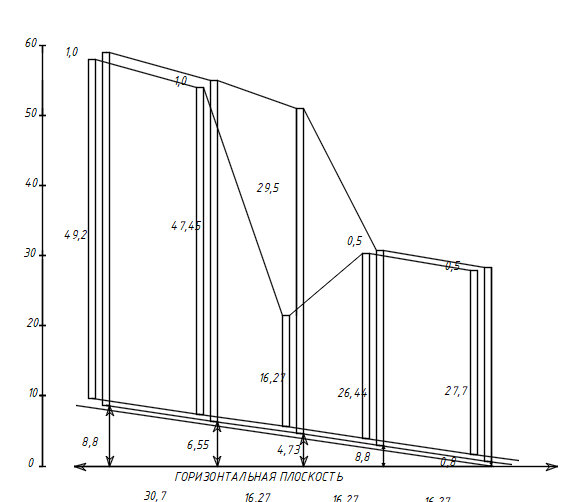

Рис. 1. Графики зависимости напоров от изменении длины трубопровода наклонного расположения (на оси OY размесщены напоры (Z, Н_{статический} = Z+ P / γ; H_{полный )}; на оси OX – длины между сечениями)

Вывод: в данной работе мы ознакомились с уравнением Бернулли, научились вычислять слагаемые уравнения и построили графики зависимости напоров от длины трубопровода.

1 2 3 4