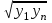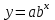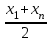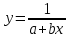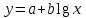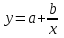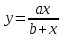ЛР_7-222. Лабораторная работа Расчётная часть. Построение модели нелинейной регрессии по несгруппированным данным

• Название: Лабораторная работа Расчётная часть. Построение модели нелинейной регрессии по несгруппированным данным
• Дата: 10.04.2022
• Размер: 485.08 Kb.
• Имя файла: ЛР_7-222.docx
• Тип: Лабораторная работа; #458273

Лабораторная работа № 7.2.

Расчётная часть.

Построение модели НЕлинейной регрессии по несгруппированным данным.

Условие: по имеющимся исходным данным:

1. 
   Определить вид регрессии.
   
2. 
   Вычислить числовые характеристики , , s_x, s_y, i.
   
3. 
   Найти эмпирическое уравнение регрессий Y на X.
   
4. 
   Вычислить коэффициент детерминации R² и объяснить его смысловое значение.
   
5. 
   Проверить адекватность уравнения регрессии Y на X.
   

Пример

X	1,596	2,429	2,429	2,464	2,465	2,89	2,9
Y	9	15,5	14	15,8	16,5	15,4	15,1

Расчет:

1. 
   Найдем вид уравнения регрессии методом средних точек.
   

Необходимо выбрать формулу, которая могла бы описать экспериментальные данные. В таблице 12 приведены типовые формулы.
Таблица 12

№	Формула	Средние точки
1
2
3
4
5
6

Нанесем на график 6 исходные данные и соединим соседние точки отрезками прямых. На этот же график нанесем средние точки для каждой кривой.

График 6



Рассчитаем значение коэффициентов уравнения регрессии.

(2.38)

Сделаем замену y=g , a=c₀ , b=c₁ , .

Коэффициенты (параметры) c₀иc₁ находят методом наименьших квадратов. Сведем задачу к решению системы нормальных уравнений:

(2.39)

(2.40)

В MS Excel составили таблицу 13:

Таблица 13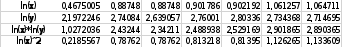



Подставим полученные данные в нашу систему уравнений:



Решая ее, получаем c₀=1,49803922,c₁=1,31372549. x.

Проведем исследование на адекватность.

Составим таблицу 14:

Таблица 14


На график 6 нанесем график полученной кривой (график 7):
График 7



Найдем коэффициент детерминации: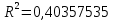


Большое значение коэффициента детерминации говорит о том, что практически весь разброс значений величины y объясняется линейной корреляционной зависимостью.

Проверим гипотезу об адекватности полученной сглаживающей кривой исходными данными по критерию Фишера при уровне значимости α=0,05

((2.41)

По числу степеней свободы k₁=1 и k₂=n-2=6 найдем критическое значение F_кр=6,60789097.

Так как F_выб F_кр, делаем вывод о том, что полученное уравнение экспоненциальной регрессии статистически значимо описывает результат эксперимента. Гипотезу об адекватности полученной сглаживающей прямой принимаем.

Найдем тесноту связи между X и Y с помощью индекса корреляции.

(2.42)

Характер связи – сильный.
Вариант №1.

X	21,07	23,07	28,69	22,42	21,41	18,49	21,64	39,19	51,96	42,36	51,80	50,45
	50,6	40,0	29,6	32,5	34,9	47,6	42,0	18,7	12,5	20,1	15,1	15,2

Вариант № 2.

X	5	6	8	13	34	72	95	113	127	90
Y	143	125	87	45	33	27	16	25	24	27

Вариант№3.

v	1	1,2	1,7	2,4	3,6	4,7	6	8	11	14
S	26	22	22,6	19,1	15,2	12,8	11,3	9,5	7,8	6,5

Вариант № 4.

Pc	1	3	5	7	9	11	13	15	17
S	12,5	17,8	37	41,9	45	47	39	32	28

Вариант № 5.

K	1,5	2,5	3,5	4,5	5,5	6,5
v0	1,2	0,6	0,21	0,9	1,4	1,9

Вариант № 6.

X	1	2	4	9	13	18	20
Y	26	22	19	12	9	8	6

Вариант №7.

X	1	2	3	4	5	6	7
Y	5	3,33	2,9	2,2	2,1	2	2

Вариант № 8.

Pc	1	3	5	7	9	11	13	15
My	22,5	11,5	6	5,5	2,6	2,4	2,1	2

Вариант № 9.

KВ	0,25	0,35	0,45	0,55	0,65	0,75	0,85
SН	0,65	0,45	0,25	0,15	0,10	0,05	0,07

Вариант № 10.

X	5	10	15	20	25
Y	12,1	29,3	36	42	45

Вариант № 11.

X	73	75	79	82	83	86	80	85	95	93	97	77
Y	14	21	29	30	31	35	34	41	38	39	46	27

Вариант № 12.

P	2,23	3,28	4,65	6,5	8,1
v	0,3	0,6	1,2	2,4	4,2

Вариант № 13.

X	0,5	1,0	2,0	3,0	4,0	5,0	6,0
Y	290	250	216	206	200	195	190

Вариант № 14.

X	0,5	1,5	2,5	3,5	4,5	5,5	7,5
Y	15	11	12	10,8	10	9	8

Вариант № 15.

X	1,5	2,9	3	3,1	3,2	3,4	3,5	3,6	4,2
Y	580	618	658	670	662	699	717	775	786

Вариант № 16.

X	0,1	0,4	1	4	6	10	20	26
Y	2248	1950	1500	1020	906	290	175	121

Вариант № 17.

Q	5	15	25	35	45	55
P	1,25	1,3	5,25	11,25	17,25	21,25

Вариант № 18.

X	1	1,5	2,5	3,5	4,5	5,5	6,5
Y	4	6	6,8	7,9	8,7	9	9,5

Вариант № 19.

X	1	3	5	7	9	11	13	15	17
Y	25	15	12	8	10	5	4,5	3	2,8

Вариант № 20.

X	1	2	3	4	5	6
Y	1,2	2,6	3,8	4,6	4,9	5,4

Вариант № 21.

X	21	24	30	34	35	36	39	40
Y	20	13	12	13	11	10	11	10

Вариант № 22.

X	3	3,05	3,6	4,25	4,45	4,55
Y	1	1,5	1,8	2,5	3	4

Вариант № 23.

X	1	4	7	9	11	12	15
Y	10	12	26	30	40	42	58

Вариант № 24.

X	1	2	3	4	5	6	7	8
Y	0,9	2,59	3,67	4,45	4,95	5,20	4,7	4,5

Вариант 25.

X	50	100	150	200	250	300
Y	140	120	118	110	115	100

Вариант № 26.

P0	12,5	37,5	62,5	87,5	112,5	137,5	187,5
V	0,19	0,13	0,11	0,10	0,08	0,07	0,06

Вариант № 27.

t	0,025	0,074	0,125	0,175	0,225	0,275	0,325
P	95	73	52	45	35	33	31

Вариант № 28.

X	1	2	3	4	5	6	7
Y	0,8	1,2	1,8	2,9	4,2	5,9	12,5

Вариант № 29.

X	0,5	1,5	2,5	3,5	4,5	6,0	9	10
Y	14	11	10	8	6,5	5	4,5	4

Вариант№30.



Вариант №31.

X	1,5	2,5	3,5	4,5	5,5	6,0	8	11
Y	140	100	100	80	67	49	45	30

Вариант №32.

X	11	13	14	15	16	17	18
Y	1,8	2,2	2,8	2,9	4,5	6,9	12,5

Варианты №33.

X	1,596	2,429	2,429	2,464	2,465	2,89	2,9
Y	9	15,5	14	15,8	16,5	15,4	15,1

Вариант №34.

X	3,5	3,45	3,7	4,75	5,45	5,55
Y	10	15	18	24	30	34

Вариант №35.

X	4	8	16	20	21	23	25
Y	12,1	29,3	36,2	42,4	40,1	50,1	45,6

Вариант №36.

X	1	3	6	9	13	14	15
Y	10	13	20	32	40	38	58

Вариант №37.

X	21	24	30	31	34	36	38	40
Y	800	900	1100	1300	1400	1500	1560	2000

Вариант № 38.

X	70	75	80	82	84	86	87	90	95	93	97	99
Y	14	21	22	30	31	35	34	41	38	39	46	44