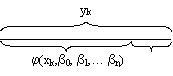|
|
Экономико-математическое моделирование - случайные величины. LAB 01 Случайные величины, их статистические характеристики. Лабораторная работа случайные величины, их статистические характеристики
1.1. Экономическая модель
Основным элементом экономического исследования является анализ и построение взаимосвязей экономических переменных. Математическое выражение таких взаимосвязей называется экономической моделью.
Пример.
С = 0 + 1I,
I – располагаемый доход семьи;
C – потребление.
Построение экономических моделей осложнено следующими факторами
часто эти взаимосвязи не являются строгими, функциональными зависимостями;
очень трудно выявлять все факторы, влияющие на данный зависимый экономический показатель;
воздействие многих факторов является случайным;
экономисты обладают ограниченным набором данных статистических наблюдений, которые к тому же содержат различного рода ошибки.
Если удаётся преодолеть эти трудности, тогда можно построить экономическую модель, выражающую функциональную зависимость некоторой зависимой величины от формирующих её значение факторов. Особенность функциональной зависимости состоит в том, что по значению независимой величины (переменной) можно однозначно, абсолютно точно вычислить, предсказать значение зависимой величины.
Рассмотрим набор реальных статистических данных (Ck,Ik) и изобразим эти данные точками в координатах (C,I).

Таким образом, зависимость между величинами Ck, Ik не функциональная, а стохастическая, случайная. Но эта случайность не такова, что абсолютно невозможно предсказать или объяснить по величине Ik величину Ck, поскольку видна достаточно устойчивая тенденция роста (в среднем). Другими словами, взаимосвязь между величинами Ck, Ik такова: точное значение Ck не вычисляется по значению Ik, однако с ростом Ik значение Ck в среднем увеличивается. Такой характер зависимости выражается следующим образом:
Ck = 0 + 1Ik + k, k = 1, 2,…,N (1)
В общем случае, характер зависимости нелинейный:
yk = (xk,0, 1,… n) + k; k = 1, 2,…,N (2).
Соотношение (2) называется эконометрической моделью. Таким образом, эконометрическая модель – это выражение статистической зависимости между переменными. Эконометрическая модель строится на основе экономической теории и статистических данных.
1.2. Элементы эконометрической модели и их свойства
Вид функции называется спецификацией модели. Модель (1) является частным видом эконометрической модели, в которой спецификация линейная. Функция описывает общий ход экономического процесса, экономическую тенденцию развития, изменения зависимого показателя при изменении независимого.
Величина x – называется независимой или объясняющей переменной;
Величина y называется зависимой или объясняемой переменной. Значение величины yk состоит из двух частей:
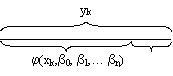
величина (xk,0, 1,… n) – это часть зависимого показателя, обусловленная или объяснённая экономическими причинами или просто объясняемая часть; k – необъяснённая часть, поскольку невозможно описать все случайные факторы.
k – величина, выражающая вклад случайных мелких, незначительных факторов, которые отклоняют реальные статистические данные от значений зависимого показателя, обусловленного экономической тенденцией, однако не изменяют эту экономическую тенденцию.
Основные свойства величин k:
1) эти величины случайные, в противном случае зависимость (2) функциональная;
2) k принимают положительные и отрицательные значения, так как случайные факторы увеличивают или уменьшают величины, обусловленные экономической тенденцией;
3) Абсолютные величины |k| не должны быть очень большими по сравнению со значениями, вычисляемыми по спецификации. Другими словами, необъяснённая часть показателя y должна быть мала по сравнению с объяснённой. Если же отклонения значительны, тогда спецификация неточно описывает экономическую тенденцию, её необходимо уточнять и в число объясняющих факторов вводить факторы, вклад которых приводит к большим значениям k.
0, 1,…, k – параметры спецификации. Для разных видов функции количество этих параметров, их смысл и названия разные. Например, для линейной спецификации
yk = 0 + 1xk + k; k = 1, 2,…,N
этих параметров два;
параметр
0 – свободный член,
1 – угловой коэффициент.
1.3. Случайные величины. 1.3.1. Цель работы
Научиться формировать в MSExcel последовательности случайных чисел с заданными статистическими характеристиками. Это необходимо для моделирования экономических объектов, имеющих случайную природу, и последующего эконометрического анализа поведения моделей таких объектов.
1.3.2. Генерация случайных чисел
Последовательности случайных чисел формируются двумя способами:
вызов диалогового окна «Генерация случайных чисел».
непосредственное использование функций СЛЧИС(), СЛУЧМЕЖДУ().
Рассмотрим оба этих способа.
1.3.3. Диалоговое окно "Генерация случайных чисел"
Это окно вызывается последовательностью
Сервис/Анализ данных/Генерация случайных чисел
и выглядит следующим образом:

Диалоговое окно "Генерация случайных чисел"
Число переменных
Здесь следует ввести количество последовательностей случайных чисел (последовательность представляет одну случайную переменную). Каждая последовательность располагается в столбце. Если это значение не задать, то каждый столбец в выходном диапазоне (который будет задан в рамке Параметры вывода) будет заполнен последовательностью случайных чисел. Если формируется одна последовательность, то следует ввести 1.
Число случайных чисел
Введите число случайных чисел в последовательности. Это число будет определять высоту столбцов выходного диапазона. Если число случайных чисел не будет введено, то все строки выходного диапазона будут заполнены.
Распределение
Выберите распределение, которое необходимо использовать для генерации случайных переменных. Ограничимся только равномерным распределением.
Равномерное
Характеризуется верхней и нижней границами интервала. Переменные извлекаются с одной и той же вероятностью для всех значений интервала.
Параметры
Здесь следует задать нижнюю и верхнюю границы интервала. Равномерно распределённые числа принимают значения между границами интервала.
Выходной интервал
Введите ссылку на левую верхнюю ячейку выходного диапазона. Размер выходного диапазона будет определен автоматически, и на экран будет выведено сообщение в случае возможного наложения выходного диапазона на исходные данные. Может быть задана нижняя правая ячейка интервала.
Новый лист
Установите переключатель, чтобы открыть новый лист в книге и вставить результаты анализа, начиная с ячейки A1. Если в этом есть необходимость, введите имя нового листа в поле, расположенном напротив соответствующего положения переключателя.
Новая книга
Установите переключатель, чтобы открыть новую книгу и вставить результаты анализа в ячейку A1 на первом листе в этой книге.
Пример
После ввода данных, приведённых на рисРис. 1. будут получены следующие результаты

Последовательности случайных чисел
1.3.4. Использование функций СЛЧИС(), СЛУЧМЕЖДУ()
Функция СЛЧИС() равновероятно формирует вещественное случайное число между 0 и 1. Эта функция не имеет аргументов. Для создания последовательности таких чисел нужно выполнить следующее:
ввести в ячейку функцию СЛЧИС(), выделить эту ячейку;
подвести курсор к чёрному квадратику в правом нижнем углу ячейки (рисРис. 3.), и, когда курсор примет форму чёрного крестика, потянуть его вправо (влево, вверх, вниз) с нажатой левой клавишей мыши (рисРис. 4.);

Использование функции СЛЧИС()
потянув чёрный квадрат строки (рисРис. 4.) случайных чисел вниз(вверх), можно получить несколько последовательностей случайных чисел.
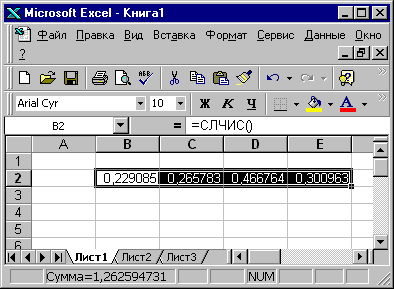
Случайная последовательность
Функция СЛУЧМЕЖДУ(нижн_граница;верхн_граница) равновероятно возвращает случайное целое число между заданными границами.
Нижн_граница - это наименьшее целое число, которое возвращает функция СЛУЧМЕЖДУ.
Верхн_граница - это наибольшее целое число, которое возвращает функция СЛУЧМЕЖДУ.
Необходимо, чтобы нижн_граница верхн_граница.
Каждый раз, когда рабочий лист перевычисляется, возвращается новое случайное число.
Для получения вещественных случайных чисел в диапазоне от 0 до N следует использовать произведение СЛЧИС()*N.
1.4. Вычисление среднего значения, дисперсии и стандартного отклонения случайной
Функция СРЗНАЧ(Диапазон) вычисляет среднее значение чисел в указанном диапазоне. Обозначим это значение Х.
Функция ДИСП(Диапазон) вычисляет среднее значение квадрата отклонения от Х.
Функция СТАНДОТКЛОН(Диапазон) вычисляет корень квадратный из среднего значения квадрата отклонения от Х.
1.4.1. Выполнение лабораторной работы
Разобрать приведённый пример.
Используя диалоговое окно "Генерация случайных чисел" и непосредственный ввод в ячейки функций СЛЧИС(), СЛУЧМЕЖДУ(), сформировать случайные последовательности случайных чисел с заданным диапазоном и в заданном месте таблицы.
Вариант
|
Интервал случайной величины
|
Количество последовательностей
|
Количество чисел в последовательности
|
|
вещественные (0; 6,5)
|
3
|
6
|
|
целые [-10;20]
|
5
|
7
|
|
вещественные (0;16,75)
|
2
|
6
|
|
целые [-9;2]
|
4
|
5
|
|
вещественные (0; 5,25)
|
3
|
6
|
|
вещественные (-10,5;0)
|
4
|
5
|
|
целые [-8;13]
|
2
|
6
|
|
вещественные (-5,9;0)
|
4
|
5
|
|
целые [-7;5]
|
6
|
6
|
|
вещественные (-25; 0)
|
5
|
6
|
Вычислить среднее значение, дисперсию и стандартное отклонение для введённого массива случайных чисел.
Контрольные вопросы:
Что такое случайная величина?
Что такое дискретная случайная величина?
Что такое непрерывная случайная величина?
Что такое математическое ожидание? Дисперсия? Среднеквадратическое отклонение?
Что такое экономическая модель?
В чем состоят трудности построения экономических моделей?
Что такое эконометрическая модель?
Перечислить элементы эконометрической модели и их свойства?
Дать определение дисциплины Эконометрика?
Перечислить этапы эконометрического моделирования?
Дать классификацию эконометрических моделей?
|
|
|
 Скачать 89 Kb.
Скачать 89 Kb.