Лабораторная работа Сплайновые кривые Цель работы
 Скачать 1.53 Mb.
|
|
Лабораторная работа № 1. Сплайновые кривыеЦель работы Изучение способов описания элементарных сплайновых кривых и получение практических навыков построения составных и рациональных сплайновых кривых. 2. Теоретические положения По заданному множеству вершин  с учетом их нумерации необходимо построить гладкую кривую, которая, плавно меняясь, последовательно проходила бы в близости этих вершин и удовлетворяла бы некоторым дополнительным условиям. При отыскании подходящего решения задачи приближения важную роль играет ломанная, звенья которой последовательно соединяют рассматриваемые вершины заданного набора. Эту ломанную называют контрольной, а ее вершины – контрольными. Ограничение на множество вершин не накладывается: вершины могут располагаться как на плоскости, так и в пространстве, их взаимное расположение может быть произвольным; некоторые вершины могут и совпадать. Поэтому описание кривой ищется в параметрическом виде:  ,где  - весовая функцияДля решения задачи приближения успешно применяются кривые, составленные из элементарных фрагментов. В случае, когда элементарные фрагменты строятся по сравнительно простой схеме, такие составные кривые принято называть сплайновыми кривыми. Наибольшее распространение получили методы конструирования составных кривых, в которых используются кубические многочлены, что позволяет учесть и дифференциальные и внешне геометрические требования, накладываемые на искомую кривую. На рисунке 3.1. приведены способы задания четырех векторов для определения элементарной кубической кривой. 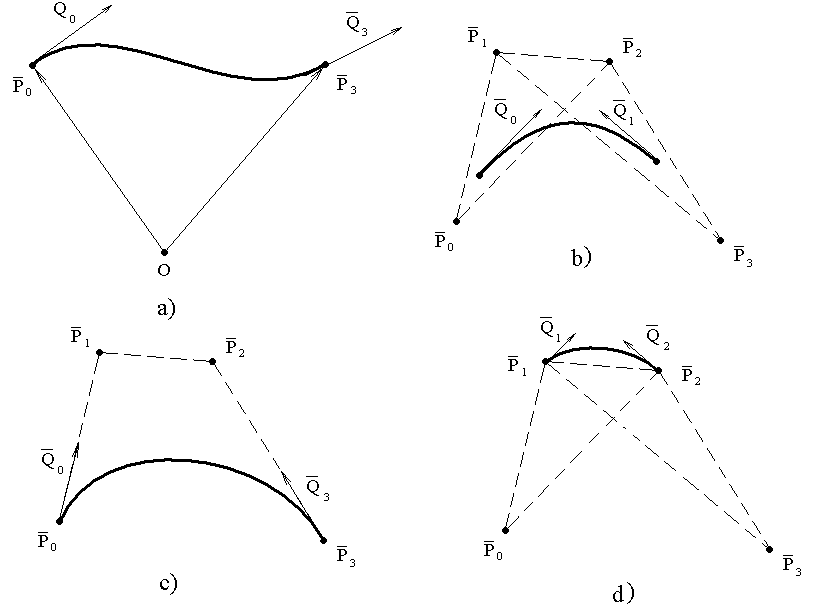 Рис. 3.1. а) элементарная кривая Эрмита, b) элементарный В-сплайн, с) элементарная кривая Безье, d) элементарная кривая Catmull-Rom. Элементарная кубическая кривая Безье описывается уравнением вида:  Элементарная В–сплайновая кривая описывается уравнением вида:     Элементарная кривая Эрмита описывается уравнением вида:  Элементарная кривая Catmull-Rom описывается уравнение вида:     Построив кривую, ее можно подвергнуть аффинному преобразованию. Можно поступить по другому: сначала подвергнуть преобразованию заданный набор опорных вершин, только потом построить кривую. Если результат окажется одинаковым, то говорят, что кривая инвариантна относительно этого преобразования. Большинство из рассматриваемых классов кривых обладает свойством аффинной инвариантности. Использование рациональных кривых, которые являются проективно инвариантными, вносит в решение задачи приближения нужную гибкость. 4. Задание на работу Получить вариант задания у преподавателя. 5. Порядок выполнения работы 5.1. Ознакомиться с теоретическими положениями, 5.2. Построить сплайновую кривую по заданному массиву точек. 6. Оформление отчета Отчет должен содержать: цель работы, задание на работу, текст отлаженной программы, результаты работы программы. 7. Контрольные вопросы 7.1. Что представляет собой сплайн? 7.2. Что представляет собой опорная ломанная? 7.3. Дайте определение аффинной инвариантности. 7.4. Какими свойствами обладает сплайн Безье? |