отчет 4-. Лабораторная работа Управление в пространстве состояний. Цель работы Изучить модальное управление
 Скачать 497 Kb. Скачать 497 Kb.
|
|
М  инистерство образования РТ инистерство образования РТАльметьевский государственный нефтяной институт Кафедра АИТ ОТЧЕТ По лабораторным работам №4 По дисциплине «Проектирование автоматизированных систем» Альметьевск 2013 Лабораторная работа № 4 .Управление в пространстве состояний. Цель работы: Изучить модальное управление. Управление в пространстве состояний Размеры задачи Программа запрашивает размеры трех векторов: вектора состояния x ([x]=n), вектора управления u ([u]=r) и вектора выхода y ([y]=m). Размеры остальных векторов и матриц определяются этими тремя: матрица A имеет размеры nxn, B - размеры nxr, C - размеры mxn, и т.д. Ограничения: n не больше 10, r и m не больше n. Установленные размеры задачи не меняются до конца работы программы. Выбор задачи В программе заложено четыре варианта задачи: 1) детерминированная система, модальное управление (DM), 2) детерминированная система, оптимальное управление (DO), 3) стохастическая система, модальное управление (SM), 4) стохастическая система, оптимальное управление (SO). Вариант указан на схеме в правом нижнем углу. В стохастическом варианте на систему воздействуют случайные помехи w и v, в детерминированном варианте помехи не учитываются. В варианте "оптимальное управление" матрица регулятора R вычисляется из условия минимума квадратичного критерия качества, в "модальном управлении" матрица R находится так, чтобы замкнутая система A-BR имела заданный характеристический многочлен. При вычислении R подсистема наблюдения не учитывается. Матрица K в детерминированном варианте находится из условия заданного качества матрицы A-KC, а в стохастическом варианте - из условия наилучшего подавления помех (фильтр Калмана). Проверка чувствительности Предполагается, что матрица A, которая используется для расчета регулятора и наблюдателя (фильтра), является матрицей объекта лишь приближенно, а в точности матрица объекта равна A1 = A + D. Задание параметров Для ввода параметров нажмите букву на схеме, чтобы выбрать матрицу (или многочлен), коэффициенты которых нужно задать. - 31 - Процесс управления На графике строится одна или две функции времени: x вектор состояния, u - вектор выхода, z - оценка состояния x, e = x - z ошибка оценки состояния, y - вектор выхода. Для стохастических систем на графике можно строить элементы матриц K и S (см.описание). Время регулирования для устойчивой линейной системы оценивается по корням характеристического уравнения. В случае необходимости процесс можно продолжить (см. меню). Для стохастических систем, независимо от того, какие функции рисуются на графике, идет счет дифференциального уравнения для S(t) и вычисляется матрица K(t). В момент, когда матрица K выходит на стационарный режим, подается звуковой сигнал (и счет S прекращается). Если это событие не происходит на протяжение одного экрана, то счет нужно продолжить. Ход работы: Задаем параметры:  Переходные процессы:  3. Основные результаты:  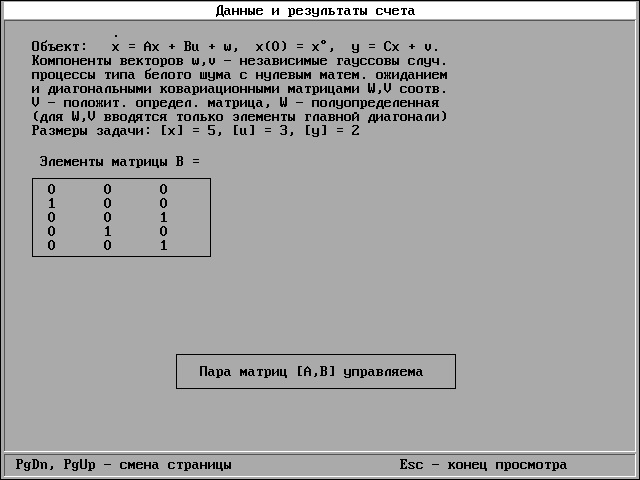   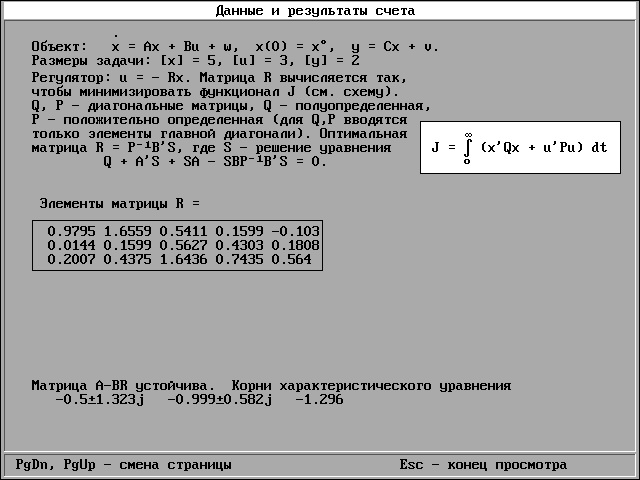   Вывод: По основным результат видим, что система устойчива. Литература:1. Теория автоматического управления. Часть 1. Теория линейных систем автоматического управления. Под ред. А.А. Воронова, М., “Высшая школа”, 1986. 2. Теория автоматического управления. Часть2. Теория нелинейных и специальных систем автоматического управления. Под ред. А.А. Воронова, М., “Высшая школа”, 1986. 3. В.А. Бесекерский, Е.П. Попов. Теория систем автоматического регулирования. М., “Наука”, 1975. 4. Е.П. Попов. Теория линейных систем автоматического регулирования и управления. М., “Наука”, 1989. 5. Е.П. Попов. Теория нелинейных систем автоматического регулирования и управления. М., “Наука”, 1988. 6. А.А. Ерофеев. Теория автоматического управления. С.-П., "Политехника", 1998. |
