Факультет мониторинга окружающей среды
Кафедра физики и высшей математики
Лабораторная работа № 3.02
Измерение сопротивлений мостовым методом
Минск
2014
Лабораторная работа 3.02
Измерение сопротивлений мостовым методом
1. Цель работы. Измерение сопротивления резистора мостовым методом, и проверка законов последовательного и параллельного соединения резисторов.
2. Приборы и принадлежности
Источник постоянного тока, реохорд, магазин сопротивлений, гальванометр, ключ, резисторы с неизвестными сопротивлениями, соединительные провода.
3. Вопросы для допуска к лабораторной работе
Что такое сопротивление проводника? Назовите единицы сопротивления в СИ.
От чего зависит электрическое сопротивление проводника?
Что такое удельное сопротивление проводника? Назовите единицы удельного сопротивления в СИ.
Каким образом могут соединяться проводники в электрических цепях?
Как определить общее сопротивление цепи при последовательном соединении проводников?
Как определить общее сопротивление цепи при параллельном соединении проводников?
Какими преимуществами отличается мостовой метод измерений сопротивлений от иных методов?
Запишите условие сбалансированности мостовой схемы используемой для измерения сопротивления резистора в данной работе.
Чем обусловлено использование в работе гальванометра с нулем на середине шкалы?
Оказывает ли воздействие чувствительность гальванометра на точность измерений сопротивления?
Теоретическое введение
Электрическим током называют направленное движение любых свободных носителей электрических зарядов. Различают: ток проводимости, создаваемый микроскопическими заряженными частицами (электроны, ионы и др.), движущимися внутри неподвижного макроскопического проводника (твердого, жидкого, газообразного); конвекционный ток, который создается зарядами, макроскопических частиц (тел) при движении этих частиц; ток в вакууме, когда свободные заряженные частицы (ионы или электроны) движутся независимо от макроскопических тел.
Электропроводность вещества зависит от природы носителей свободных электрических зарядов (их обычно называют носителями тока). Прохождение тока в металлах и полупроводниках не вызывает каких-либо изменений их химического состава. Из этого следует, что электропроводность металлов и полупроводников обусловлена движением свободных электронов. Вещества, обладающие электронной проводимостью, называются проводниками первого рода.
Растворы и расплавы, проводящие электрический ток, называются электролитами. Носителями тока в электролитах являются свободные ионы, возникающие в результате электролитической диссоциации молекул. Электролиты относятся к проводникам второго рода. Прохождение тока через растворы электролитов всегда сопровождается химическими превращениями и переносом вещества.
Ионизированные газы относятся к проводникам третьего рода. Носителями тока в них являются свободные электроны и ионы, которые возникают под действием внешнего ионизатора или электрического поля, существующего в газе.
Количественными характеристиками тока являются его сила и плотность.
Силой тока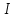 называют физическую скалярную величину, характеризующую интенсивность направленного движения носителей тока и равную отношению заряда, проходящего через поперечное сечение проводника, к промежутку времени. называют физическую скалярную величину, характеризующую интенсивность направленного движения носителей тока и равную отношению заряда, проходящего через поперечное сечение проводника, к промежутку времени.
Если сила тока и его направление не изменяются с течением времени, то ток называют постоянным. В этом случае 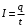 , где , где 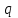 — заряд, проходящий через поперечное сечение проводника за время — заряд, проходящий через поперечное сечение проводника за время 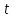 . .
Мгновенное значение силы тока определяется по формуле
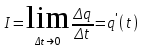 . .
Так как сила тока скалярная величина, то, говоря о его направлении, имеют в виду направление движения положительных зарядов. Поэтому в металлическом проводнике с током электроны упорядоченно движутся в направлении противоположном направлению тока.
Если средняя скорость упорядоченного движения электронов в металлическом проводнике 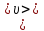 , а их концентрация , а их концентрация 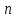 , то за время , то за время 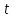 через поперечное сечение проводника проходит заряд через поперечное сечение проводника проходит заряд 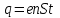 . Принимая во внимание, что . Принимая во внимание, что 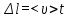 , получаем , получаем 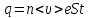 , где , где 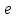 — элементарный заряд; — элементарный заряд; 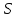 — площадь поперечного сечения проводника. Поэтому сила тока — площадь поперечного сечения проводника. Поэтому сила тока 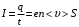 . .
За единицу силы тока в СИ принят — ампер. 1А равен силе неизменяющегося тока, который, проходя по двум параллельным прямолинейным бесконечно длинным проводникам ничтожно малого кругового сечения, находящимся в вакууме на расстоянии d=1 м друг от друга, вызывает между ними силу взаимодействия, модуль которой F= 2·10-7 Н на каждый метр длины.
Плотность тока — физическая векторная величина, равная отношению силы тока 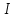 в проводнике к площади поперечного сечения в проводнике к площади поперечного сечения 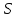 , т. е. , т. е. 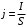 . Если учесть, что . Если учесть, что 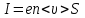 , то , то 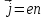 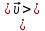 . Направление вектора плотности тока . Направление вектора плотности тока 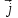 совпадает с направлением вектора скорости совпадает с направлением вектора скорости 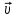 упорядоченного движения положительно заряженных носителей тока. За единицу плотности тока в СИ принят ампер на квадратный метр 1 упорядоченного движения положительно заряженных носителей тока. За единицу плотности тока в СИ принят ампер на квадратный метр 1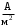 — это плотность электрического тока, при которой сила тока, равномерно распределенного по поперечному сечению проводника площадью 1 м2, составляет 1 А. — это плотность электрического тока, при которой сила тока, равномерно распределенного по поперечному сечению проводника площадью 1 м2, составляет 1 А.
Отметим, что в металлах средняя скорость упорядоченного движения электронов при максимально допустимых значениях силы тока 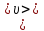 10-4 10-4 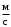 , в то время как средняя скорость их теплового движения , в то время как средняя скорость их теплового движения 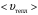 106 106 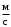 . .
Если ток является постоянным, то распределение зарядов в разных точках проводника с течением времени не изменяется, хотя заряды при этом непрерывно движутся. Электрическое поле таких зарядов называется стационарным. Главная роль в создании стационарного электрического поля в проводнике принадлежит зарядам, находящимся на полюсах источника тока. При замыкании электрической цепи взаимодействие этих зарядов со свободными зарядами проводника ведет к возникновению на всей поверхности проводника нескомпенсированных поверхностных зарядов, причем плотность их постепенно уменьшается по мере удаления от положительного полюса источника тока. Именно эти заряды создают стационарное электрическое поле внутри проводника по всей его длине.
Процесс, Как свидетельствуют опыты, электрическое поле в проводнике становится стационарным через промежуток времени 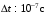 после замыкания цепи. Это обусловлено электромагнитным характером взаимодействия зарядов, скорость которого, немного меньше скорости света в вакууме ( после замыкания цепи. Это обусловлено электромагнитным характером взаимодействия зарядов, скорость которого, немного меньше скорости света в вакууме (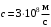 ) . ) .
В состав проводника, кроме свободных зарядов, входят незаряженные частицы и связанные заряды. Все они участвуют в хаотическом тепловом движении, равновероятном во всех направлениях. При наложении электрического поля под действием электрических сил возникает преобладающее направление упорядоченного движения свободных зарядов. Под воздействием электрического поля свободная заряженная частица вещества должна двигаться ускоренно. В проводниках свободные заряды двигаются с некоторой постоянной средней скоростью. Следовательно, проводник оказывает сопротивление упорядоченному движению свободных зарядов, часть энергии этого движения передается проводнику и превращается в его внутреннюю энергию.
Физическая скалярная величина, характеризующая свойство проводника уменьшать скорость упорядоченного движения свободных зарядов, называется электрическим сопротивлением 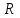 проводника (активным сопротивлением). проводника (активным сопротивлением).
В СИ единицей сопротивления проводника является ом (Ом). 1 Ом – сопротивление такого проводника, сила тока в котором I=1А при напряжении U=1 В между концами этого проводника.
Физическую величину 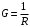 , называют электрической проводимостью. Единицей электрической проводимости в СИ является сименс: 1 См–это проводимость проводника сопротивлением 1 Ом. , называют электрической проводимостью. Единицей электрической проводимости в СИ является сименс: 1 См–это проводимость проводника сопротивлением 1 Ом.
В простейшей модели металлического проводника рассматривать его сопротивление как результат столкновений упорядоченно движущихся, свободных электронов, с ионами кристаллической решетки, то оно должно быть прямо пропорционально длине проводника 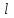 , потому что на большей длине будет больше столкновений. Благодаря движению свободных зарядов искажается даже идеальная кристаллическая решетка проводника и именно на искажениях кристаллической структуры рассеивается энергия упорядоченного движения свободных зарядов. Количество искажений на единицу поперечного сечения и их величина уменьшаются при увеличении площади поперечного сечения , потому что на большей длине будет больше столкновений. Благодаря движению свободных зарядов искажается даже идеальная кристаллическая решетка проводника и именно на искажениях кристаллической структуры рассеивается энергия упорядоченного движения свободных зарядов. Количество искажений на единицу поперечного сечения и их величина уменьшаются при увеличении площади поперечного сечения 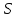 проводника, поэтому сопротивление проводника должно быть обратно пропорционально этой площади. Из сказанного выше следует, что проводника, поэтому сопротивление проводника должно быть обратно пропорционально этой площади. Из сказанного выше следует, что 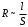 . Для экспериментальной проверки этой зависимости можно воспользоваться той же электрической схемой, что и для проверки закона Ома, включая в участок цепи различные по размерам проводники цилиндрической формы, изготовленные из одного и того же материала, а также из разных материалов. . Для экспериментальной проверки этой зависимости можно воспользоваться той же электрической схемой, что и для проверки закона Ома, включая в участок цепи различные по размерам проводники цилиндрической формы, изготовленные из одного и того же материала, а также из разных материалов.
Введем коэффициент пропорциональности и запишем последнюю зависимость в виде равенства R=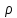 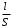 , где , где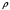 — удельное сопротивление вещества проводника. — удельное сопротивление вещества проводника.
Таким образом, сопротивление однородного металлического проводника постоянного сечения зависит от его геометрических размеров, формы и вещества, из которого изготовлен проводник.
Удельное сопротивление 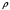 проводника – скалярная физическая величина, численно равная сопротивлению однородного цилиндрического проводника, изготовленного из данного вещества и имеющего длину l=1 м и площадь поперечного сечения S=1 м2 (сопротивлению куба с ребром l =1 м). Единицей удельного сопротивления в СИ является ом·метр (Ом·м). проводника – скалярная физическая величина, численно равная сопротивлению однородного цилиндрического проводника, изготовленного из данного вещества и имеющего длину l=1 м и площадь поперечного сечения S=1 м2 (сопротивлению куба с ребром l =1 м). Единицей удельного сопротивления в СИ является ом·метр (Ом·м).
Удельное сопротивление металлического проводника зависит от следующих факторов:
1) концентрации свободных электронов в проводнике;
2) интенсивности рассеивания свободных электронов на ионах кристаллической решетки, совершающих тепловые колебания;
3) интенсивности рассеивания свободных электронов на дефектах и примесях кристаллической структуры.
Наименьшим удельным сопротивлением обладают серебро и медь. Очень велико удельное сопротивление у сплава никеля, железа, хрома и марганца – "нихрома". Удельное сопротивление металлов в значительной степени зависит от наличия в них примесей. Например, введение 1 % примеси марганца увеличивает удельное сопротивление меди в три раза.
Согласно экспериментально установленному закону Ома: сила тока в однородном металлическом проводнике прямо пропорциональна напряжению между его концами и обратно пропорциональна сопротивлению этого проводника, т. е.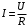 . Если учесть, что . Если учесть, что 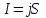 , где , где 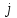 — плотность тока; — плотность тока; 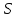 — площадь поперечного сечения проводника, и кроме того, — площадь поперечного сечения проводника, и кроме того, 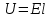 , где , где 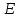 — напряженность электрического поля в проводнике; — напряженность электрического поля в проводнике; 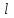 — его длина, и, наконец, — его длина, и, наконец, 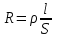 , где , где 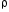 — удельное сопротивление проводника, то закон Ома можно записать в виде — удельное сопротивление проводника, то закон Ома можно записать в виде 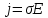 , где , где 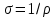 — удельная проводимость проводника. — удельная проводимость проводника.
Все электрические приборы от нагревателей и электрических ламп до стереофонических усилителей оказывают сопротивление проходящему через них току. Соединительные провода обладают, как правило, очень низким сопротивлением. Во многих схемах, в частности в электронных приборах, для управления силой тока используют резисторы, которые могут иметь электрическое сопротивление от долей ома до 106 Ом (МОм). На рисунке 1 показаны некоторые типы резисторов. Обычно резисторы бывают двух основных типов: проволочные (представляющие собой катушки тонкой проволоки) и непроволочные (обычно изготовленные на основе углеродной пленки).
Сопротивление резистора указывается на корпусе цифрами или цветовым кодом.
Цветовой код (маркировка) наносится в виде четырёх или пяти цветных колец. Каждому цвету соответствует определённое цифровое значение (табл. 2). У резисторов с четырьмя цветными кольцами первое и второе кольца обозначают значение сопротивления в омах, третье кольцо - множитель, на который необходимо умножить номинальную величину сопротивления, а четвертое кольцо определяет величину допуска в процентах.
Для резисторов с точностью 20 % используют маркировку с тремя кольцами, для резисторов с точностью 10 % и 5 % маркировку с четырьмя кольцами, для более точных резисторов с пятью или шестью кольцами. Первые два кольца всегда означают первые два знака номинала. Если колец 3 или 4, третье кольцо означает десятичный множитель, то есть степень десятки, которая умножается на двузначное число, указанное первыми двумя кольцами. Если колец 4, последнее указывает точность резистора. Если колец 5, третье означает третий знак сопротивления, четвёртое — десятичный множитель, пятое — точность. Шестое кольцо, если оно есть, указывает температурный коэффициент сопротивления (ТКС). Следует отметить, что иногда встречаются резисторы с 5-ю кольцами, но стандартной (5 или 10 %) точностью. В этом случае первые два кольца задают первые знаки номинала, третье — множитель, четвёртое — точность, а пятое — температурный коэффициент сопротивления.
Поскольку резистор симметричная деталь, может возникнуть вопрос: «Начиная, с какой стороны читать полоски?» Для четырёх полосной маркировки обычных резисторов с точностью 5 и 10 % вопрос решается просто: золотая или серебряная полоска всегда стоит в конце. Для трёхполосного кода первая полоска стоит ближе к краю резистора, чем последняя. Для других вариантов важно, чтобы получалось значение сопротивления из номинального ряда, если не получается, нужно читать наоборот.
Маркировка отечественных резисторов.
Таблица 2
Цвет знака
|
Номинальное сопротивление, Ом
|
Допуск,
%
|
Первая
цифра
|
Вторая
цифра
|
Третья
цифра
|
Множитель
|
Серебристый
|
|
10-2
|
±10
|
Золотистый
|
10-1
|
±5
|
Черный
|
|
0
|
0
|
1
|
|
Коричневый
|
1
|
1
|
1
|
10
|
±1
|
Красный
|
2
|
2
|
2
|
102
|
±2
|
Оранжевый
|
3
|
3
|
3
|
103
|
|
Желтый
|
4
|
4
|
4
|
104
|
Зеленый
|
5
|
5
|
5
|
105
|
0,5
|
Голубой
|
6
|
6
|
6
|
106
|
±0,25
|
Фиолетовый
|
7
|
7
|
7
|
107
|
±0,1
|
Серый
|
8
|
8
|
8
|
108
|
±0,05
|
Белый
|
9
|
9
|
9
|
109
|
|
 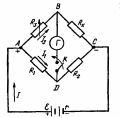
Рис. 2
Для точного измерения сопротивлений используют так называемые мостовые схемы. Самой распространенной из них является схема мостика Уинстона (рис. 2).Четыре резистора R1, R2, R3 и Rх образуют "плечи" схемы. Участок цепи, содержащий гальванометр представляет собой как бы мостик, соединяющий точки В иD. После подключения источника тока к клеммам мостика А и С в цепи проходит ток. Чтобы измерить Rх, переменное сопротивление резистораR3изменяютдо тех пор, пока точкиB и D схемы не будут иметь одинаковые потенциалы
φА= φD (при этом стрелка гальванометра не отклоняется при замкнутом ключе К). В таком случае говорят, что мост сбалансирован (уравновешен).
5. Методика измерений и обработка результатов
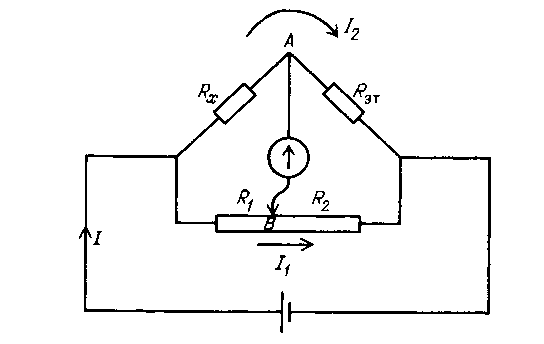 Принципиальная схема электрической цепи для измерения сопротивления мостовым методом приведена на рисунке 3. Принципиальная схема электрической цепи для измерения сопротивления мостовым методом приведена на рисунке 3.

Рис. 3 3унок 3
Условие сбалансированности достигается, когда ток через гальванометр отсутствует. Поскольку для измерения малых токов можно использовать очень чувствительный гальванометр, то условие сбалансированность мостика может быть установлена очень точно. В отсутствие тока через гальванометр цепь состоит просто из двух параллельных ветвей. Создаваемый источником ток делится на нижний ток I1 и верхний ток I2. Напряжение на неизвестном резисторе Rх должно быть таким же, как и напряжение на резисторе R1, аналогично напряжение на эталонном резисторе Rэт должно быть таким же, как и напряжение на R2.
Приравняв эти напряжения и поделив полученные уравнения почленно, получим:
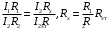
Эта формула позволяет определить сопротивление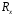 , если сопротивления , если сопротивления 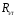 , ,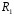 и и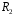 известны. известны.
В данной работе эталонным резистором, является сопротивление Rэт магазина сопротивлений Р–33. Двумя другими сопротивлениями являются сопротивления плеч реохорда – калиброванного проводника, натянутого вдоль миллиметровой шкалы, по которому скользит подвижный контакт. Сопротивления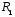 и и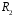 плеч реохорда пропорциональны их длине плеч реохорда пропорциональны их длине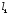 и и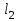 : :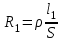 , , 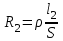 . .
Поэтому 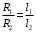 . Откуда . Откуда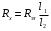 . .
Таким образом, измерение сопротивления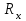 сводится к установке на магазине сопротивления сводится к установке на магазине сопротивления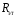 и отысканию на реохорде такого положения подвижного контакта, при котором сила тока в гальванометре будет равна нулю. и отысканию на реохорде такого положения подвижного контакта, при котором сила тока в гальванометре будет равна нулю.
В качестве индикатора тока в работе используется мультиметрDT830B. При перемещении подвижного контакта реохорда показания мультиметра (предел 200 мА) проходят через нуль и при дальнейшем перемещении подвижного контакта, на дисплее высвечивается знак «минус».
ЗАДАНИЕ 1.
Соберите электрическую цепь в соответствии со схемой, приведенной на рисунке 3.
На магазине сопротивлений установите сопротивление 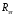 =20 Ом и добейтесь нулевого показания мультиметра. =20 Ом и добейтесь нулевого показания мультиметра.
Повторите измерения для значений 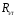 : 40 Ом, 60 Ом, 80 Ом и 100 Ом. : 40 Ом, 60 Ом, 80 Ом и 100 Ом.
Рассчитайте значение R1x.
Результаты измерений и вычислений занесите в таблицу.
№ п/п
|
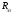 , Ом , Ом
|
l1,мм
|
l2, мм
|
R1х, Ом
|
1x>, Ом
|
20
|
|
|
|
|
|
…
|
|
|
|
|
100
|
|
|
|
|
ЗАДАНИЕ 2.
На магазине сопротивлений установите сопротивление 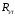 =50 Ом и добейтесь нулевого показания мультиметра. =50 Ом и добейтесь нулевого показания мультиметра.
Повторите измерения для значений 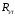 : 50 Ом, 100 Ом, 150 Ом, 200 Ом, 250 Ом. : 50 Ом, 100 Ом, 150 Ом, 200 Ом, 250 Ом.
Рассчитайте значение R2x.
Результаты измерений и вычислений занесите в таблицу.
№ п/п
|
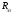 , Ом , Ом
|
l1,мм
|
l2, мм
|
R2x,Ом
|
2x>, Ом
|
50
|
|
|
|
|
|
…
|
|
|
|
|
250
|
|
|
|
|
ЗАДАНИЕ 3.
Соедините резисторы R1x и R2x последовательно.
Сбалансируйте электрическую цепь
Рассчитайте общее сопротивление 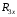 двух резисторов при двух резисторов при 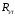 : 40 Ом, : 40 Ом,
80 Ом, 120 Ом, 160 Ом, 200 Ом.
№ п/п
|
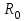 , Ом , Ом
|
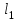 , мм , мм
|
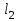 , мм , мм
|
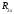 , Ом , Ом
|
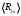 , Ом , Ом
|
|
|
|
|
|
|
|
|
|
|
|
|
ЗАДАНИЕ 4.
Соедините резисторы R1x и R2x параллельно.
Сбалансируйте электрическую цепь
Рассчитайте общее сопротивление 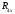 двух резисторов при двух резисторов при 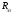 : 40 Ом, : 40 Ом,
80 Ом, 120 Ом, 160 Ом, 200 Ом.
№ п/п
|
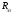 , Ом , Ом
|
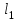 , мм , мм
|
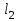 , мм , мм
|
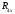 , Ом , Ом
|
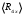 , Ом , Ом
|
|
|
|
|
|
|
|
|
|
|
|
|
По результатам выполнения каждого задания запишите ответы и сформулируйте выводы.
Выключите электрооборудование и приведите рабочее место в порядок.
6. Вопросы для самоконтроля
Дайте определение электрического тока. Что принимают за величину тока, за направление тока?
Дайте определение единицы силы тока в СИ.
Что называют плотностью тока?
В каких единицах измеряют сопротивление и удельное сопротивление проводника?
От чего зависит сопротивление проводника при данной температуре?
Получите формулы для расчета сопротивления участка цепи при
последовательном и параллельном соединениях проводников.
Докажите, что погрешность измерения сопротивления будет минимальной, если длины плеч реохорда одинаковые (l1=l2).
Литература
1. Физика. Учебник/И.Н. Наркевич, Э.И. Волмянский, С.И. Лобко.–Мн: Новое знание, 2004.
2. Физика. Учебное пособие/В.А. Бондарь, А.А. Луцевич, О.А. Новицкий и [др.]; Под общ. ред. В.А. Яковенко.–Мн: БелЭн, 2002.
3. Луцевич А.А. Физика: Весь школьный курс в таблицах/ А.А. Луцевич.– Мн: Юнипресс, 2010.
4. Общая физика. Практикум: Учеб. Пособие/ В.А. Бондарь и [др.]; под общ. ред. В.А. Яковенко.–Мн: Высшая школа, 2008.
5. Физический практикум/А.М. Саржевский, В.П. Бобрович, Г.Н. Борздов и [др.]; под ред. Г. С. Кембровского. Мн.; Университетское, 1986.
6. Савельев И.В. Курс физики: Учеб.: В 3-х т. Т. 2: Электричество. Колебания и волны. Волновая оптика. − М.: Наука. Гл. ред. физ.-мат. лит., 1989.
|
 Скачать 203.06 Kb.
Скачать 203.06 Kb.

 Принципиальная схема электрической цепи для измерения сопротивления мостовым методом приведена на рисунке 3.
Принципиальная схема электрической цепи для измерения сопротивления мостовым методом приведена на рисунке 3.
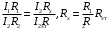
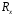 , если сопротивления
, если сопротивления 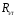 ,
,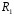 и
и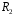 известны.
известны. 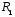 и
и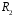 плеч реохорда пропорциональны их длине
плеч реохорда пропорциональны их длине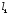 и
и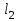 :
: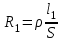 ,
, 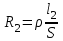 .
. 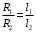 . Откуда
. Откуда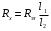 .
.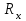 сводится к установке на магазине сопротивления
сводится к установке на магазине сопротивления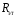 и отысканию на реохорде такого положения подвижного контакта, при котором сила тока в гальванометре будет равна нулю.
и отысканию на реохорде такого положения подвижного контакта, при котором сила тока в гальванометре будет равна нулю. 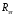 =20 Ом и добейтесь нулевого показания мультиметра.
=20 Ом и добейтесь нулевого показания мультиметра.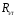 : 40 Ом, 60 Ом, 80 Ом и 100 Ом.
: 40 Ом, 60 Ом, 80 Ом и 100 Ом.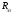 , Ом
, Ом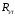 =50 Ом и добейтесь нулевого показания мультиметра.
=50 Ом и добейтесь нулевого показания мультиметра.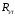 : 50 Ом, 100 Ом, 150 Ом, 200 Ом, 250 Ом.
: 50 Ом, 100 Ом, 150 Ом, 200 Ом, 250 Ом.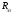 , Ом
, Ом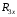 двух резисторов при
двух резисторов при 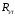 : 40 Ом,
: 40 Ом, 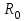 , Ом
, Ом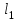 , мм
, мм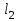 , мм
, мм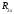 , Ом
, Ом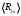 , Ом
, Ом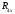 двух резисторов при
двух резисторов при 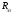 : 40 Ом,
: 40 Ом,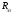 , Ом
, Ом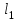 , мм
, мм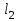 , мм
, мм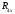 , Ом
, Ом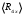 , Ом
, Ом

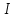
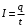 , где
, где 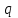 — заряд, проходящий через поперечное сечение проводника за время
— заряд, проходящий через поперечное сечение проводника за время 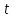 .
.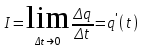 .
.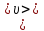 , а их концентрация
, а их концентрация 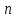 , то за время
, то за время 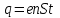 . Принимая во внимание, что
. Принимая во внимание, что 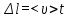 , получаем
, получаем 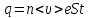 , где
, где 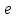 — элементарный заряд;
— элементарный заряд; 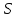 — площадь поперечного сечения проводника. Поэтому сила тока
— площадь поперечного сечения проводника. Поэтому сила тока 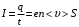 .
.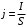 . Если учесть, что
. Если учесть, что 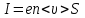 , то
, то 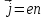
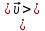 . Направление вектора плотности тока
. Направление вектора плотности тока 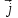 совпадает с направлением вектора скорости
совпадает с направлением вектора скорости 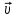 упорядоченного движения положительно заряженных носителей тока. За единицу плотности тока в СИ принят ампер на квадратный метр 1
упорядоченного движения положительно заряженных носителей тока. За единицу плотности тока в СИ принят ампер на квадратный метр 1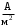 — это
— это 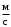 , в то время как средняя скорость их теплового движения
, в то время как средняя скорость их теплового движения 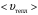 106
106 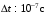 после замыкания цепи. Это обусловлено электромагнитным характером взаимодействия зарядов, скорость которого, немного меньше скорости света в вакууме (
после замыкания цепи. Это обусловлено электромагнитным характером взаимодействия зарядов, скорость которого, немного меньше скорости света в вакууме (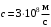 ) .
) .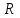 проводника (активным сопротивлением).
проводника (активным сопротивлением).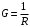 , называют электрической проводимостью. Единицей электрической проводимости в СИ является сименс:
, называют электрической проводимостью. Единицей электрической проводимости в СИ является сименс: 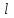 , потому что на большей длине будет больше столкновений. Благодаря движению свободных зарядов искажается даже идеальная кристаллическая решетка проводника и именно на искажениях кристаллической структуры рассеивается энергия упорядоченного движения свободных зарядов. Количество искажений на единицу поперечного сечения и их величина уменьшаются при увеличении площади поперечного сечения
, потому что на большей длине будет больше столкновений. Благодаря движению свободных зарядов искажается даже идеальная кристаллическая решетка проводника и именно на искажениях кристаллической структуры рассеивается энергия упорядоченного движения свободных зарядов. Количество искажений на единицу поперечного сечения и их величина уменьшаются при увеличении площади поперечного сечения 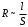 .
. 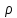
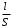
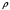 — удельное сопротивление вещества проводника.
— удельное сопротивление вещества проводника.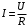 . Если учесть, что
. Если учесть, что 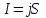 , где
, где 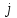 — плотность тока;
— плотность тока; 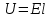 , где
, где 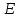 — напряженность электрического поля в проводнике;
— напряженность электрического поля в проводнике; 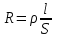 , где
, где 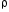 — удельное сопротивление проводника, то закон Ома можно записать в виде
— удельное сопротивление проводника, то закон Ома можно записать в виде 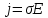 , где
, где 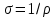 — удельная проводимость проводника.
— удельная проводимость проводника.