5. Кривая намагничивания. Лабораторная работа 06 снятие кривой намагничивания и петли гистерезиса с помощью осциллографа цель работы
 Скачать 1.05 Mb.
|
|
ЛАБОРАТОРНАЯ РАБОТА № 2.06 СНЯТИЕ КРИВОЙ НАМАГНИЧИВАНИЯ И ПЕТЛИ ГИСТЕРЕЗИСА С ПОМОЩЬЮ ОСЦИЛЛОГРАФАЦель работы Целью данной работы является изучение законов электромагнетизма, методов исследования характеристик магнитного поля в веществе, свойств ферромагнетиков и ознакомление со способом опытного изучения магнитных свойств ферромагнетика с помощью осциллографа. Краткая теория Характеристиками магнитного поля являются индукция  и напряженность  . Индукция является силовой характеристикой магнитного поля, численно равной величине силы, с которой магнитное поле действует на единичный элемент тока, помещенный в данную точку поля нормально линиям индукции. В веществе индукция магнитного поля определяется как макроскопическими, так и микроскопическими токами. Напряженность является вспомогательной физической величиной, характеризующей намагничивающее поле.При внесении в магнитное поле все вещества намагничиваются, т. е. магнитное поле в веществе отличается от внешнего магнитного поля. Магнитное поле в веществе можно представить в виде:  , (2.06.1)где – магнитное поле в веществе;  – внешнее магнитное поле,  – внутреннее магнитное поле, возникающее за счет ориентации магнитных моментов структурных элементов вещества.Характеристикой магнитного состояния вещества является намагниченность, численно равная суммарному магнитному моменту единицы объема вещества.  , (2.06.2)где V – физически малый объем вещества;  – магнитный момент i-го атома. Суммирование осуществляется по всем атомам, находящимся в физически малом объеме V. Опыт показывает, что для большинства веществ намагниченность пропорциональна напряженности намагничивающего поля.  , (2.06.3)где  – магнитная восприимчивость вещества. В веществе  . (2.06.4)Учитывая (2.06.3), получаем:   (2.06.5)где  – относительная магнитная проницаемость вещества, показывающая, во сколько раз индукция магнитного поля в веществе отличается от магнитной индукции в вакууме. По своим магнитным свойствам и по характеру магнитных структур все вещества делятся на две основные группы: вещества, намагничивающиеся в направлении, противоположном направлению внешнего магнитного поля, и вещества, намагничивающиеся в направлении внешнего магнитного поля. Диамагнетики – вещества, намагничивающиеся в направлении, противоположном направлению намагничивающего поля. Для диамагнетиков  следовательно  . Диамагнитными свойствами обладают вещества, собственные магнитные моменты структурных элементов которых равны нулю в отсутствие внешнего поля. Во внешнем магнитном поле в атомах индуцируются магнитные моменты, ориентированные противоположно намагничивающему полю.Структурные элементы веществ, намагничивающихся в направлении внешнего магнитного поля, обладают собственными магнитными моментами. Эти вещества, в свою очередь, можно разбить на две группы: вещества, не обладающие самопроизвольной ориентацией магнитных моментов структурных элементов, и вещества, у которых магнитные моменты структурных элементов упорядочены в отсутствие внешнего магнитного поля. К первым относятся парамагнетики. У парамагнетиков  и соответственно  . Магнитные моменты атомов парамагнетиков в отсутствие внешнего магнитного поля разупорядочены вследствие теплового движения. Во внешнем магнитном поле возникает преимущественная ориентация магнитных моментов атомов парамагнетика. Магнитная восприимчивость парамагнетиков невелика и не зависит от величины напряженности намагничивающего поля. Некоторые парамагнетики при достаточно низких температурах могут переходить в ферромагнитное или антиферромагнитное состояние.Ко второй группе относятся ферромагнетики, антиферромагнетики и ферримагнетики (ферриты). Н 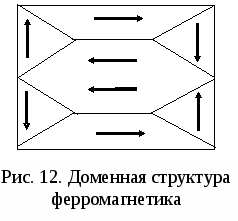 аибольший практический интерес представляют ферромагнетики – вещества, обладающие намагниченностью в отсутствие внешнего магнитного поля. Магнитная проницаемость ферромагнетиков имеет большую величину  и зависит от напряженности внешнего магнитного поля и предшествующего магнитного состояния вещества. Для каждого ферромагнетика существует характерная температура, выше которой вещество теряет ферромагнитные свойства и становится парамагнетиком. Эта температура называется точкой Кюри  . Ферромагнитными свойствами обладают железо, кобальт, никель, их сплавы, некоторые редкоземельные элементы, а также некоторые химические соединения. Особые свойства ферромагнетиков связаны с наличием в них малых самопроизвольно намагниченных областей – магнитных доменов. Размеры доменов составляют несколько микрометров. В пределах одного домена магнитные моменты атомов ориентированы в одном направлении. В ненамагниченном состоянии домены ориентированы хаотически и результирующая намагниченность равна нулю. Однако они имеют стремление располагаться так, чтобы образовались замкнутые магнитные цепи, так что магнитная энергия имеет наименьшую величину. Это схематически изображено на рис. 12, где стрелками показано направление магнитных моментов отдельных доменов. Е 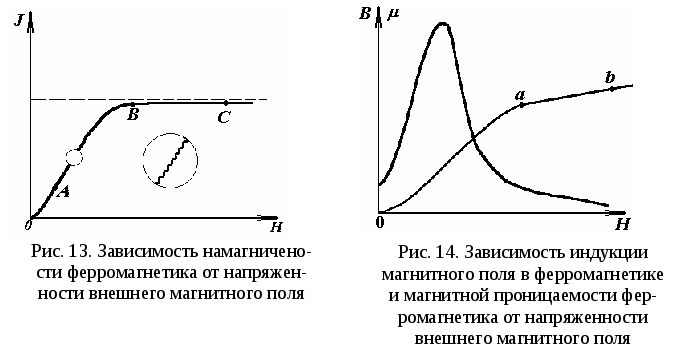 сли поместить ферромагнетик во внешнее магнитное поле, он намагничивается. При малых значениях напряженности внешнего поля происходит увеличение размеров тех доменов, ориентация магнитного момента которых близка к направлению внешнего магнитного поля. Этот процесс соответствует участку ОА зависимости намагниченности ферромагнетика от напряженности внешнего магнитного поля (рис. 13). Если поле увеличивать (участок АВ на рис. 13), то процесс смещения границ доменов сменяется процессом вращения. Магнитные моменты целых доменов начинают поворачиваться одновременно. Данный процесс протекает не плавно, а ступенчато, что видно из кривой намагничивания  , е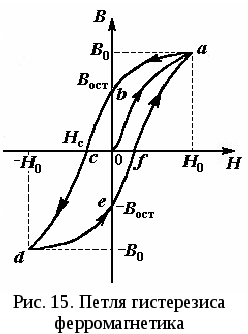сли ее строить в увеличенном масштабе (см. рис. 13). При дальнейшем увеличении намагничивающего поля происходит магнитное насыщение. При этом магнитные моменты всех доменов ориентированы по полю (участок ВС на рис. 13). Намагниченность незначительно увеличивается при увеличении поля за счет тех магнитных моментов, которые разориентированы тепловым движением. В процессе намагничивания магнитная проницаемость сначала растет, затем уменьшается и при насыщении становится близка к единице. Зависимость индукции магнитного поля (кривая намагничивания) и магнитной проницаемости ферромагнетика от напряженности внешнего магнитного поля показаны на рис. 13 и 14. Е  сли ферромагнетик сначала намагнитить полем напряженности H0 до индукции В0, а затем уменьшать намагничивающее поле Н до нуля, то индукция будет уменьшаться с некоторым отставанием (рис. 15). Когда напряженность станет равной нулю, индукция будет равна некоторому значению Вост, характеризующему остаточное намагничивание. Наличие остаточного намагничения объясняется тем фактом, что некоторые домены остаются ориентированными по полю и обеспечивают намагниченность ферромагнетика при нулевом намагничивающем поле. Явление отставания изменения индукции магнитного поля В в ферромагнетике от изменения напряженности Н в процессе перемагничивания называется гистерезисом. Если увеличивать напряженность поля Н в обратном направлении от нуля до некоторого значения НС, называемого коэрцитивной силой, индукция поля уменьшается до нуля. При дальнейшем увеличении напряженности до (–H0) ферромагнетик перемагничивается до индукции (–B0). При изменении напряженности поля от ( –H0) до нуля, вновь возникает остаточное намагничивание. Изменяя напряженность поля в первоначальном направлении до значения Н0, снова получим значение индукции В0. Таким образом, при изменении напряженности от (+H0) до (–H0) и обратно, ферромагнетик пройдет полный цикл перемагничивания, кривая зависимости В = f(H) будет иметь вид замкнутой петли, называемой петля гистерезиса (см. рис. 15). Площадь петли гистерезиса пропорциональна энергии, расходуемой на перемагничивание. Чтобы размагнитить ферромагнетик его можно поместить в переменное магнитное поле и провести несколько циклов перемагничивания, постепенно уменьшая амплитудные значения напряженности поля. Петлю гистерезиса можно получить на экране электронно-лучевой трубки осциллографа. Исследуемым ферромагнитным веществом является трансформаторная сталь, из которой изготовлен прямоугольный сердечник трансформатора. На сердечник намотаны две катушки: первичная – намагничивающая с числом витков N1 и вторичная - измерительная с числом витков N2. Первичная катушка N1 через эталонный резистор R8 и потенциометр R1 подключена к генератору переменного тока Г. Для измерения амплитудного значения силы тока I1 в первичной цепи используется электронный осциллограф ЭО, вход X которого подключается к эталонному резистору R8. Принципиальная схема опыта по исследованию кривой намагничивания и петли гистерезиса ферромагнетика показана на рис. 16. Т 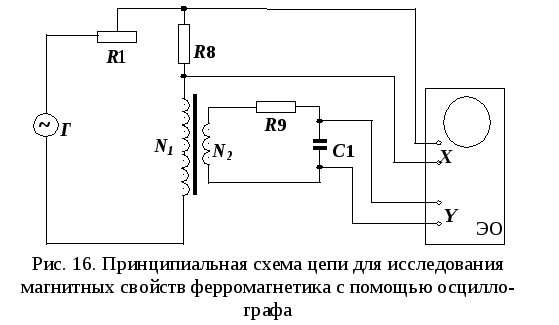 ок I1 создает в сердечнике намагничивающее поле напряженностью Н. Напряженность магнитного поля в длинной катушке, согласно теореме о циркуляции:  (2.06.6)где l– длина ферромагнитного сердечника. Формула (2.06.6) справедлива для мгновенных значений напряженности поля и тока, а также, в частности, для амплитудных значений. Напряжение на резисторе R8 пропорционально силе тока I1, а значит, и напряженности Н магнитного поля.  (2.06.7)Таким образом, на вход Xподается напряжение, пропорциональное напряженности магнитного поля H. В соответствии с законом Фарадея ЭДС индукции в катушке  (2.06.8)где – магнитный поток, сцепленный с каждым витком катушек N1 и N2. По определению  (2.06.9)где S – площадь одного витка. Тогда  (2.06.10)Так как ЭДС индукции пропорциональна скорости изменения магнитной индукции, то для определения величины В во вторичную цепь включено интегрирующее устройство. Функцию последнего выполняет интегрирующая цепочка, состоящая из резистора R9 и конденсатора C1. Можно показать, что напряжение на конденсаторе пропорционально интегралу от силы тока во вторичной катушке I2. 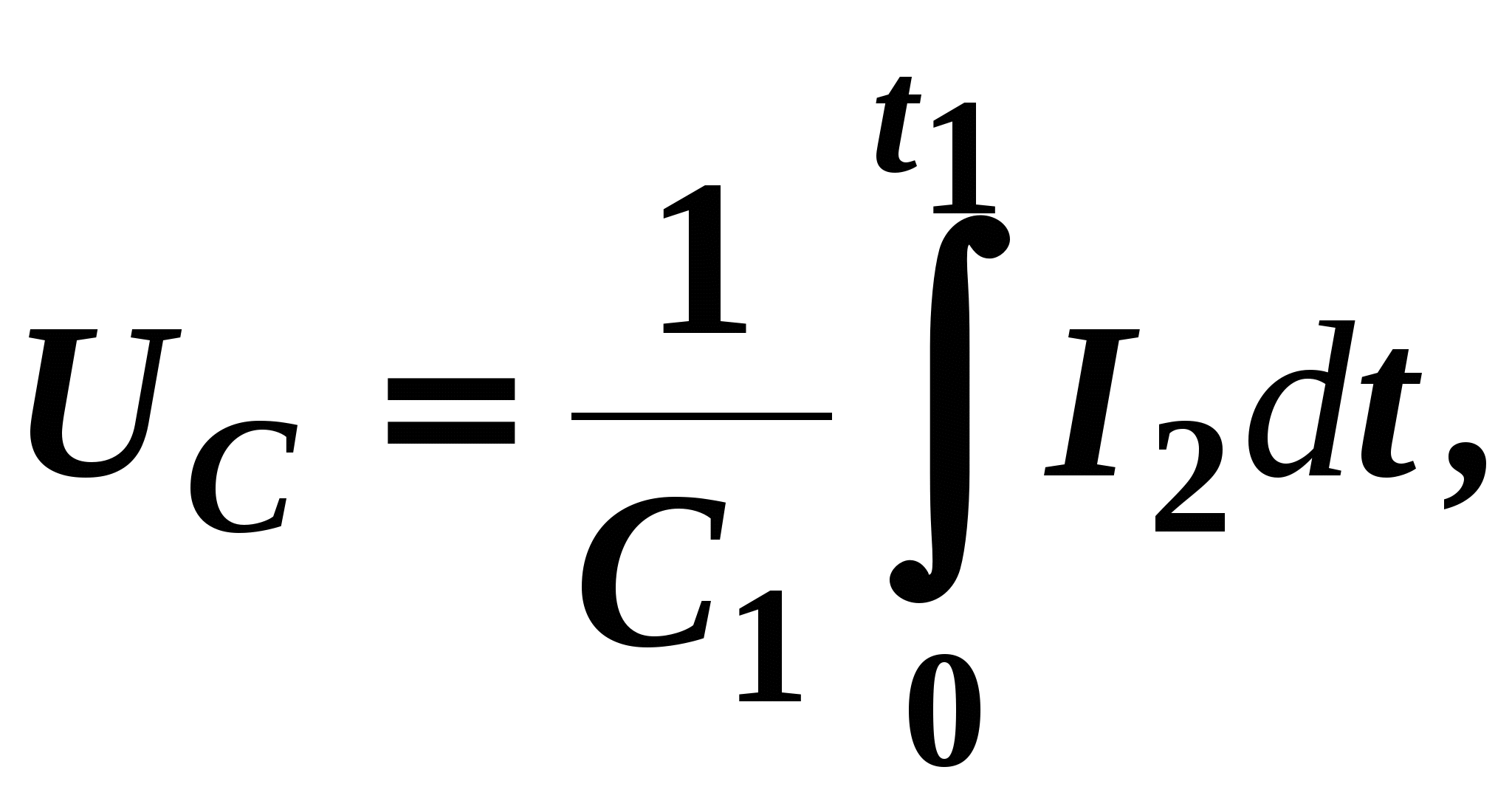 (2.06.11)где t1 – время интегрирования, соизмеримое с периодом колебания тока промышленной сети. Для интегрирущего звена омическое сопротивление обычно выбирается значительно бόльшим емкостного сопротивления 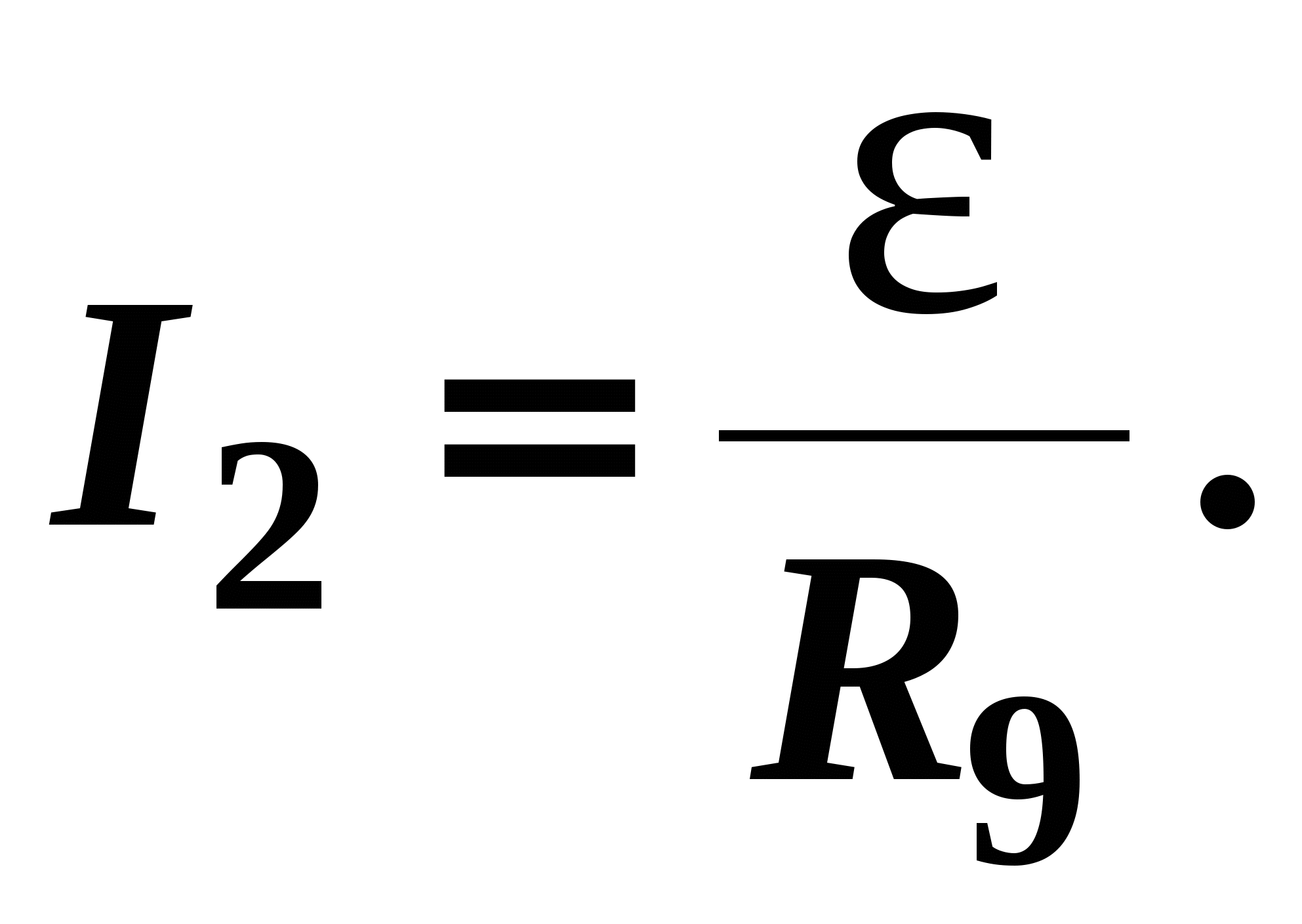 ( – круговая частота). В этом случае сила тока I2 практически полностью определяется величиной R9 и по закону Ома (2.06.12)Из (2.06.11) с учетом (2.06.12) и (2.06.10) получаем, что напряжение на конденсаторе 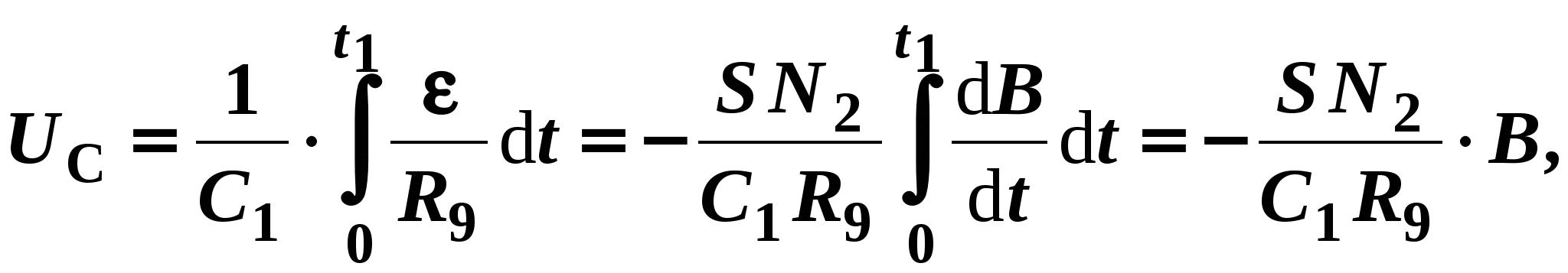 (2.06.13)и, следовательно, магнитная индукция  (2.06.14)Т. о., напряжение, снимаемое с конденсатора и подаваемое на вертикально отклоняющие пластины ЭЛТ (вход Y), пропорционально индукции магнитного поля в сердечнике. Формула (2.06.14) справедлива, в частности, для амплитудных значений напряжения на конденсаторе UС и индукции В. Если увеличивать силу тока в первичной катушке, площадь петли гистерезиса будет сначала увеличиваться. Таким образом будут наблюдаться частные петли гистерезиса. При некотором значении силы тока дальнейшего увеличения площади петли происходить не будет. Наибольшая по площади петля гистерезиса будет являться предельной. По известным значениям В и Н можно вычислить магнитную проницаемость трансформаторной стали  (2.06.15)В эксперименте предлагается оценить также мощность, затраченную на перемагничивание материала. При перемагничивании образца энергия расходуется на переориентацию доменов и выделяется в виде тепла. Величина этой энергии W, приходящейся на единицу объема образца, численно равна площади S1 петли гистерезиса. Если частота переменного тока 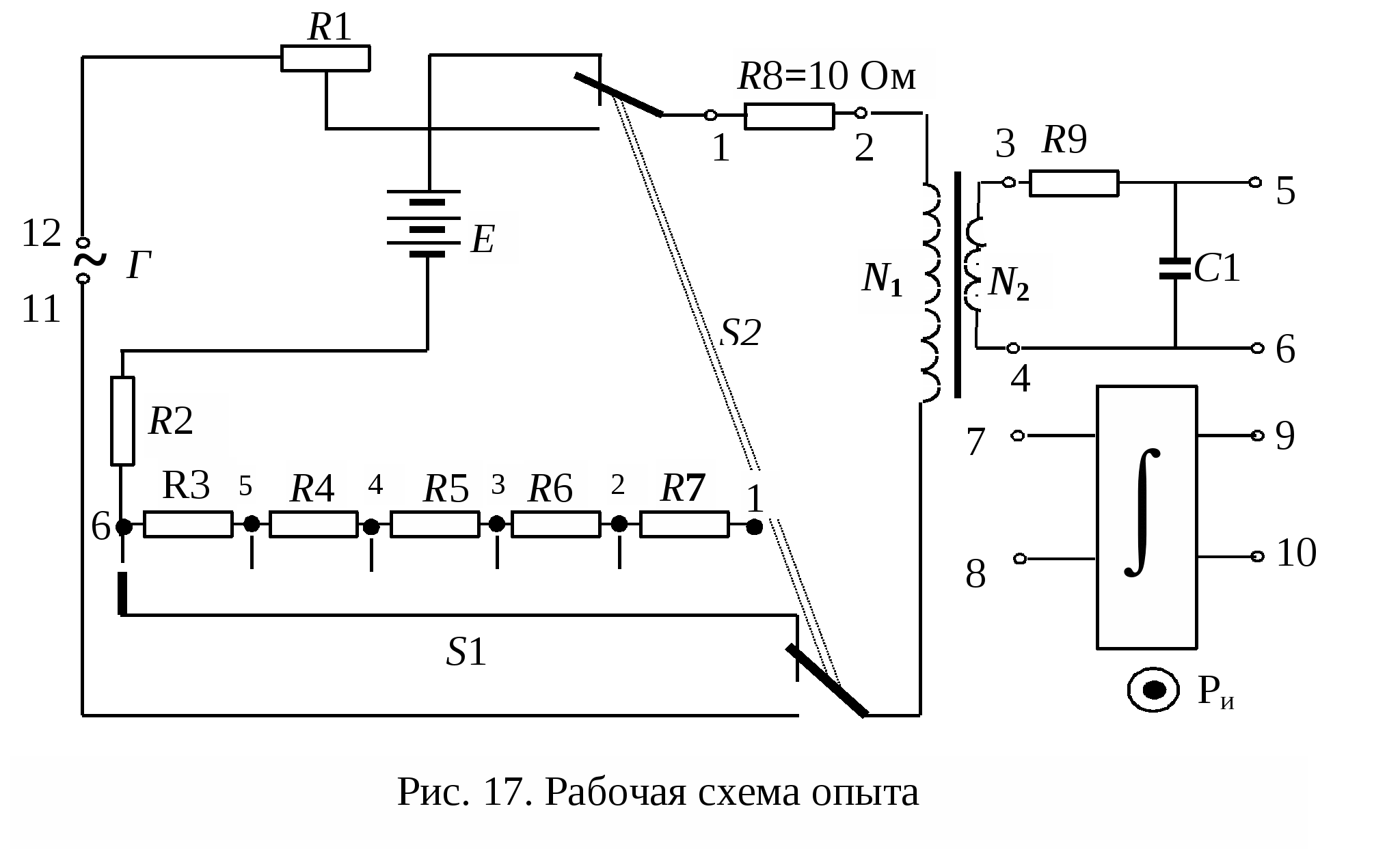 , то количество тепла, выделяемое за единицу времени, будет равно мощности, затрачиваемой на перемагничивание единицы объема. (2.06.16)П  лощадь петли гистерезиса определяем по числу клеток, занимаемых ею на экране осциллографа. Если цена деления по оси Н равна ZH, а по оси В равна ZB, тогда величина площади петли будет равна  , где N– площадь петли в малых делениях шкалы осциллографа. Потери на перемагничивание, следовательно, будут равны: (2.06.17)В данной работе частота переменного тока равна частоте в промышленных сетях  .Выполнение работы Необходимые приборы и материалы: ферромагнитный сердечник с катушками N1 и N2 (N1 = 2000, N2= 1000 витков, l= 0,1 м, S= 1·10-4 м2); резистор R8; генератор переменного тока Г; электронный осциллограф ЭО; интегрирующая цепь R9, C1 (R9 = 160 кОм, C1 = 3,9 мкФ). Все элементы схемы, кроме осциллографа, смонтированы внутри лабораторного стенда. Рабочая схема опыта для исследования кривой намагничивания и петли гистерезиса ферромагнетика показана на рис. 17 и на панели стенда. Порядок выполнения работы
Вращая ручку потенциометра R1, можно изменять силу тока в первичной цепи. Для каждого значения тока на экране осциллографа возникает петля гистерезиса соответствующего размера. Начиная с некоторого значения силы тока, площадь петли практически перестает возрастать, т. е. наблюдается предельная петля гистерезиса. Перед началом измерений убедитесь в этом, просматривая на экране осциллографа петли гистерезиса при различных значениях силы тока I1.
Для определения напряженности (H) и индукции (B) магнитного поля по формулам (2.06.6) и (2.06.14) необходимо измерить силу тока в первичной цепи I1 и напряжение на конденсаторе Uc. Начинать измерения удобно с предельной петли гистерезиса.
а) опустить перпендикуляр из вершины петли на ось OX; б) полученное число маленьких делений умножить на цену одного деления I канала, получив, тем самым НАПРЯЖЕНИЕ НА РЕЗИСТОРЕ R8; в) полученное значение напряжения на резисторе R8 в соответствии с законом Ома делим на величину сопротивления (R8 = 10 Ом): I1=UR8/R8=UR8/10. Результат записываем в табл. 6.1.
Таблица 6.1 Результаты измерений
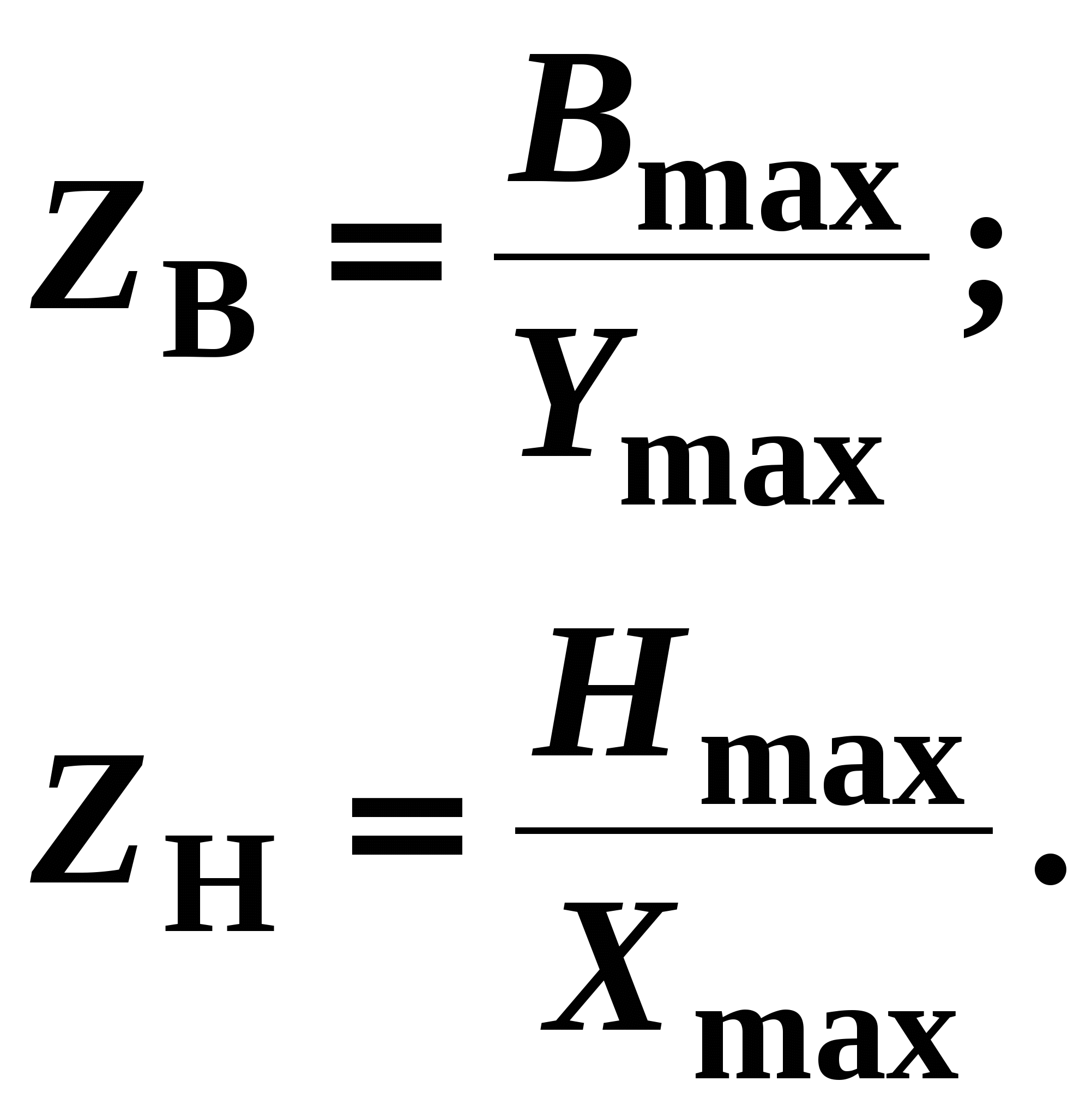 Вычислите потери на перемагничивание по формуле (2.06.17) в Вт/м–3. По результатам лабораторной работы сделайте выводы о характере установленных зависимостей индукции магнитного поля и магнитной проницаемости от напряженности магнитного поля для исследованного ферромагнетика. КОНТРОЛЬНЫЕ ВОПРОСЫ
РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА Калашников С. Г. Электричество. М.: Наука, 1970. 257 – 266 с. Савельев И. В. Курс общей физики. Т. 2. М.: Наука, 1982. 176 – 180 с. Трофимова Т. И. Курс общей физики: М.: Высшая школа, 1985. 203 – 213 с. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
и “” выведите изображение точки в центр экрана. Поверните ручку потенциометра R1 до упора вправо. Ручками регулировки коэффициентов усиления первого и второго каналов добейтесь, чтобы величина максимальной петли была в пределах экрана.