Лабораторная работа 1, Коневец Арсений Б9120-09.03.03пикд. Лабораторная работа 1 1 Сколько различных четырехзначных целых чисел можно составить из цифр 1, 3, 3, 7, 7, 8
 Скачать 69.9 Kb. Скачать 69.9 Kb.
|
|
Коневец Арсений Лабораторная работа №1 1) Сколько различных четырехзначных целых чисел можно составить из цифр 1, 3, 3, 7, 7, 8? Сначала найдем количество выборок, в которых все цифры разные: P4 = 4! = 24, затем найдем количество выборок, в которых две тройки, но только одна семерка, будет 6 вариантов расположения троек, и для каждого 3 * 2 = 6 выборок: 6 * 6 = 36, аналогично для выборок, в которых две семерки и одна тройка. Выборок, в которых две семерки и две тройки, 6. Таким образом, всего выборок будет: 24 + 36 * 2 + 6 = 102 числа. 2) а) Сколькими способами 8 человек (A, B, ..., H) могут занять места за квадратным столом с точностью до ротации ((a), (b) - одинаковые, (a), (c) - разные)? По формуле перестановки получаем 8!, однако нам не нужны ротации этих перестановок, коих для каждой выборки 8, следовательно, делим получившееся на 8: 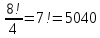 б) Два человека (A, B) не должны сидят рядом. Сначала найдем, сколько выборок, в которых два человека сидят рядом – 2 * 6! * 4 = 5760, количество выборок, в которых они не сидят рядом: 8! – 10080 = 34560. в) Два человека (A, B) не должны сидят напротив друг друга. Количество выборок, в которых два человека сидят напротив: 2 * 6! * 4 = 5760, количество выборок, в которых они не сидят напротив: 8! – 5760 = 34560. 3) 3 города связаны сетью двусторонних дорог: а) Сколько различных способов добраться из A в C? По правилам суммы и умножения имеем: 3 * 4 + 2 = 14 способов. б) Сколько различных способов совершить путешествие из A в C и обратно? Из А в С можно добраться 14 способами, обратно – так же, тогда по правилу умножения: 14 * 14 = 196 способов. в) Сколько различных способов совершить путешествие из A в C и обратно так, чтобы обратный путь отличался от прямого хотя бы одним элементом? Мы можем попасть в С 14 способами, а обратно – 13, так как путь должен отличаться от того, по которому мы пришли: 14 * 13 = 182 способов. 4) а) Сколько палиндромов из 5 и 6 символов существует, если любой символ может использоваться больше двух раз: В палиндроме мы можем поставить на место первого, второго и третьего символа что угодно (к примеру, будем использовать латиницу – 26 символов), тогда четвертый, пятый (и шестой для палиндрома длиной 6) будут уже определены и неизменны, тогда по правилу умножения имеем: 26 * 26 * 26 = 17576 палиндромов длины 5 или 6, итого получается 35152 палиндрома длины 5 и 6 символов. б) Сколько палиндромов из 5 и 6 символов существует, если любой символ может использоваться не более двух раз: В этом случае мы может на место первого символа поставить 26 букв, второго – 25, а третьего – 24, так как в палиндроме не может использоваться менее чем две одинаковых буквы: 26 * 25 * 24 = 15600 палиндромов, это 31200 палиндромов длины 5 и 6 символов. 5) Существует ли трехзначное число abc в десятичной системе счисления (100a + 10b + c) такое, что abc = a! + b! + c!?  Программа выдает ответ – 145 (1! + 4! + 5! = 1 + 24 + 120 = 145). 6) а) Сколькими способами можно выбрать 5 игроков в команде из 12 человек? 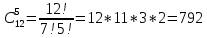 б) Если в нее включаются сильнейший и слабейший игрок: Два места заняты двумя игроками, значит: 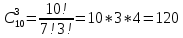 7) Найти 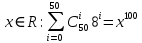 : :Согласно биному Ньютона: 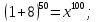 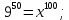 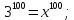 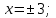 8) Найти: 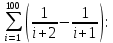 Если раскрыть эту сумму, то большинство дробей взаимоуничтожатся, останутся только первая и последняя: 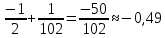 9) Разработать программу, генерирующую выборки размера 3 из {1, 2, 3, 4, 5, 6}: 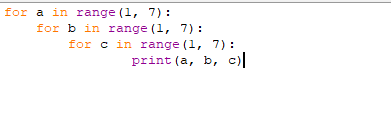 10) а) Сколько неотрицательных целых решений имеет система уравнений: 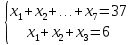  Программа возвращает значение 167552 б) Сколько при положительных x1, x2, x3?  Программа возвращает значение 59840 11) Сколькими способами можно выбрать n объектов из 2n, среди которых n одинаковых и n различных? Так как задание не совсем понятно, рассмотрим два случая: когда порядок имеет значение и когда не имеет: Если порядок не имеет значение, то будем рассматривать по отдельности выборки, в которых k одинаковых объектов, а остальные n - k – разные, тогда количество таких выборок для k будет равно 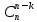 . .Теперь мы можем просуммировать от k = 0 до k = n и получим 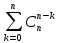 . .Если порядок имеет значение, то решаем аналогично, однако каждую получившую выборку надо умножить на число перестановок n!. 12) Сгенерировать все целочисленные решения: 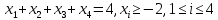 : : Программа вернула все решения и количество решений – 455. 13) Сколькими способами можно распределить 12 яблок между 5 детьми, чтобы никто не получил больше 7: 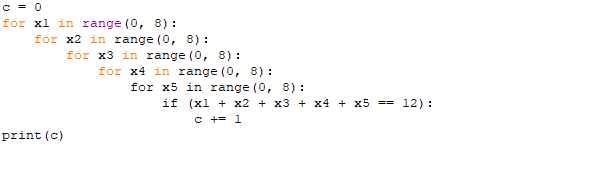 Программа возвращает значение 1470. |
