ЧИсленные методы решения линейных уравнений. ЛБ1 Нургалиев Р.М. Лабораторная работа 1 (ат02) Численные методы решения нелинейных уравнений студент Нургалиев Р. М. Преподаватель Круглов В. Н
 Скачать 228.04 Kb. Скачать 228.04 Kb.
|
|
Лабораторная работа №1 (АТ-02) Численные методы решения нелинейных уравнений Выполнил: студент Нургалиев Р.М. Преподаватель: Круглов В.Н. Введение В данной лабораторной работе требуется решить кубическое уравнение методом деления отрезка пополам и методом Ньютона и написать программу. Рисунок 1. Пример Программа была написана на языке Python. В качестве IDE был использован Visual Studio Code. В ходе решения, мы построили график и определили примерные координаты точки пересечения. 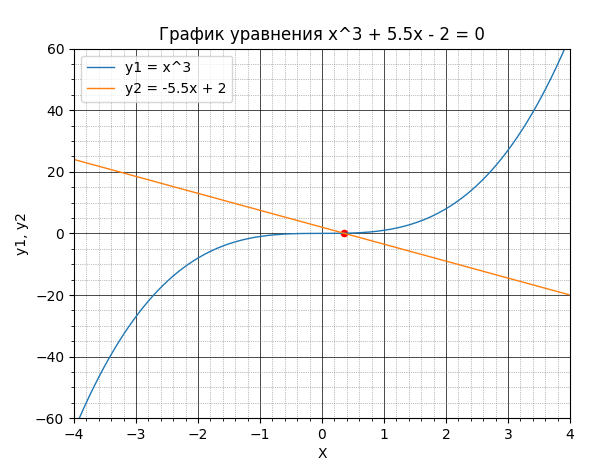 Рисунок 2. График Примерные координаты точки пересечения: [0.3554696928] [0.1113257678] Метод деления отрезка пополам Суть метода деления отрезка пополам состоит в разбиении отрезка [a, b] (при условии f(a)f(b) < 0) на два отрезка, определении знака функции f(х) в середине отрезка (a + b)/2 и выборе отрезка, на котором функция меняет знак и содержит решение. Деление отрезка продолжается до достижения необходимой точности решения e. Сначала находим отрезок [a, b] такой, что функция f(x) непрерывна и меняет знак на отрезке, то есть f(a)-f(b) < 0. На данном рисунке(3) написан алгоритм деления отрезков пополам. 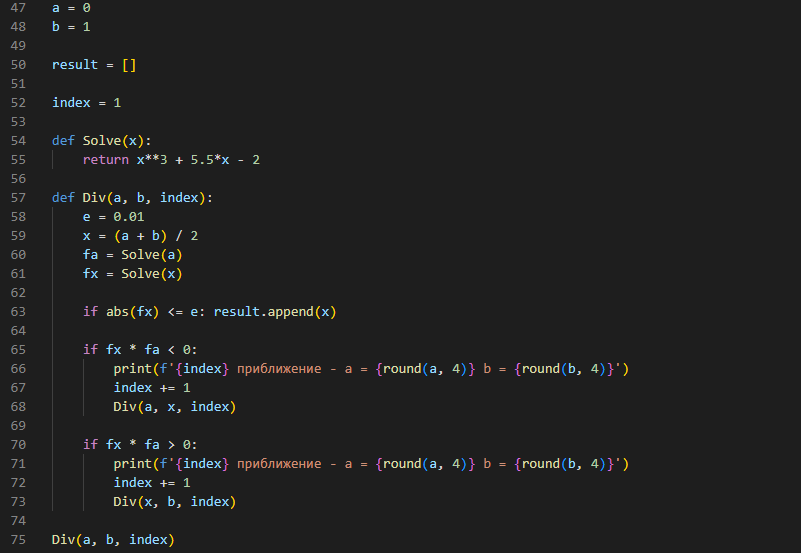 Рисунок 3. Метод деления пополам На рисунке(4) написана функция F(x)=x^3+5.5x-2. Рисунок 4. Функция возвращающая ответ ответ программы. Тут мы можем наблюдать часть итераций алгоритма. После которых, следует 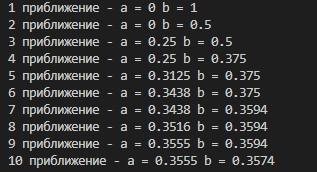 Рисунок 5. Приближения Рисунок 6. Ответ Метод Ньютона В данном алгоритме мы реализовали функцию, которая сначала определяет производные. Затем проверяет условие сходимости интервала. А после этого, с помощью цикла, находим нужное нам приближение. 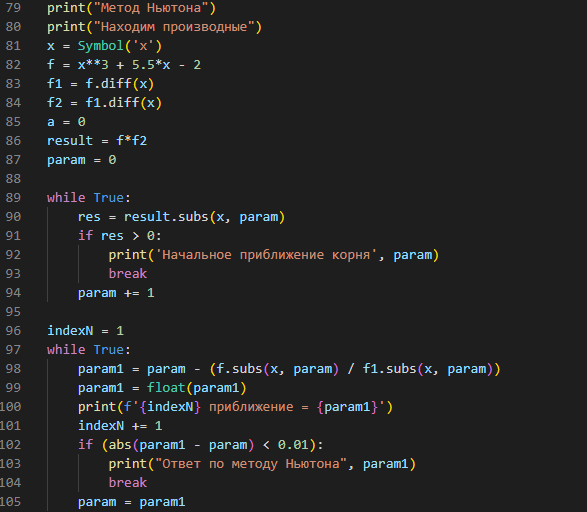 Рисунок 7. Алгоритм метода Ньютона 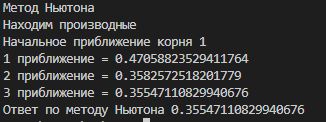 Рисунок 8. Ответ метода Ньютона Проверка Метод Ньютона был проверен, с помощью онлайн калькулятора (https://math.semestr.ru/optim/dichotomy-minimum.php). Ответ на сайте совпадает с решением нашей программы. 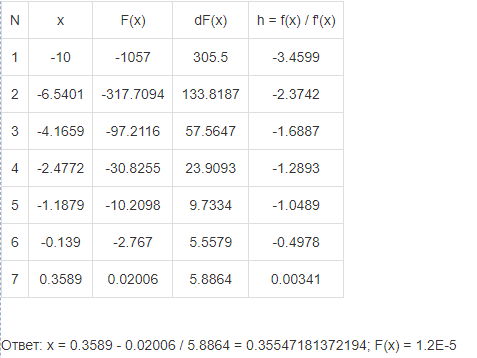 Рисунок 9. Проверка Ньютона Метод деления отрезка пополам также был проверен, с помощью онлайн калькулятора (https://math.semestr.ru/optim/newton.php). Ответ на сайте также совпадает с решением нашей программы. 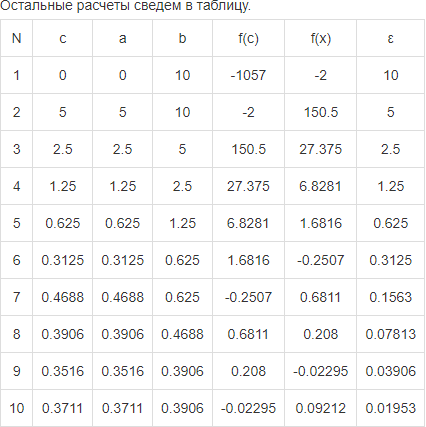  Рисунок 10. Проверка метода деления отрезка Вывод В ходе данной лабораторной работы, мы решили уравнение графическим методом, нашли примерные координаты точки пересечения: [0.3554696928] [0.1113257678]. Уточнили корень методом деления отрезка пополам и методом Ньютона. Написали программу алгоритма, и проверили её работу. В ответе получили примерное значение х=0,355. Проверили наше решение на онлайн ресурсе. Ответы совпали. |
