Системы автоматического управления. Лабораторная работа 1 Цель работы
 Скачать 234 Kb.
|
|
Лабораторная работа № 1 Цель работы: построить график переходной функции объекта и определить длительность переходного процесса, возникающего при подаче на его вход ступенчатого единичного воздействия. Теоретические положения Системы автоматического управления (САУ) подразделяются на два основных вида: разомкнутые и замкнутые. В разомкнутых САУ (рис. 1) сигнал на выходе управляемого объекта   Рис. 1. Разомкнутая САУ. не измеряется, т.е. отсутствует контроль за состоянием объекта в различные моменты времени  . Поэтому в них управление выходным сигналом осуществляется путем изменения сигнала задания  . При этом возникает переходный процесс, т.е. сигнал не мгновенно повторяет изменение сигнала , а постепенно приближается к нему. Процесс изменения со временем выходного сигнала , обусловленный изменением сигнала задания , называется переходным процессом. Переходные процессы характеризуются длительностью  , т.е. интервалом времени от начала переходного процесса до момента, когда отклонение выходной величины от ее нового установившегося значения становится меньше определенной достаточно малой величины. Обычно в качестве последней берут 5 % максимального отклонения в переходный период.Длительность переходного процесса характеризует быстродействие системы. Для сравнения быстродействия различных систем используют так называемые переходные характеристики, выражающие зависимость от времени выходного сигнала системы при подаче на ее вход сигналов специального вида. Если на вход разомкнутой системы (управляемого объекта) подается единичное ступенчатое воздействие 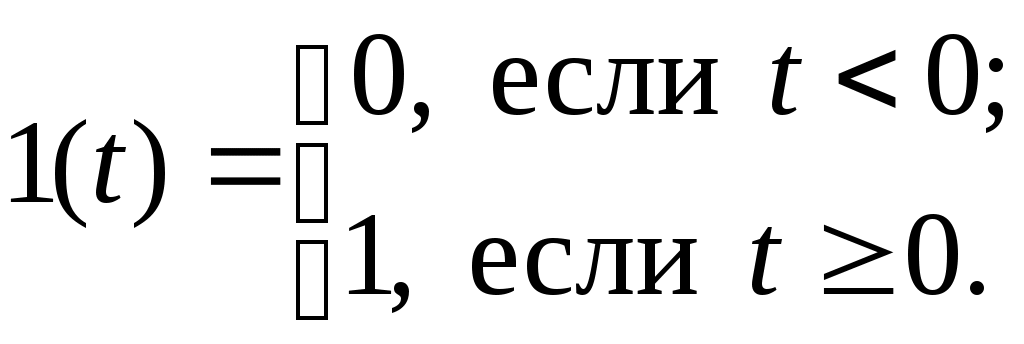 , то выходной сигнал  принято называть переходной функцией. Воздействие описывается следующим выражением: (1.1)Таким образом, - это выражение для при  , (1.2)т.е. реакция управляемого объекта на единичное ступенчатое воздействие. Переходную функцию объекта можно определить теоретически, если известны математические соотношения, устанавливающие взаимосвязь между сигналами и . Для математического описания данной взаимосвязи часто используют дифференциальные уравнения следующего вида:  , (1.3)где  и  - целые положительные числа ( );  и  - постоянные коэффициенты. Решая уравнение (1.3) в предположении, что выполняются равенства (1.1) и (1.2), определим переходную функцию объекта , т.к. в этом случае  .Однако гораздо более наглядным и физически ясными являются методы математического описания объектов и систем управления, базирующиеся на аппарате передаточных функций и частотных характеристик. Применив к уравнению (1.3) интегральное преобразование Лапласа  , (1.4)перейдем от дифференциального уравнения к алгебраическому 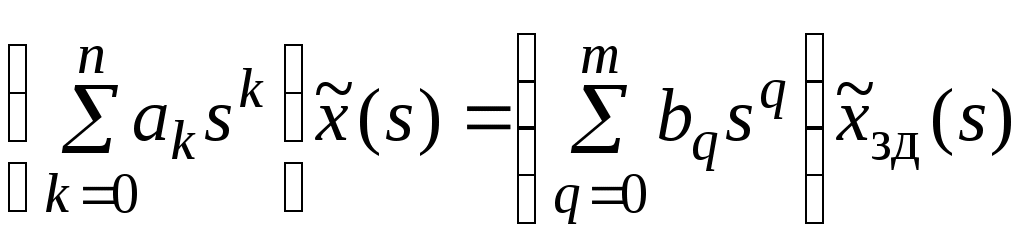 , (1.5)где  и  - изображения по Лапласу сигналов и соответственно, т.е.  ;  .Величина  в равенствах (1.4) и (1.5) является комплексным числом.Отношение  принято называть передаточной функцией объекта  в разомкнутой системе управления, т.е. . (1.6)Согласно выражениям (1.5) и (1.6) имеем 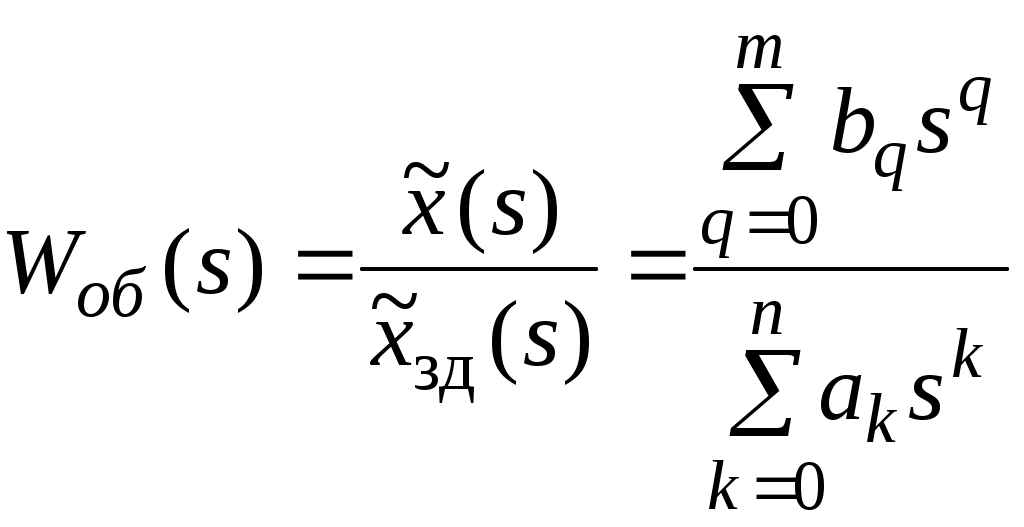 . (1.7)От передаточных функций легко перейти к комплексным частотным характеристикам (КЧХ). Для этого в выражении для передаточной функции (1.7) необходимо комплексный аргумент 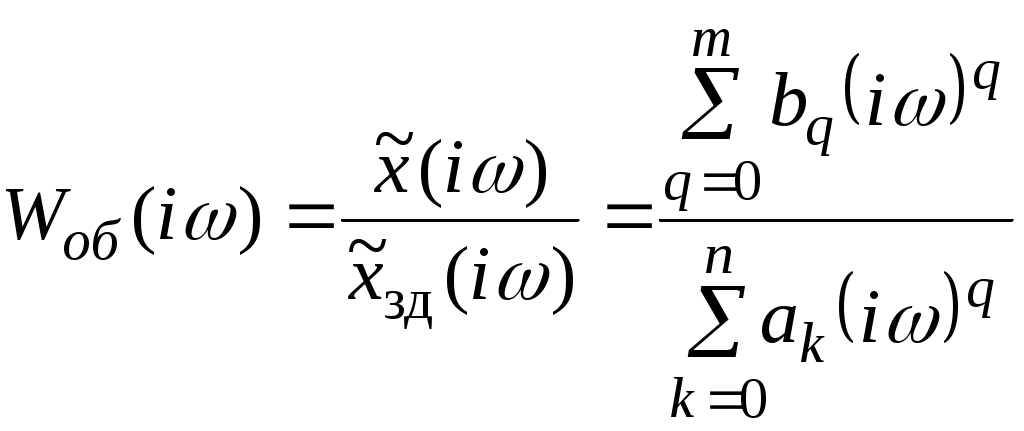заменить на  , где  - мнимая единица, а  - циклическая частота. Выполнив данную замену, получим . (1.8)Взаимосвязь между КЧХ объекта  и его переходной функцией устанавливается следующим выражением: . (1.9)На основании (1.9) можно установить связь между предельным значением переходной функции объекта   и значением его КЧХ при нулевой частоте, а именно  . (1.10)Равенство (1.10) можно использовать при определении длительности переходных процессов. Действительно, длительность переходного процесса определяется из условия . (1.11)В таком случае из равенства (1.11) установим, что  . (1.12)Подставляя выражение (1.10) в (1.12) имеем  . (1.13)Следовательно, чтобы определить значение достаточно построить график переходной функции , воспользовавшись для этого выражением (1.9), а затем провести на нем параллельно оси времени прямую  . В точке пересечения графика и прямой опустить перпендикуляр на временную ось. Временной интервал от начала системы координат до точки пересечения указанного перпендикуляра и временной оси определяет значение величины .Задание Рассмотрим разомкнутую САУ, представленную на рис. 1. Передаточную функцию управляемого объекта зададим выражением , (1.14)где  - коэффициент передачи объекта;  ,  и  - постоянные времени объекта, называемые параметрами объекта. Тогда, выполнив в выражении (1.14) замену  , получим выражение для КЧХ объекта . (1.15)Подставив в выражение (1.15) значение  установим, что . (1.16)Воспользовавшись выражениями (1.9) и (1.15) необходимо расчетным путем определить значения переходной функции и построить ее график. Затем, на основании выражений (1.13) и (1.16) следует определить по этому графику длительность переходного процесса .Значения параметров исследуемых объектов представлены в таблице 1. Параметры объектов. Таблица 1
Номер исследуемого объекта в таблице 1 студент определяет по последней цифре своего шифра. Если эта цифра окажется нулем, то следует выбрать объект № 10. Для расчета значений переходной функции выбранного объекта рекомендуется использовать, написанную на алгоритмическом языке Турбо Паскаль программу PERFUN1. В целях пояснения задания, которое студентам предстоит выполнить, рассмотрим пример. Пример. Пусть параметры исследуемого объекта с передаточной функцией (1.14) принимают следующие значения:   ;  ;  ;  . (1.17)Тогда согласно равенствам (1.15), (1.16) и (1.17) установим, что  . (1.18)Введя значения (1.17) в программу PERFUN1 и задавая затем различные моменты времени рассчитаем значения переходной функции объекта (1.14), (1.17). На основании результатов расчета построен график функции 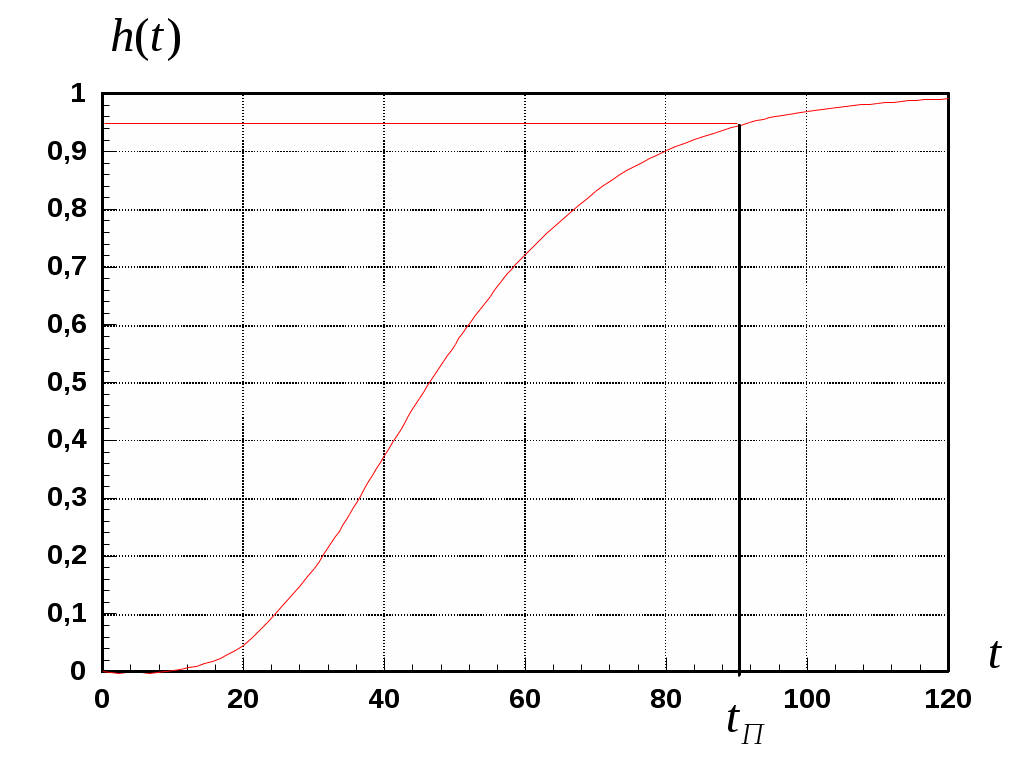, представленный на рис. 2. Рис. 2. Переходная функция объекта. По данному графику на основании равенств (1.13) и (1.18) установим, что  . |
