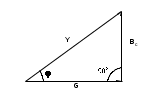МУ_ЛР-1. Лабораторная работа 1 Цепи синусоидального тока с резисторами, конденсаторами и катушками индуктивности

• Название: Лабораторная работа 1 Цепи синусоидального тока с резисторами, конденсаторами и катушками индуктивности
• Дата: 09.04.2022
• Размер: 366.8 Kb.
• Имя файла: МУ_ЛР-1.docx
• Тип: Лабораторная работа; #458115

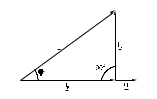
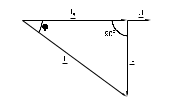
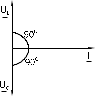
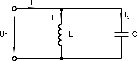
Последовательное соединение резистора и конденсатора

Лабораторная работа № 1

Цепи синусоидального тока с резисторами, конденсаторами и катушками индуктивности

Эксперименты данного раздела касаются взаимодействия резисторов, конденсаторов и катушек индуктивности при переменном синусоидальном напряжении.

Цель состоит в измерении и расчете токов, напряжений и их фазовых сдвигов, также как и эквивалентных параметров цепей при параллельном и последовательном соединении резисторов, конденсаторов и катушек.

Действующие значения и фазы соответствующих величин могут быть показаны на векторных диаграммах или на осциллограммах.

На векторной диаграмме каждая синусоидальная функция времени (ток или напряжение) представляется вектором, длина которого соответствует в выбранном масштабе амплитуде или действующему значению, а направление определяется начальной фазой, отсчитываемой от выбранного начала отсчета углов. Например, напряжение u = U_m sin (t+) изображается вектором длиной U_m или U_m/2, расположенным под углом  к горизонтали. Векторные изображения синусоидальных величин в дальнейшем будут подчеркиваться.

1. Последовательное соединение резистора и конденсатора

1.1. Общие сведения

Когда к цепи (рис. 1.1а) с последовательным соединением резистора и конденсатора подается переменное синусоидальное напряжение, один и тот же синусоидальный ток имеет место в обоих компонентах цепи.



б


а

Рис. 1.1
Между напряжениями U_R, U_C и U существуют фазовые сдвиги, обусловленные емкостным реактивным сопротивлением X_C конденсатора. Они могут быть представлены с помощью векторной диаграммы напряжений (рис. 1.1б)

Фазовый сдвиг между током I и напряжением на резисторе U_R отсутствует, тогда как сдвиг между этим током и падением напряжения на конденсаторе U_C равен -90⁰ (т.е. ток опережает напряжение на 90⁰). При этом сдвиг между полным напряжением цепи U и током I определяется соотношением между сопротивлениями X_C и R.

Если каждую сторону треугольника напряжений разделить на ток, то получим треугольник сопротивлений (рис.1.2). В треугольнике сопротивлений Z представляет собой так называемое полное сопротивление цепи.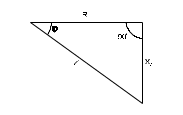




Рис. 1.2
Из-за фазового сдвига между током и напряжением в цепях, подобных данной, простое арифметическое сложение действующих или амплитудных значений напряжений на отдельных элементах цепи невозможно. Невозможно и сложение разнородных (активных и реактивных) сопротивлений. Однако, в векторной форме

U = U_R +U_C.
Действующее значение полного напряжения цепи, как следует из векторной диаграммы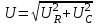
= Z  I
Полное сопротивление цепи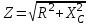
= U  I
Активное сопротивление цепи
R = Z  cos 
Емкостное реактивное сопротивление цепи
X_C = Z  sin 
Угол сдвига фаз
 = arctg (-U_C  U_R) = arctg (-Х_C  R)

1.2. Экспериментальная часть

Задание
Для цепи с последовательным соединением резистора и конденсатора измерьте и вычислите действующие значения падений напряжения на резисторе U_R и конденсаторе U_C, ток I, угол сдвига фаз , полное сопротивление цепи Z и емкостное реактивное сопротивление X_C и активной сопротивление R.
Порядок выполнения работы

• 
  Соберите цепь согласно схеме (рис. 1.3), подсоедините регулируемый источник синусоидального напряжения и установите его параметры: U = 5 В, f = 1 кГц.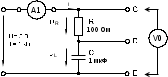
  

Рис. 1.3

• 
  Выполните мультиметрами или виртуальными приборами измерения действующих значений тока и напряжений, указанных в табл. 1.1. При измерениях напряжений подключайте мультиметр или канал V0 коннектора к зажимам C-E, C-D, D-E:
  

Таблица 1.1.

U, B	UR, B	UC, B	I, мА	, град	R, Ом	XC, Ом	Z, Ом	Примечание
								Расчет
								Вирт. Изм

• 
  Вычислите:
  

Фазовый угол

 = arctg (U_C  U_R) =
Полное сопротивление цепи

Z = U  I =
Активное сопротивление цепи

R = Z cos 
Емкостное реактивное сопротивление цепи

X_C = Z sin 

• 
  Если вы работаете с виртуальными приборами, то измерьте с помощью блока «Приборы II» R, , X_C, Z и запишите их значения также в таблицу 1.1 под рассчитанными величинами. Сравните результаты.
  

• 
  Выберите масштабы и постройте векторную диаграмму напряжений и треугольник сопротивлений на миллиметровой бумаге.
  

2. Параллельное соединение резистора и конденсатора

2.1. Общие сведения

Когда к цепи (рис. 2.1) с параллельным соединением резистора и конденсатора подается переменное синусоидальное напряжение, одно и то же напряжение приложено к обоим компонентам цепи.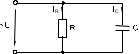



Рис. 2.1
Общий ток цепи I разветвляется на ток в конденсаторе I_C (емкостная составляющая общего тока) и ток в резисторе I_R (активная составляющая).

Между токами I, I_C и I_R существуют фазовые сдвиги, обусловленные емкостным реактивным сопротивлением X_C конденсатора. Они могут быть представлены с помощью векторной диаграммы токов (рис. 2.2а).

а	б
Рис. 2.2

Фазовый сдвиг между напряжением U цепи и током в резисторе I_R отсутствует, тогда как между этим напряжением и током в конденсаторе I_C равен –90⁰ (т.е. ток опережает напряжение на 90⁰). При этом сдвиг между полным током Iи напряжением U цепи определяется соотношением между проводимостями B_C и G. Разделив каждую сторону треугольника токов на напряжение, получим треугольник проводимостей (рис. 2.2 б).

В треугольнике проводимостей:

G=1/R – активная проводимость, [См].

B_C=1/X_C – реактивная (емкостная) проводимость, [См].

Y - представляет собой так называемую полную проводимость цепи, [См].

Из-за фазового сдвига между током и напряжением в цепях, подобных данной, простое арифметическое сложение действующих или амплитудных токов в параллельных ветвях невозможно. Но в векторной форме:

I = I_R +I_C.

Расчет ведется по следующим формулам, вытекающим из векторной диаграммы и треугольника проводимости:
Действующее значение полного тока цепи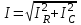

; I = U  Z = UY.
Полная проводимость цепи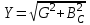

; Y = I U = 1/Z ,

где Z - полное сопротивление цепи.
Угол сдвига фаз

 = arctg (I _C  I_R) = arctg (B_C  G).
Активная и реактивная проводимости

G = Y cos; B_C = Y sin.

2. Экспериментальная часть

Задание
Для цепи с параллельным соединением резистора и конденсатора измерьте действующие значения тока в резисторе I_R и конденсаторе I _C, полный ток I и вычислите угол сдвига фаз , полное сопротивление цепи Z и емкостную реактивную проводимость B_C.
Порядок выполнения работы

• 
  Соберите цепь согласно схеме (рис. 2.3), подсоедините регулируемый источник синусоидального напряжения и установите его параметры: U = 5 В, f = 1 кГц.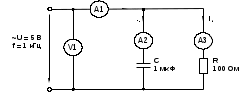
  

Рис. 2.3

• 
  Выполните измерения U, I, I_C, I_R и занесите результаты в табл. 2.1. Если измерения производите виртуальными приборами, то измерьте также R, , X_C, Z.
  

Таблица 2.1

U, B	I, мА	IС, мА	IR, мА	, град	R, Ом	XC, Ом	Z, Ом	Примечание
								Расчет
								Вирт. Изм

• 
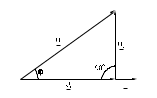
  Вычислите и запишите в таблицу:
  

Фазовый угол

 = arctg (I _C  I _R) =
Активные проводимость цепи и сопротивление цепи
G = I_R  U ; R = U  I_R.
Емкостные реактивные проводимость и сопротивление цепи
B_C = I_C  U ; X_C = U  I_C.
Полные проводимость и сопротивление цепи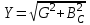
; Z = 1  Y.

• 
  Сравните результаты вычислений с результатами виртуальных измерений (если они есть).
  

• 
  Постройте векторную диаграмму токов и треугольник проводимостей в масштабе на миллиметровой бумаге.
  

3. Последовательное соединение резистора и катушки индуктивности

3.1. Общие сведения

Когда к цепи (рис. 3.1) с последовательным соединением резистора и катушки индуктивности подается переменное синусоидальное напряжение, один и тот же синусоидальный ток имеет место в обоих компонентах цепи.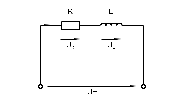




Рис. 3.1
Между напряжениями U_R, U_L и U существуют фазовые сдвиги, обусловленные индуктивным реактивным сопротивлением X_L катушки. Они могут быть представлены с помощью векторной диаграммы напряжений (рис. 3.2а).

а	б
Рис. 3.2

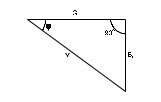
Фазовый сдвиг между током I и напряжением на резисторе U_R отсутствует, тогда как сдвиг между этим током и падением напряжения U_L на катушке индуктивности равен 90⁰ (ток отстает от напряжения). При этом сдвиг между полным напряжением U цепи и током определяется соотношением между сопротивлениями X_L и R. Разделив все стороны треугольника напряжений на ток, получим треугольник сопротивлений (рис. 3.2 б), в котором Z представляет собой так называемое полное сопротивление цепи.

Из-за фазового сдвига между током и напряжением в цепях, подобных данной, простое арифметическое сложение напряжений на отдельных элементах как в последовательной чисто резистивной цепи, невозможно. Только в векторной форме U = U_R +U_L. Расчет ведется по следующим формулам, вытекающим из векторной диаграммы и треугольника сопротивлений.
Действующее значение полного напряжения цепи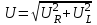


U = Z  I
Полное сопротивление цепи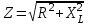
;

Z = U  I
Активное сопротивление цепи
R = Z  cos 
Индуктивное реактивное сопротивление цепи
X_L = Z  sin 
Угол сдвига фаз
 = arctg (Х_L  R)

3.2. Экспериментальная часть

Задание
Для цепи с последовательным соединением резистора и катушки индуктивности измерьте действующие значения падений напряжения на резисторе U_R и катушке U_L и ток I. Вычислите фазовый угол , полное сопротивление цепи Z, индуктивное реактивное сопротивление X_L и фазовый сдвиг между полным напряжением цепи U и падением напряжения на катушке U_L. Активным сопротивлением катушки ввиду его малой величины можно при этом пренебречь.
Порядок выполнения работы

• 
  Соберите цепь согласно схеме (рис. 3.3), подсоедините регулируемый источник синусоидального напряжения и установите его параметры: U = 5 В, f = 200 Гц. В качестве индуктивности с малым активным сопротивлением используйте катушку трансформатора 300 витков, вставив между подковами разъемного сердечника полоски бумаги в один слой (немагнитный зазор).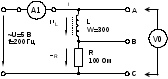
  

Рис. 3.3

• 
  Выполните измерения тока и напряжений, указанных в табл. 3.1. Если измерения производятся виртуальными приборами, то измерьте также R, , X_L, Z.
  

Таблица 3.1.

U, B	UL, B	UC, B	I, мА	, град	R, Ом	XL, Ом	Z, Ом	Примечание
								Расчет
								Вирт. Изм

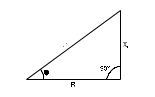
Вычислите  = arctg (U_L  R), Z = U  I, X_L = U_L  I, занесите результаты вычислений в табл. 3.1 и сравните с результатами виртуальных измерений, если они есть.

• 
  Выберите масштабы и постройте векторную диаграмму напряжений и треугольник сопротивлений на миллиметровой бумаге.
  

4. Параллельное соединение резистора и катушки индуктивности

4.1. Общие сведения

Когда к цепи (рис. 4.1) с параллельным соединением резистора и катушки подается переменное синусоидальное напряжение, одно и то же напряжение приложено к обоим компонентам цепи.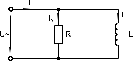



Рис. 4.1
Общий ток цепи I разветвляется на ток в катушке I_L (индуктивная составляющая общего тока) и ток в резисторе I_R (активная составляющая).

Между токами I, I_L и I_R существуют фазовые сдвиги, обусловленные индуктивным реактивным сопротивлением X_L катушки. Они могут быть представлены с помощью векторной диаграммы токов (рис. 4.2а).

а	б
Рис.4.2

Фазовый сдвиг между напряжением U цепи и током в резисторе I_R отсутствует, тогда как ток в катушке I_L всегда отстает от напряжения цепи (или тока в резисторе I_R) на 90⁰. При этом сдвиг между полным током I и напряжением цепи U определяется соотношением между проводимостями B_L и G.

Разделив каждую сторону треугольника токов на напряжение, получим треугольник проводимостей (рис. 4.2 б), в котором Y представляет собой так называемую полную проводимость цепи, G – активную, а B_L – реактивную (индуктивную) проводимости.

Из-за фазового сдвига между током и напряжением в цепях, подобных данной, простое арифметическое сложение действующих или амплитудных значений токов в параллельных ветвях, как в параллельной чисто резистивной цепи, невозможно. Только в векторной форме I = I_R +I_L. Расчет ведется по следующим формулам:

Действующее значение полного тока цепи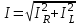
,

I = U  Z = UY .
Полная проводимость цепи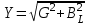
,

Y = 1  Z ,
где Z - полное сопротивление цепи.
Угол сдвига фаз
 = arctg (I _L  I_R) = arctg (B_L  G).
Активное сопротивление цепи

G = Y  cos \
Реактивное сопротивление цепи

B = Y  sin .

4.2. Экспериментальная часть

Задание
Для цепи с параллельным соединением резистора и катушки индуктивности измерьте действующие значения тока в резисторе I_R и катушке I_L, полный ток I и вычислите угол сдвига фаз , полное сопротивление цепи Z и индуктивную реактивную проводимость B_L.
Порядок выполнения работы

• 
  Соберите цепь согласно схеме (рис. 4.3), подсоедините регулируемый источник синусоидального напряжения и установите его параметры: U = 5 В, f = 200 Гц. В качестве индуктивности с малым активным сопротивлением используйте катушку трансформатора 300 витков, вставив между подковами разъемного сердечника полоски бумаги в один слой (немагнитный зазор).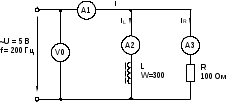
  

Рис. 6.4.3

• 
  Выполните измерения U, I, I_L, I_R и занесите результаты в табл. 6.4.1. Если измерения производятся виртуальными приборами, то измерьте также R, , X_L, Z и вычислите G = 1/R, B_L = 1/X_L и Y = 1/Z. Занесите эти результаты в строку «виртуальные измерения» табл. 4.1.
  

Таблица .4.1.

U, B	I, мА	IL, мА	IR, мА	, град	G, 1/Ом	BL, 1/Ом	Y, 1/Ом	Примечание
								Расчет
								Вирт. изм

• 
  Вычислите  = arctg (I _L  I _R ); Y = I  U; G = I_R  U ; B_L = I_L  U.
  
• 
  Занесите результаты вычислений в таблицу и сравните с результатами измерений виртуальными приборами, если они есть.
  
• 
  Выберите масштабы и постройте векторную диаграмму напряжений и треугольник сопротивлений на миллиметровой бумаге.
  

5. Последовательное соединение конденсатора и катушки индуктивности. Понятие о резонансе напряжений

5.1. Общие сведения

Когда по цепи (рис. 6.5.1) с последовательным соединением конденсатора и катушки индуктивности протекает один и тот же синусоидальный ток I, напряжение на конденсаторе U_C отстает от тока I на 90⁰, а напряжение на катушке индуктивности U_L опережает ток на 90⁰. Эти напряжения находятся в противофазе (повернуты относительно друг друга на 180⁰).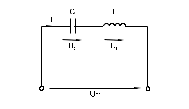



Рис. 5.1
Когда одно из напряжений больше другого, цепь оказывается либо преимущественно индуктивной (рис. 5.2а), либо преимущественно емкостной (рис. 5.2б). Если напряжения U_L и U_С имеют одинаковые значения и компенсируют друг друга, то суммарное напряжение на участке цепи L – C оказывается равным нулю. Остается только небольшая составляющая напряжения на активном сопротивлении катушки и проводов. Такое явление называется резонансом напряжений (рис. 5.3в).

а	б	в
Рис. 5.2

При резонансе напряжений реактивное сопротивление цепи
X = X_L – X_C

оказывается равным нулю. При заданных значениях L и C резонанс может быть получен путем изменения частоты.

Поскольку X_L = L, а X_C = 1 / C, то резонансная частота ₀ может быть определена из уравнения:

₀L – 1 / ₀C = 0,

откуда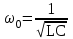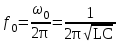



.
Полное сопротивление цепи при резонансе оказывается равным небольшому активному сопротивлению катушки, поэтому ток в цепи совпадает по фазе с напряжением и может оказаться довольно большим даже при маленьком приложенном напряжении. При этом напряжения U_L и U_C могут существенно (в десятки раз!) превышать приложенное напряжение.

5.2. Экспериментальная часть

Задание
Для цепи с последовательным соединением конденсатора и катушки индуктивности измерьте действующие значения тока I и напряжений U, U_C, U_L при  = ₀, <₀ и >₀. Постройте векторные диаграммы.
Порядок выполнения работы

• 
  Соберите цепь согласно схеме (рис. 5.3), подсоедините регулируемый источник синусоидального напряжения и установите напряжение на его входе 2 В и частоту 500 Гц. В качестве индуктивности с малым активным сопротивлением используйте катушку трансформатора 300 витков, вставив между подковами разъемного сердечника полоски бумаги в один слой (немагнитный зазор).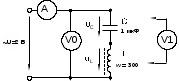
  

Рис. 5.3

• 
  Изменяя частоту приложенного напряжения, добейтесь резонанса по максимальному току. Для точной настройки по максимуму тока необходимо поддерживать неизменным напряжение на входе цепи. При измерениях виртуальными приборами резонанс настраивается по переходу через ноль угла сдвига фаз между входными напряжением и током. Тогда нет необходимости поддерживать входное напряжение неизменным.
  

• 
  Произведите измерения и запишите в табл. 5.1 результаты измерений при резонансе f=f₀ при f₁  0,75f₀ и f₂ 1,25f₀.
  

Таблица 5.1

f, Гц	I, мА	U, B	UL, B	UC, B
f0 =
f1 =
f2 =

• 
  Постройте в одинаковом масштабе векторные диаграммы для каждого из рассмотренных случаев.
  

6. Параллельное соединение конденсатора и катушки индуктивности.
Понятие о резонансе токов

6.1. Общие сведения

Когда к цепи (рис. 6.1) с параллельным соединением конденсатора и катушки индуктивности подается переменное синусоидальное напряжение U, одно и то же напряжение приложено к обоим элементам цепи.



Рис. 6.1
Общий ток цепи I разветвляется на ток в конденсаторе I_C (емкостная составляющая общего тока) и ток в катушке I_L (индуктивная составляющая общего тока), причем ток I_L отстает от напряжения U на 90⁰, а I_C опережает на 90⁰.

Токи I_C и I_L имеют противоположные фазы (180⁰) и в зависимости от их величин уравновешивают друг друга полностью или частично. Они могут быть представлены с помощью векторных диаграмм токов (рис. 6.2).

Когда I_C = I_L и общий ток цепи равен нулю, имеет место резонанс токов (векторная диаграмма рис. 6.2а)

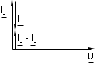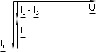а	б	в
Рис. 6.2

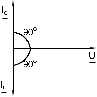
Когда I_C  I_L, т.е. преобладает ток конденсатора, общий ток цепи I является по характеру емкостным и опережает напряжение U на 90⁰ (рис. 6.2б).

Когда I_C I_L, т.е. преобладает ток катушки, общий ток цепи I является индуктивным и отстает от напряжения U на 90⁰ (рис. 6.2в).

Эти рассуждения проведены в пренебрежении потерями активной мощности в конденсаторе и катушке.

При резонансе токов реактивная проводимость цепи B = B_L – B_C равна нулю. Резонансная частота определяется из уравнения

,

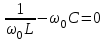откуда, так же, как и при резонансе напряжени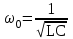й,
и .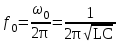
Полная проводимость при резонансе токов оказывается близкой к нулю. Остается нескомпенсированной лишь небольшая активная проводимость, обусловленная активным сопротивлением катушки и несовершенной изоляцией конденсатора. Поэтому ток в неразветвленной части цепи имеет минимальное значение, тогда как токи I_L и I_C могут превышать его в десятки раз.

6.2. Экспериментальная часть

Задание
Для цепи с параллельным соединением конденсатора и катушки индуктивности измерьте действующие значения напряжения U и токов I, I_C и I_L при  = ₀, <₀ и >₀. Постройте векторные диаграммы.
Порядок выполнения работы

• 
  Соберите цепь согласно схеме (рис. 6.3), подсоедините регулируемый источник синусоидального напряжения и установите его параметры: U = 7 В, f = 500 Гц. В качестве индуктивности с малым активным сопротивлением используйте катушку трансформатора 300 витков, вставив между подковами разъемного сердечника полоски бумаги в один слой (немагнитный зазор).
  

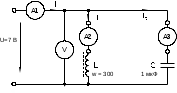
Рис. 6.3

• 
  Изменяя частоту приложенного напряжения, добейтесь резонанса по минимальному току I. Для точной настройки поддерживайте неизменным напряжение на входе цепи. При измерениях виртуальными приборами резонанс настраивается по переходу через ноль угла сдвига фаз между входным током и напряжением. Тогда необязательно поддерживать неизменным напряжение на входе цепи.
  
• 
  Произведите измерения и запишите результаты измерений в табл. 6.1 при f = f₀, f₁0,75f₀ и f₂ 1,25f₀.
  

Таблица 6.1

f, Гц	U, B	I, мА	IL, мА	IC, мА
f0 =
f1 =
f2 =

• 
  Постройте в одинаковом масштабе векторные диаграммы для каждого из рассмотренных случаев.
  

Контрольные вопросы.

1. 
   Записать выражения законов Ома и Кирхгофа для цепей переменного тока.
   

закон Ома для переменного тока: значение тока в цепи переменного тока прямо пропорционально напряжению в цепи и обратно пропорционально полному сопротивлению цепи.

,

2. 
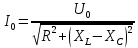   Каким образом осуществляется последовательное соединение элементов в электрической цепи?
   
3. 
   Каким образом осуществляется параллельное соединение элементов в электрической цепи?
   
4. 
   Записать формулы для определения индуктивного и емкостного сопротивлений.
   

Индуктивное сопротивление

.

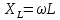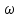– циклическая частота переменного тока (рад/с)

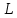– индуктивность (Гн)

Емкостное сопротивление

.

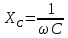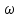– циклическая частота переменного тока (рад/с)

С – емкость проводника (Ф)

5. 
   Записать формулы для определения активной, реактивной и полной мощности цепи.
   

Активная мощность

P = UIcosφ

Реактивная мощность

Q = UIsinφ

Полная мощность

6. 
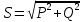
   Что такое резонанс напряжений? Условия возникновения резонанса напряжений? Изменением каких параметров электрической цепи можно обеспечить в ней режим резонанса напряжений?
   

Резонансом в электрических цепях называется режим участка электрической цепи, содержащей индуктивный и емкостной элементы, при котором разность фаз между напряжением и током равна нулю. Режим резонанса может быть получен при изменении частоты питающего напряжения или изменением параметров элементов L и С.

При последовательном соединении возникает резонанс напряжения.

7. 
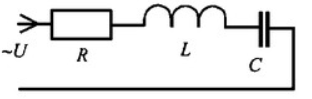
   Как определяются активная и реактивные проводимости?
   

Активная проводимость



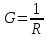
Реактивная проводимость

B = |B_L – B_C|

где 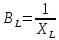– реактивная индуктивная проводимость

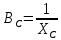– реактивная емкостная проводимость

8. 
   Что такое резонанс токов? Условия возникновения резонанса токов? Изменением каких параметров электрической цепи можно обеспечить в ней режим резонанса токов? Дайте примеры практического использования резонансных явлений в электрических цепях.
   

Режим электрической цепи при параллельном соединении участков с индуктивностью и емкостью, характеризующийся равенством индуктивной и емкостной проводимостей, называют резонансом токов.

Так же как и резонанс напряжений, резонанс токов возникает, когда частота источника энергии равна резонансной частоте.

Резонанс токов, так же как и резонанс напряжений, можно получить изменением параметров L и С или изменением частоты источника энергии.

9. 
   Правила подключения амперметра, вольтметра и ваттметра для измерения параметров электрических цепей.