Лабораторная работа 1 Институт 3 Системы управления, информатика и электроэнергетика

• Название: Лабораторная работа 1 Институт 3 Системы управления, информатика и электроэнергетика
• Дата: 06.10.2021
• Размер: 51.6 Kb.
• Имя файла: laba_1.docx
• Тип: Лабораторная работа; #242591

Московский Авиационный институт

(Национальный исследовательский университет)


Лабораторная работа № 1
Институт №3: «Системы управления, информатика и электроэнергетика»

Кафедра 304: «ВМ, системы, комплексы и сети»
«Нахождение безусловного экстремума»

Выполнил: Андреянов Никита Сергеевич

студент 324 группы 3 института:

Приняли: Григоревский Николай Владимирович

Москва 2021

Оглавление

Предварительные расчёты 2

Методы 2

Приложения 5

Приложение №1 5

Предварительные расчёты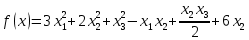

Сразу посчитаем все производные: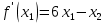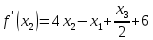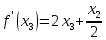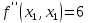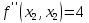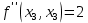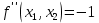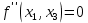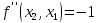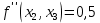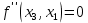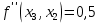

Методы

1)Аналитический: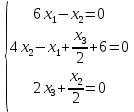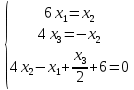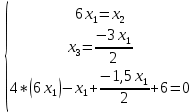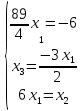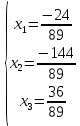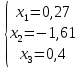





Проверка: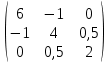



Считаем собственные значения методов вращения Якоби: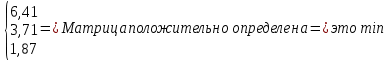

2)Градиентный: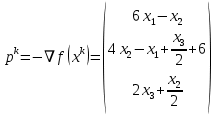



Пусть 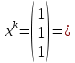далее был использован код [приложение 1]:

Результат:



3)Наискорейший спуска: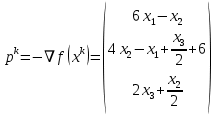



Пусть 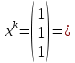далее был использован код [приложение 1]:



4)Гаусса-Зейделя: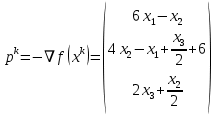



Пусть 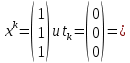далее был использован код[приложение 1]:

Данные такие же, как и в пункте 2.



5)Метод Ньютона: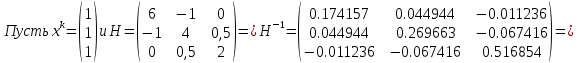

далее был использован код[приложение 1]:



6)Флетчера-Ривса: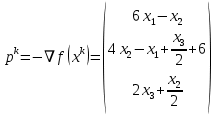



Пусть 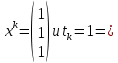далее был использован код[приложение 1]:

Приложения

Приложение №1

#define _CRT_SECURE_NO_WARNINGS
#include

#include

#include

#include

#include

#include
void gradient_alpha(double eps);//градиентный

void gradient_beta(double eps);//наискорейшего спуска

double f1_gradient(double* x);

double f2_gradient(double* x);

double f3_gradient(double* x);

double function(double* x);

void Gauss_Zeidel(double eps);//Гаусс-Зейдель

void Nuiwton(double eps);//Ньютона

double** create_H_reverse_matrix(double** matrix);

double* multiply(double** matrix, double* vector);

void Fletcger_Rivze(double eps);//Флетчер-Ривз

double Euclidean_norm(double* vector, int size_of_vector);
int main() {

system("color F0");

double eps = 0.01;

gradient_alpha(eps);

printf("\n");

gradient_beta(eps);

printf("\n");

Gauss_Zeidel(eps);

printf("\n");

Nuiwton(eps);

printf("\n");

Fletcger_Rivze(eps);

}
void gradient_alpha(double eps) {

int count = 0;//число итераций

int i, j;

double t_k = 1;//шаг

double x[3] = { 1,1,1 };//вектор

double p_k[3] = { 0 };

p_k[0] = -f1_gradient(x);

p_k[1] = -f2_gradient(x);

p_k[2] = -f3_gradient(x);

double f_x_k;

double f_x_k_next;

while (1) {

count++;

f_x_k = function(x);

double prom_x[3] = { 0 };//x^k+t_k*p^k

prom_x[0] = x[0] + t_k * p_k[0];

prom_x[1] = x[1] + t_k * p_k[1];

prom_x[2] = x[2] + t_k * p_k[2];

f_x_k_next = function(prom_x);

if (f_x_k > f_x_k_next) {

j = 0;

for (i = 0;i < 3;i++)

if (fabs(fabs(x[i]) - fabs(prom_x[i])) <= (eps*0.01))

j++;

if (j == 3) {

for (i = 0;i < 3;i++) printf("x[%d]=%f\n", i, x[i]);

printf("Number of inerations:%d\n", count);

return;

}

for (i = 0;i < 3;i++) x[i] = prom_x[i];

p_k[0] = -f1_gradient(x);

p_k[1] =- f2_gradient(x);

p_k[2] = -f3_gradient(x);

}

else {

t_k = t_k *eps;

}

}

}
void gradient_beta(double eps) {

int count = 0;//число итераций

int i, j;

double t_k = 1;//шаг

double x[3] = { 1,1,1 };//вектор

double p_k[3] = { 0 };

p_k[0] = -f1_gradient(x);

p_k[1] = -f2_gradient(x);

p_k[2] = -f3_gradient(x);

double f_x_k;

double f_x_k_next;

while (1) {

count++;

f_x_k = function(x);

double prom_x[3] = { 0 };//x^k+t_k*p^k

prom_x[0] = x[0] + t_k * p_k[0];

prom_x[1] = x[1] + t_k * p_k[1];

prom_x[2] = x[2] + t_k * p_k[2];

f_x_k_next = function(prom_x);

if (f_x_k > f_x_k_next) {

j = 0;

for (i = 0;i < 3;i++)

if (fabs(fabs(x[i]) - fabs(prom_x[i])) < (eps * 0.1))

j++;

if (j == 3) {

for (i = 0;i < 3;i++) printf("x[%d]=%f\n", i, x[i]);

printf("Number of inerations:%d\n", count);

return;

}

for (i = 0;i < 3;i++) x[i] = prom_x[i];

p_k[0] = -f1_gradient(x);

p_k[1] = -f2_gradient(x);

p_k[2] = -f3_gradient(x);

}

else {

t_k = 0;

double func = function(x);

while (1) {

t_k += eps*eps;

for (i = 0;i < 3;i++) prom_x[i] = x[i] + t_k * p_k[i];

if (function(prom_x) < func) func = function(prom_x);

else break;

}

}

}

}
double function(double* x) {

return 3 * x[0] * x[0] + 2 * x[1] * x[1] + x[2] * x[2] - x[0] * x[1] + x[1] * x[2] / 2 + 6 * x[1];

}
double f1_gradient(double* x) {

return 6 * x[0] - x[1];

}
double f2_gradient(double* x) {

return 4 * x[1] - x[0] + x[2] / 2 + 6;

}
double f3_gradient(double* x) {

return 2 * x[2] + x[1] / 2;

}
void Gauss_Zeidel(double eps) {

int count = 0;//число итераций

int i, j;

double t_k[3] = { 0,0,0 };//шаг

double x[3] = { 1,1,1 };//вектор

double p_k[3] = { 0 };

p_k[0] = -f1_gradient(x);

p_k[1] = -f2_gradient(x);

p_k[2] = -f3_gradient(x);

double f_x_k;

double f_x_k_next;

while (1) {

count++;

f_x_k = function(x);

double prom_x[3] = { 0 };//x^k+t_k*p^k

prom_x[0] = x[0] + t_k[0] * p_k[0];

prom_x[1] = x[1] + t_k[1] * p_k[1];

prom_x[2] = x[2] + t_k[2] * p_k[2];

f_x_k_next = function(prom_x);

if (f_x_k > f_x_k_next) {

j = 0;

for (i = 0;i < 3;i++)

if (fabs(fabs(x[i]) - fabs(prom_x[i])) <= (eps * 0.01))

j++;

if (j == 3) {

for (i = 0;i < 3;i++) printf("x[%d]=%f\n", i, x[i]);

printf("Number of inerations:%d\n", count);

return;

}

for (i = 0;i < 3;i++) x[i] = prom_x[i];

p_k[0] = -f1_gradient(x);

p_k[1] = -f2_gradient(x);

p_k[2] = -f3_gradient(x);

}

else {

for (j = 0;j < 3;j++) {

double func = function(x);

t_k[j] = 0;

while (1) {

t_k[j] += eps * eps;

prom_x[j] = x[j] + t_k[j] * p_k[j];

if (function(prom_x) < func) func = function(prom_x);

else break;

}

}

}

}

}
void Nuiwton(double eps) {

int count = 0;//число итераций

int i, j;

double x[3] = { 1,1,1 };//вектор

double* p_k =(double*)calloc(3,sizeof(double));

double** matrix = NULL;

matrix = (double**)calloc(3, sizeof(double*));

for (i = 0;i < 3;i++) matrix[i] = (double*)calloc(3, sizeof(double));

matrix[0][0] = 6; matrix[0][1] = -1;matrix[0][2] = 0;

matrix[1][0] = -1;matrix[1][1] = 4;matrix[1][2] = 0.5;

matrix[2][0] = 0;matrix[2][1] = 0.5;matrix[2][2] = 2;

matrix = create_H_reverse_matrix(matrix);

p_k[0] = f1_gradient(x);

p_k[1] = f2_gradient(x);

p_k[2] = f3_gradient(x);

double f_x_k;

double f_x_k_next;

while (1) {

count++;

f_x_k = function(x);

double prom_x[3] = { 0 };//x^k+t_k*p^k

p_k = multiply(matrix, p_k);

prom_x[0] = x[0] - p_k[0];

prom_x[1] = x[1] - p_k[1];

prom_x[2] = x[2] - p_k[2];

f_x_k_next = function(prom_x);

j = 0;

for (i = 0;i < 3;i++)

if (fabs(fabs(x[i]) - fabs(prom_x[i])) <= (eps * 0.01))

j++;

if (j == 3) {

for (i = 0;i < 3;i++) printf("x[%d]=%f\n", i, x[i]);

printf("Number of inerations:%d\n", count);

return;

}

for (i = 0;i < 3;i++) x[i] = prom_x[i];

p_k[0] = f1_gradient(x);

p_k[1] = f2_gradient(x);

p_k[2] = f3_gradient(x);

}

}
double** create_H_reverse_matrix(double** matrix) {

double _det_matrix_=0;

int i, j;

_det_matrix_ = matrix[1][1] * matrix[2][2] * matrix[0][0] + matrix[0][1] * matrix[1][2] * matrix[2][0] + matrix[1][0] * matrix[2][1] * matrix[0][2];

_det_matrix_ = _det_matrix_ - matrix[0][2] * matrix[1][1] * matrix[2][0] - matrix[0][1] * matrix[1][0] * matrix[2][2] - matrix[0][0] * matrix[1][2] * matrix[2][1];

double** rezerve = NULL;

rezerve = (double**)calloc(3, sizeof(double*));

for (i = 0;i < 3;i++) rezerve[i] = (double*)calloc(3, sizeof(double));

for (i = 0;i < 3;i++) {

for (j = 0;j < 3;j++) {

double a,b,c,d;

int n,//номер строки

m,//номер столбца

l,//номер столбца

k;//номер строки

if (i == 0) n = 1;

else n = 0;

if (j == 0) m = 1;

else m = 0;

if (i == 2) k = 1;

else k = 2;

if (j == 2) l = 1;

else l = 2;

rezerve[i][j] = ((i+j)%2?-1:1)*(matrix[n][m] * matrix[k][l] - matrix[n][l] * matrix[k][m]);

}

}

for (i = 0;i < 3;i++) for (j = 0;j < 3;j++) rezerve[i][j] = rezerve[i][j] / _det_matrix_;

return rezerve;

}
double* multiply(double** matrix,double* vector) {

double* rezerve = (double*)calloc(3, sizeof(double));

for (int i=0;i < 3;i++) rezerve[i] = 0;

for (int i = 0;i < 3;i++) {

for (int j = 0;j < 3;j++)

rezerve[i] += matrix[i][j] * vector[j];

}

return rezerve;

}
void Fletcger_Rivze(double eps) {

int count = 0;//число итераций

int i, j;

double t_k = 1;//шаг

double x[3] = { 1,1,1 };//вектор

double p_k[3] = { 0 };

double rezerve[3] = { 0 };

double f_x_k;

double f_x_k_next;

double norma_1,//||f(x^k)||

norma_2;//||f(x^(k-1)||

while (1) {

//d=-g_x, где d=


p_k[0] = -f1_gradient(x);

p_k[1] = -f2_gradient(x);

p_k[2] = -f3_gradient(x);

count++;

double prom_x[3] = { 0 };

//found r(t_k)

while (1) {

f_x_k = function(x);

prom_x[0] = x[0] + t_k * p_k[0];

prom_x[1] = x[1] + t_k * p_k[1];

prom_x[2] = x[2] + t_k * p_k[2];

f_x_k_next = function(prom_x);

if (f_x_k < f_x_k_next) t_k *= eps;

else break;

}

//s=r*d, где d=


for (i = 0;i < 3;i++) rezerve[i] = p_k[i] * t_k;

//x=x+s

for (i = 0;i < 3;i++) x[i] = prom_x[i];

//||g_x||

norma_1 = Euclidean_norm(p_k,3);

//g_y

prom_x[0] = - f1_gradient(x);

prom_x[1] = - f2_gradient(x);

prom_x[2] = - f3_gradient(x);

//||g_y||

norma_2 = Euclidean_norm(prom_x, 3);

for (i = 0;i < 3;i++) p_k[i] = prom_x[i] + p_k[i] * norma_1 / norma_2;

if (Euclidean_norm(rezerve, 3) < (eps*0.01)) {

for (i = 0;i < 3;i++) printf("x[%d]=%f\n", i, x[i]);

printf("Number of inerations:%d\n", count);

return;

}

count++;

}

}
double Euclidean_norm(double* vector,int size_of_vector) {

double result = 0;

for (int i = 0;i < size_of_vector;i++) result += vector[i] * vector[i];

result = sqrt(result);

return result;

}