Матметоды в инж расчетах. Исламов И.Р. БТК-19-01 ЛР-1. Лабораторная работа 1 Интерполяция и аппроксимация экспериментальных данных Вариант 7 (57)

• Название: Лабораторная работа 1 Интерполяция и аппроксимация экспериментальных данных Вариант 7 (57)
• Анкор: Матметоды в инж расчетах
• Дата: 01.12.2021
• Размер: 405.63 Kb.
• Имя файла: Исламов И.Р. БТК-19-01 ЛР-1.docx
• Тип: Лабораторная работа; #287496

Министерство науки и высшего образования Российской Федерации

ФЕДЕРАЛЬНОЕ ГОССУДАРСТВЕННОЕ БЮДЖЕТНОЕ
ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ
«УФИМСКИЙ ГОСУДАРСТВЕННЫЙ НЕФТЯНОЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»

Кафедра «ГМХТП»

Лабораторная работа №1

«Интерполяция и аппроксимация экспериментальных данных»

Вариант 7 (57)

Выполнил:

Ст. гр. БТК 19-01 ___________ И.Р. Исламов

(подпись, дата)

Проверил:

Доцент, к.т.н. ___________Т.В. Смольникова

(подпись, дата)

Уфа 2021

Исходные данные:



При интерполировании экспериментальных данных выбрать 4-5 равноотстающих точек и построить соответствующий интерполяционный полином:

1. 
   Метод Лагранжа
   

i	1	2	3	4	5
x	34	61	88	115	142
F	355	422	429	446	491

А) Рассмотрим промежуток x∈ [34;88]. Возьмём значение x = 43:

(При n =2)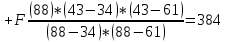




Б) Выбираем точку, значение которой x>88. Например, х = 106:

(При n =2)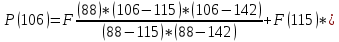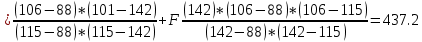





В) Выберем значение в узловой точке, например, при x = 61:
(При n =2)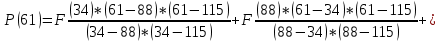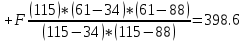

2. 
   Метод Ньютона
   

Для возможности сравнить данный метод с методом Лагранжа, необходимо рассмотреть те же самые значения, что и в предыдущем методе.

i	1	2	3	4	5
x	34	61	88	115	142
F	355	422	429	446	491

1) Необходимо исследовать значение x = 43: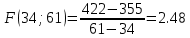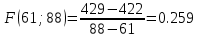







Рассчитаем необходимое нам значение P(x): (для n=2)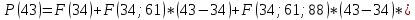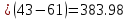





2) Рассмотрим значение при х = 106: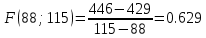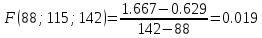







(для n=2)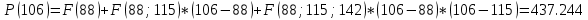



3) Значение при x=61: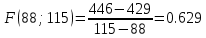







Теперь, рассчитаем необходимое нам значение P(x): (для n=2)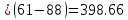

3. 
   Расчет погрешностей.
   

Проведем анализ эффективности каждого метода, сравнив полученные значения с табличными:

1. 
   Метод Лагранжа:
   

2) Метод Ньютона: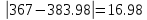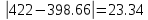







Вывод по ручному расчёту: оба метода имеют одинаковую погрешность, но полученные результаты в обоих методах сильно отличаются от истинных. Причиной тому является резкое изменение значений функции в изначальной таблице, т.е. имевшаяся у нас увеличивающаяся функция в искомых нами точках начинает резко падать и наоборот, поэтому n = 2 в данном случае нам не достаточно.
Программы

1. 
   Метод Лагранжа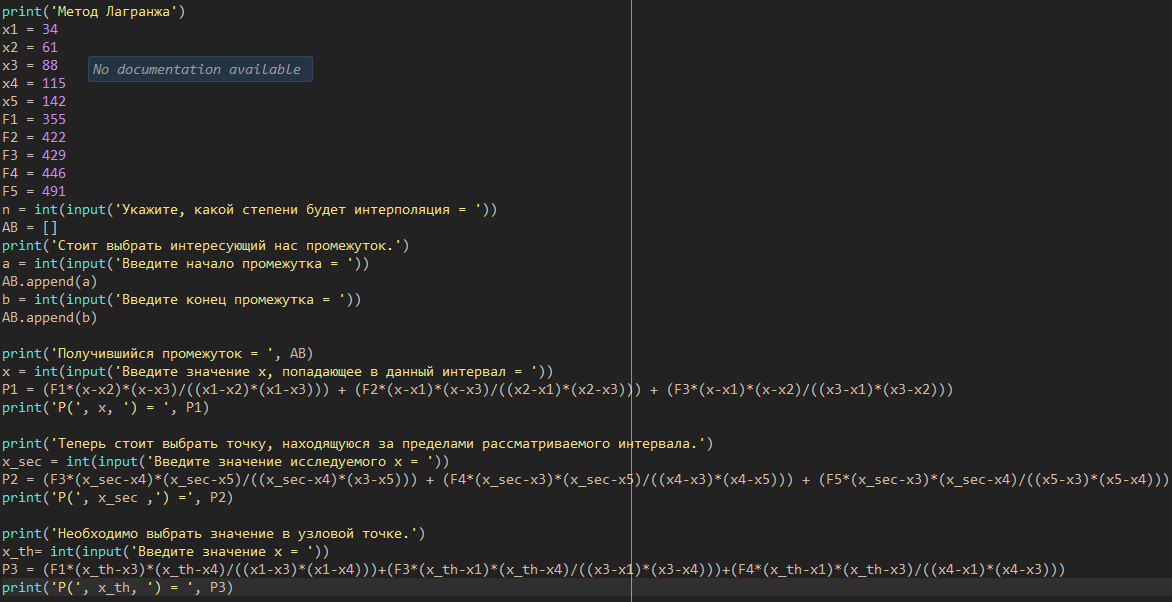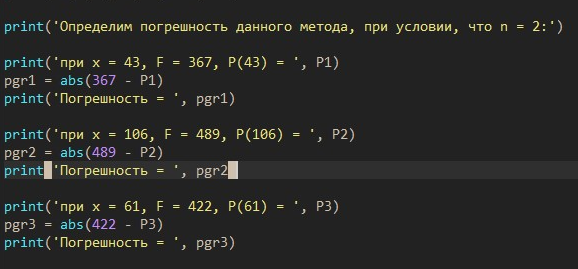
   

Вывод программы метода Лагранжа: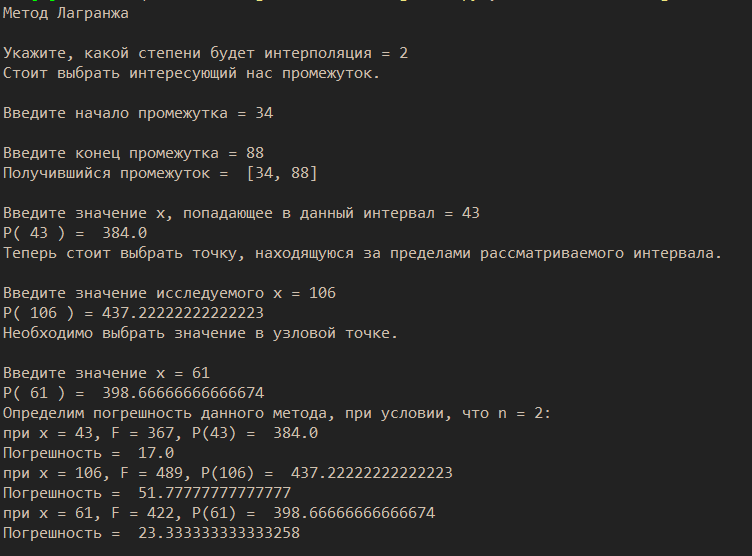

2. 
   Метод Ньютона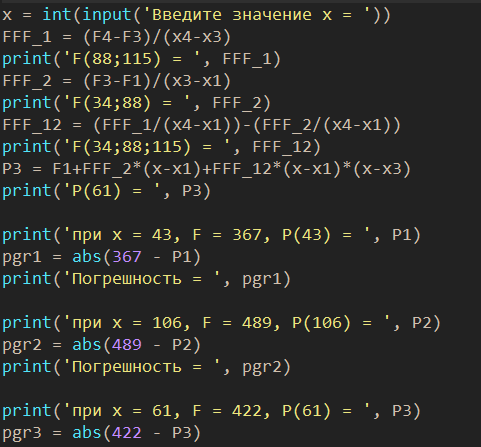
   

Вывод программы метода Ньютона:



Вывод:

В данной работе нами были изучены такие методы, как метод Лагранжа метод Ньютона. Написанные программы выполняют свою функцию, а также подтверждают правильность ручного расчёта. Полученные результаты имеют одинаковую погрешность в обеих программах и совпадают с погрешностями, полученными в ручном расчете Ручной расчёт для данных методов является не совсем эффективным в связи с большей затратой времени. Можно сделать вывод, что точность можно повысить, если увеличить n, но для этого придется использовать большее количество точек для расчетов зависимости f(x)