Лабораторная работа 1 Испытание на растяжение образца из низкоуглеродистой стали Цель испытания
 Скачать 2.33 Mb.
|
|
Лабораторная работа №1 Испытание на растяжение образца из низкоуглеродистой стали Ц  ель испытания:1. Получить диаграмму растяжения и исследовать процесс растяжения испытуемого образца вплоть до его разрушения. 2. Экспериментально подтвердить справедливость закона Гука при растяжении и определить значение модуля упругости Е. 3. Определить механические характеристики материала образца (предел пропорциональности σпр, предел упругости σу., предел текучести σт, пределпрочности Рис.1.1 (временное сопротивление) σпроч., истинное напряжение в месте разрыва образца σразр.ист., условное напряжение в момент разрыва σразр.усл., относительное остаточное удлинение ε и относительное остаточное сужение площади поперечного сечения Ψ (в процентах). 4. Определить марку стали, пользуясь справочной таблицей. 5. Ознакомиться с принципом действия испытательной разрывной машины типа ГМС- 50. Применяемые машины и приборы Разрывная машина. Испытания на растяжение производятся на модернизированной универсальной испытательной машине типа ГМС-50 (гидравлическая машина строительная, максимальная нагрузка - 50 т), которая установлена в лаборатории "Сопротивление материалов (№570) (Рис.1.1). Установка модернизирована, т.е. оснащена дополнительными измерительными устройствами и электронными блоками, позволяющими управлять машиной с помощью ПК: сохранять и обрабатывать результаты эксперимента, выводить информацию на печать, и т.п. Конструкцию и принцип работы установки ГМС-50 можно свести к схеме, изображенной на рис. 1.2: 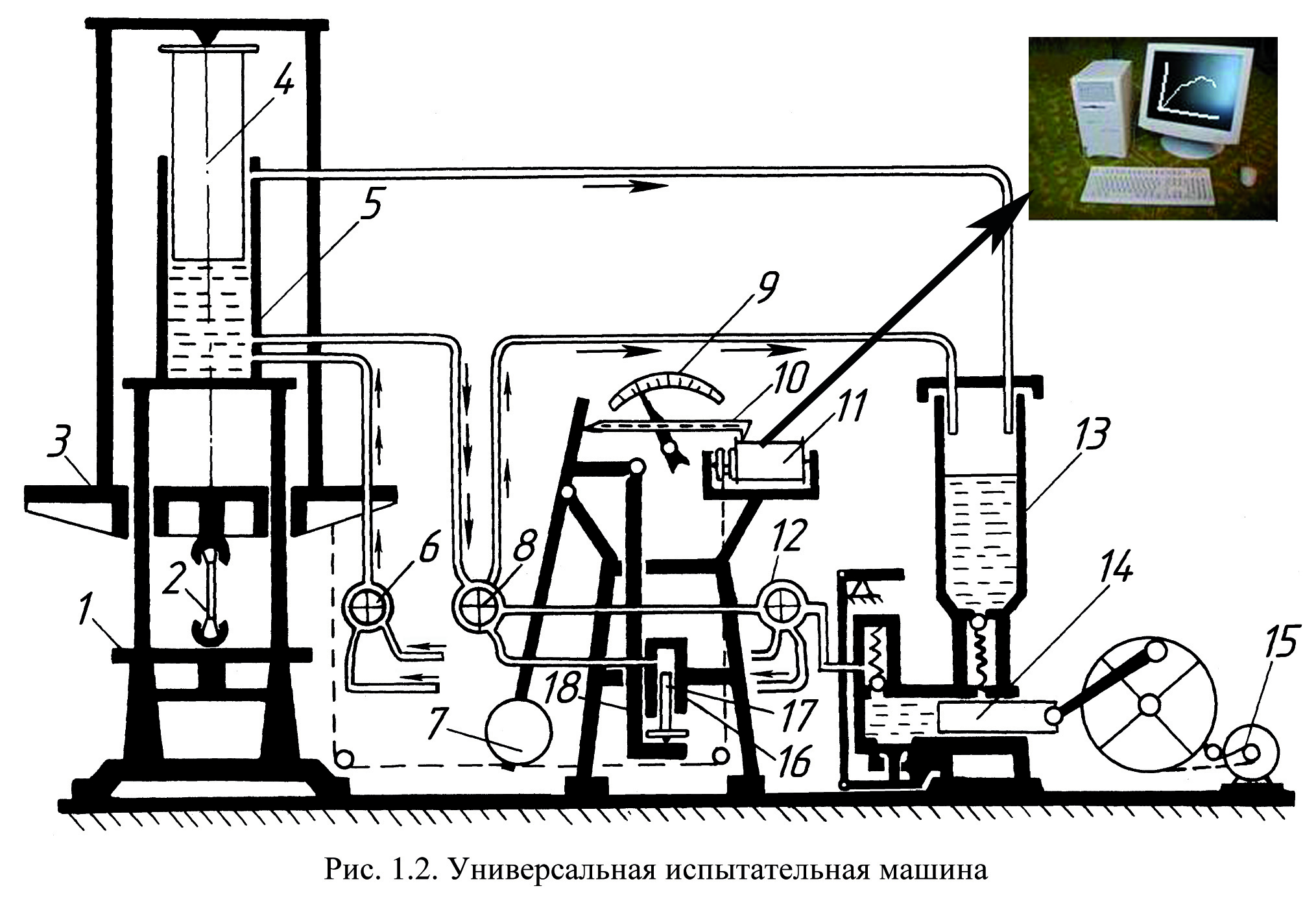 В состав испытательной машины входят: − собственно машина, предназначенная для деформирования образца; − электрогидравлический привод, служащий для создания усилия на испытуемый образец; − маятниковый силоизмеритель, предназначенный для регистрации усилия, производящего деформирование образца. Собственно машина состоит из подвижной 3 и неподвижной 1 траверс. В неподвижной траверсе установлена гидравлическая пара – рабочий цилиндр 5 с поршнем 4. В траверсах укреплены захваты, в которых закрепляется растягиваемый образец 2. Электрогидравлический привод включает плунжерный насос 14 и электродвигатель 15. Насос приводится в действие электродвигателем и масло из резервуара 13 по трубопроводам поступает в рабочий цилиндр 5 машины. Подача масла регулируется рабочим вентилем 12 в зависимости от необходимой скорости нагружения образца. Для более быстрого перемещения траверсы вверх, необходимо для установки ее в надлежащее положение перед испытанием, использовать вентиль 6, для опускания – вентиль 8. Давление масла, поступающего в рабочий цилиндр 5, вызывает перемещение поршня 4, связанного с помощью поперечин и тяг с подвижной траверсой 3. Перемещаясь, траверса будет растягивать или сжимать образец в зависимости от того, где он закреплен (снизу или сверху траверсы). Из рабочего цилиндра 5 давление масла по специальной трубе передается также в цилиндр силоизмерителя 16 и перемещает расположенный в нем поршень 17. Усилие, действующее на поршень цилиндра силоизмерителя, при помощи тяг 18 передается на кривошип маятника 7. Маятник, поворачиваясь на оси, отклоняет угловым рычагом зубчатую рейку 10, связанную с шестеренкой, на оси которой находится стрелка, движущаяся по круговой шкале 9 силоизмерителя. Стрелка в каждый данный момент указывает действующую на образец нагрузку. Маятниковый силоизмеритель представляет собой штангу со сменными грузами 7. Посредством изменения длины маятника и его веса можно изменить максимальное усилие машины. Для рассматриваемых машин возможны установки с максимальным усилием 5, 10, 25 и 50 тонн. В процессе испытания на модернизированной установке текущие значения нагрузки и удлинения образца можно наблюдать на дисплее ПК, где автоматически вычерчивается диаграмма растяжения, которая показывает зависимость между растягивающей силой F, действующей на образец, и вызываемой ею деформацией Δl образца. Установка ГМС -50 в нашей лаборатории модернизирована, т.е. оснащена компьютерной системой, которая включает в себя: 1) датчики измерения параметров испытания: - датчика силы на основе тензометрического датчика давления (точность измерения в диапазоне от 50 до 500кН не хуже +1% ), - датчика линейного перемещения на основе потенциометрического датчика перемещения (предельное разрешение не хуже 0,01 мм), 2) микропроцессорный блок сбора передачи данных от машины ГМС 50 в ПВЭМ. 3) ПЭВМ, принтер, программное обеспечение. Это позволяет: а) регистрировать параметры: нагрузка, перемещение активного захвата в диапазоне рабочего пространства, время, б) производить автоматический расчет механических свойств образца: предела прочности, модуля упругости, предела текучести, предела упругости и др. в) печатать графики: перемещение – нагрузка, деформация - нагрузка, время-нагрузка и др., г) сохранять и редактировать записи в базе данных и.т.п. Измерительные приборы. При выполнении данной работы целесообразно использование таких измерительных приборов, как штангенциркуль (Рис.1.3), рычажный тензометр ТР-294 (Рис.1.5), микрометр (Рис.1.4). Штангенциркуль применяется для измерения расчетной длины образца, его диаметра или толщины и ширины образца, если он плоский. Штангенциркули бывают с нониусами, позволяющими производить отсчеты измерений с точностью до 0,1; 0,05 и 0,02 мм. Выбор инструмента определенной точности производится в зависимости от требований, предъявляемых к данному испытанию. Подробно с устройством и работой со штангенциркулем можно познакомиться в специальной литературе, здесь же приводится только его общий вид (рис. 1.3). М  икрометр позволяет производить обмер диаметра образцов до и после их испытания с более высокой точностью, чем штангенциркулем. Цена деления шкалы микрометра равна 0,01 мм. Однако на глаз можно взять отсчет с точностью до половины деления шкалы, что соответствует 0,005 мм. Общий вид микрометра показан на рис.1.4. Т  ензометр. Для замера линейных деформаций образцов в данной лабораторной работе целесообразно использовать специальные измерительные приборы – механические тензометры рычажного типа. При помощи этих приборов определяют с высокой степенью точности малые деформации образцов, причем показания снимаются визуально. Рабочая схема тензометра рычажного типа показана на рис. 1.5. При работе прибор прижимается к поверхности испытываемого образца при помощи струбцины. Базой прибора является расстояние между ребром призмы 1 и острием ножа 2. Жесткая рамка 6 вместе с призмой 1 составляет часть прибора, воспринимающую деформацию образца. Частью прибора, которая увеличивает деформацию, является рычаг 3, жестко соединенный с призмой 1, и стрелка 5, шарнирно соединенная с рычагом тягой 4. Для повышения точности отсчетов шкала 7 снабжена прорезью с зеркалом. При увеличении длины l (базы тензометра l = Б) на величину Δl происходит поворот призмы вокруг ее верхнего ребра на некоторый угол. Вместе с призмой на тот же угол повернется рычаг 3, который при помощи тяги отклонит стрелку 5. Вследствие поворота стрелки нижний ее конец переместится по шкале на величину ΔВ с отсчета В1 на отсчет В2. Коэффициент увеличения k зависит от соотношения плеч рычагов 3 и 5 и равен k = ΔВ/Δl. В нашей работе используются тензометры рычажного типа с коэффициентом увеличения 1000 и с базой Б= l = 20 мм (в работе обозначается l = S = 20 мм). Цена деления тензометра- 0,001мм. О 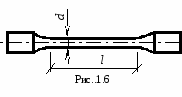 бразцы для испытаний на растяжение чаще всего делают цилиндрической или плоской формы с головками на концах для закрепления их в захватах машины (рис. 1.6). Наиболее распространены цилиндрические образцы, у которых расчетная длина l = 5d (короткие, пятикратные образцы) и l = 10d (длинные, десятикратные образцы).Формы и размеры головок и переходных частей цилиндрических и плоских образцов определяются способом крепления образцов в захватах испытательной машины. Способ крепления должен предупреждать проскальзывание образцов в захватах, смятие опорных поверхностей, деформацию головок и разрушение образца в местах перехода от рабочей части к головкам и в головках. Перед установкой образца в испытательную машину производится измерение диаметра и длины его рабочей части. Диаметр рабочей части измеряется по двум взаимно перпендикулярным направлениям в трех сечениях. Точность измерения диаметра 0,1 мм. Затем образец устанавливается в захваты испытательной машины. После проверки готовности машины к испытанию ее включают и растягивают образец согласно программе испытания до его разрушения. Теоретические положения Диаграмма растяжения В процессе испытания ведется наблюдение за поведением образца, за диаграммой на мониторе компьютера, и за показаниями стрелки силоизмерителя машины. Типичный вид диаграммы растяжения малоуглеродистой стали - зависимость между растягивающей силой F, действующей на образец, и вызываемой ею деформацией образца Δl изображен на рис. 1.7. 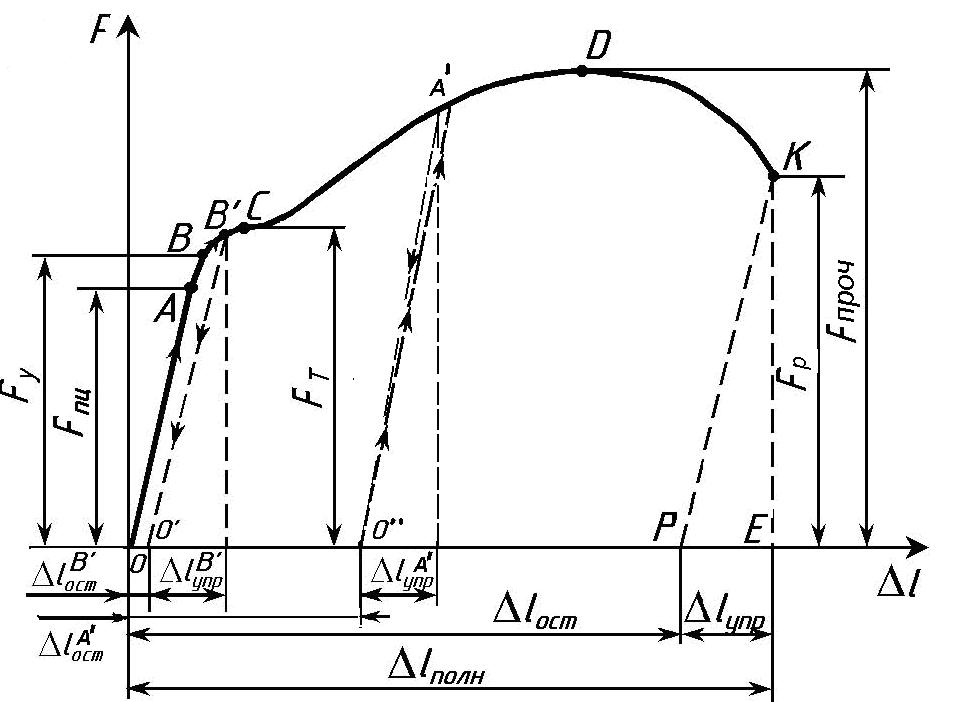 Рис.1.7. Диаграмма растяжения образца из малоуглеродистой стали - Ст3. (F - растягивающая сила, Δl = lконечная длина –lначальная - абсолютное удлинение образца). Рассмотрим характерные участки и точки этой диаграммы, а также соответствующие им стадии деформирования образца. От начала нагружения до определенного значения растягивающей силы F пц (точка А) имеет место прямая пропорциональная зависимость между силой F и удлинением Δl (участок ОА): Fпц = k Δl . Эта пропорциональность впервые была замечена в 1670 г. Робертом Гуком и получила в дальнейшем название Закона Гука. Величина силы F пц , до которой остается справедливым закон Гука, зависит от размеров образца и физических свойств материала. Напряжение, вызванное этой силой, называется пределом пропорциональности и вычисляется по формуле: σ пц = Fпц /A, где А - площадь поперечного сечения образца. Таким образом, пределом пропорциональности называется напряжение, после которого нарушается закон Гука. Известно, что деформация называется упругой, если она полностью исчезает после разгрузки. Допустим, что, постепенно повышая нагрузку F, будем при каждом ее значении производить полную разгрузку образца. Пока сила F не достигнет определенной величины F y (точка B), вызванные нею деформации будут полностью исчезать при разгрузке. Процесс разгружения при этом будет изображаться той же линией, что и линия нагружения. Участок диаграммы ОВ соответствует упругой стадии растяжения образца и называется участком упругости. Наибольшее напряжение, до которого остаточная деформация при разгрузке не обнаруживается, называется пределом упругости. Это напряжение вызывается силой F y и определяется по формуле : σ у = Fy/A . Предел упругости является характеристикой, не связанной с законом Гука. Точка В может располагаться как выше, так и ниже точки А. Эти точки, а следовательно, и значения напряжений σ пц и σ у близки друг другу и обычно различием между ними пренебрегают. В случае, если растягивающее усилие выше Fy (точка B′) , при разгрузке образца деформации полностью не исчезают и на диаграмме линия разгрузки будет представлять собой прямую B′О′, уже не совпадающую с линией нагружения, а параллельную ей. В этом случае деформация образца состоит из упругой Δl упр и пластической (остаточной) Δl ост деформации. Выше точки В при дальнейшем растяжении образца кривая растяжения становится криволинейной и плавно поднимается до точки С, где наблюдается переход к горизонтальному участку, называемому участком текучести. На этой стадии растяжения удлинение образца растет при постоянном значении растягивающей силы F т. Такой процесс деформации называется текучестью материала и сопровождается остаточным (пластическим) удлинением, не исчезающим после разгрузки. Пределом текучести σ т называется наименьшее напряжение, при котором деформация образца происходит при постоянном растягивающем усилии F т , и вычисляемое по формуле: σ т = Fт /A Начало пластической деформации соответствует наступлению некоторого критического состояния металла, которое может быть обнаружено не только по остаточным деформациям, но и по ряду других признаков. При пластической деформации повышается температура образца, у стали изменяются электропроводность и магнитные свойства. В процессе текучести на отшлифованной поверхности образца можно наблюдать появление линий (полос скольжения), наклоненных примерно под углом 450 к оси образца (рис.1.8, а). Эти линии являются следами взаимных сдвигов кристаллов, вызванных касательными напряжениями. 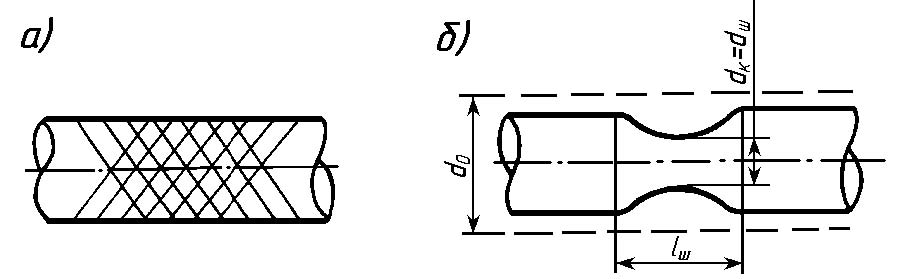 Рис.1.8 Линии сдвига называются линиями Чернова по имени знаменитого русского металлурга Д. К. Чернова (1839 – 1921), впервые обнаружившего их. Удлинившись на некоторую величину при постоянном значении силы, т.е. претерпев состояние текучести, материал снова приобретает способность сопротивляться растяжению (упрочняться). Этот участок диаграммы С Д называется участком упрочнения (рис.1.7) . В точке D усилие достигает максимального значенияF проч . Наличие участка упрочнения (от конца площадки текучести до наивысшей точки диаграммы растяжения) объясняется микроструктурными изменениями материала: когда нагрузка на образец возрастает, микроскопические дефекты (линейные и точечные) группируются так, что развитие сдвигов кристаллов, вызванных касательными напряжениями, затрудняется, а потому сопротивление материала сдвигу начинает возрастать и приближаться к его сопротивлению отрыву. Если процесс растяжения остановить в пределах участка С Д, например, в точке А", и начать разгружать образец, то деформация его будет исчезать пропорционально снимаемой нагрузке, т. е. по прямой А"О"", параллельной прямой АО. При повторной нагрузке этого образца линия нагрузки совпадет с прямой А"О"", т.е. увеличится участок пропорциональности. При дальнейшем увеличении растягивающей силы кривая диаграммы совпадет с кривой A" CK. Часть диаграммы, расположенная левее линии А"О"", окажется отсеченной. т.е. начало координат переместится в точку О"" (Рис.1.7, Рис.1.8.а). Остаточное удлинение после разрыва будет меньше, чем в образце, не подвергавшемся предварительной пластической деформации. Таким образом, предварительная вытяжка образца за предел текучести изменяет некоторые механические свойства стали - повышает ее предел пропорциональности, т.е. делает ее более упругой, и уменьшает остаточное удлинение, т.е. делает ее более хрупкой (Рис.1.8.а). 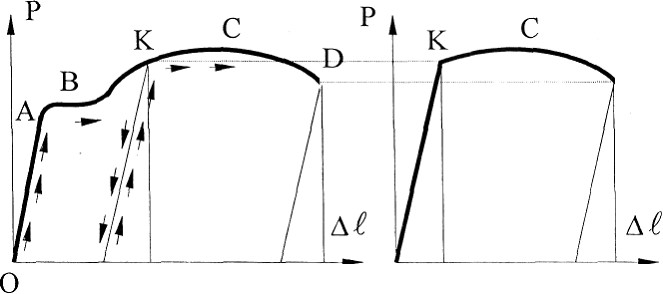 Рис.1.8.а. Диаграммы растяжения: слева - полная для предварительно незагруженного образца, справа-укороченная для предварительно загруженного до точки. К образца Изменение свойств материала в результате деформации за пределом текучести называется наклепом. После операции наклепа модуль упругости Е возрастает на 20-30 %. При достижении усилияF проч (точка D) на образце появляется местное сужение, так называемая шейка (Рис. 1.8, б). Под действием силы далее быстро уменьшается площадь ее сечения, что вызывает падение нагрузки, и в момент, соответствующий точке K диаграммы и силе Fк, происходит разрыв образца по наименьшему сечению образца - в шейке. До точки D диаграммы, соответствующей F проч., каждая единица длины образца удлинилась примерно одинаково; точно так же во всех сечениях одинаково уменьшались поперечные размеры образца. С 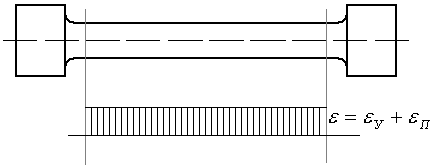 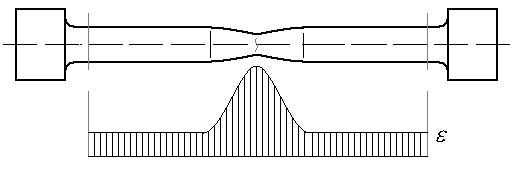 момента образования шейки вся деформация образца локализуется на малой длине ( l ш ≈ 2d0 ) в области шейки, а остальная часть образца практически не деформируется: Рис 1.8,б Диаграмма условных напряжений. Механические характеристики материалов. Координаты диаграммы растяжения F −Δl (рис.1.7) не являются качественными характеристиками материала, т. к. растягивающая образец сила F зависит от площади сечения, а удлинение образца Δl – от его длины. Чтобы исключить влияние размеров образца и получить диаграмму, характеризующую поведение не образца, а самого материала, диаграмму растяжения перестраивают в координатах σ −ε (напряжение - относительное удлинение) путем деления ординат F на первоначальную площадь сечения образца A 0, а абсцисс Δl на первоначальную длину образца l . Это равносильно изменению масштабов по обеим осям. Перестроенная таким образом диаграмма называется диаграммой условных напряжений (рис.1.9). 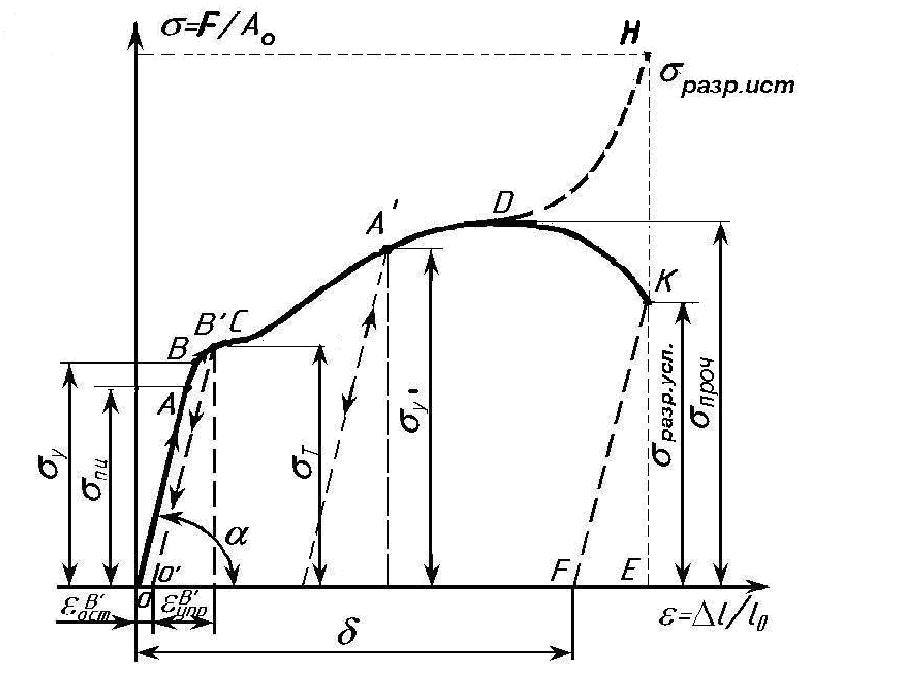 Рис. 1.9. Диаграмма условных напряжений. Название диаграмма условных напряжений объясняется тем, что площадь образца в процессе испытания в действительности изменяется. До образования шейки (точка D) эти изменения незначительны, а вот на участке DK (Рис.1.9) с образованием шейки действительная площадь поперечного сечения образца и первоначальная площадь А о , по которой определяются ординаты диаграммы, значительно отличаются друг от друга. Деля величину силы на действительную площадь поперечного сечения образца А, можно получить значения истинных напряжений и построить кривую истинных напряжений диаграммы DH. Таким образом, на рис.1.9 участок DK - условная диаграмма, а участок DH - истинная диаграмма напряжений образца. Прямолинейный участок диаграммы ОА соответствует участку упругости образца. Закон Гука в данных координатах имеет вид:
Из диаграммы напряжений σ- ε видно, что tg α = σ / ε = E , т.е. модуль упругости (Модуль Юнга) при растяжении равен тангенсу угла наклона прямолинейного участка диаграммы к оси абсцисс. Относительное удлинение образца: ε = Δl / l ∙ 100 % , относительное сужение образца: Ψ = ΔА /А l ∙ 100 % после разрыва являются характеристиками пластичности материала. В зависимости от величины этого удлинения материалы делят на пластичные, у которых ε > 5% и хрупкие, у которых ε < 5%. Соответственно, чем больше относительное сужение, тем пластичней материал. К пластичным материалам относится малоуглеродистая сталь, медь, свинец, и др., к хрупким - закаленная сталь, чугун, стекло, камень, бетон и др. Сравнивая рис. 1.7 и рис. 1.9, видим, что ординатам характерных точек диаграммы растяжения F (Fпц, Fпц А", Fy, Fт, F проч, Fразр) соответствуют следующие механические характеристики материала образца: – предел пропорциональности σпц= Fпц /A – предел упругости σу = Fy/A – предел пропорциональности при повторной нагрузке (наклеп) σy" = Fпц А" /A – предел текучести σт = Fт /A – временное сопротивление растяжению (предел прочности при растяжении) σ проч = Fпроч /A – истинное напряжение в момент разрыва (Aш – площадь поперечного сечения шейки) σ разр. ист = Fpазр /A ш – условное напряжение в момент разрыва (не учитывается диаметр шейки!!!) σ разр. усл = Fpазр /A –абсолютное остаточное удлинение образца Δl = lкон - lнач – относительное остаточное удлинение образца ε = 100Δl / l % – абсолютное остаточное сужение площади поперечного сечения ΔА = А – Аш – относительное остаточное сужение площади поперечного сечения Ψ = 100ΔА /А %. З 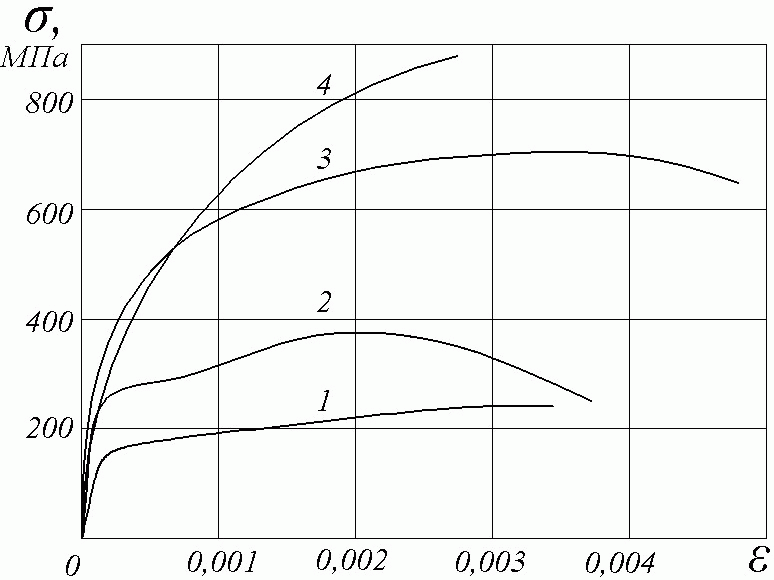 аметим, что площадка текучести есть у сравнительно немногих металлов - малоуглеродистой стали, латуни и некоторых оттоженных марганцовистых и алюминиевых бронз. Большинству же металлов свойственен постепенный переход в пластическую область. Для сравнения на рис. 2а изображены диаграммы растяжения нескольких металлов: кривая 1- бронзы, 2 - углеродистой стали, 3 - никелевой стали , Рис.2,а 4-марганцовистой стали. Р 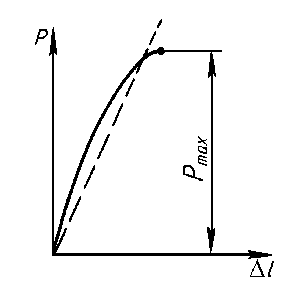 азрыв образцов из хрупких материалов происходит при весьма незначительном удлинении и без образования шейки. При испытании на растяжение хрупких материалов определяют обычно только максимальную нагрузку. На рис. 2, б приведена диаграмма Рис.2,б растяжения хрупкого материала - серого чугуна. Порядок выполнения работы
Пример обработки опытных данных Лабораторная работа № 1. Испытание на растяжение образца из низкоуглеродистой стали Цель испытания: 1. Получить диаграмму растяжения и исследовать процесс растяжения образца из малоуглеродистой стали вплоть до его разрушения. 2, Экспериментально подтвердить справедливость закона Гука при растяжении и определить значение модуля упругости Е. 3. Определить механические характеристики материала образца (предел пропорциональности σ пр., предел упругости σ упр., предел текучести σ тек., временное сопротивление (предел прочности) σ проч., истинное напряжение в месте разрыва образца σ разр.ист., условное напряжение в момент разрыва σ разр.усл.., относительное остаточное удлинения εи относительного остаточного сужения площади поперечного сеченияΨ(в %). 4. Определить марку стали, пользуясь справочной таблицей. Машины и материалы: Испытательная разрывная машина ГМС - 50, тензометр, штангенциркуль, образец из низкоуглеродистой стали. Схема ГМС-50: 1 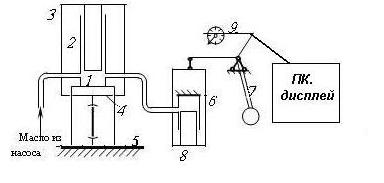 -рабочий цилиндр, 2-поршень, 3- тяги, связанные с верхним захватом образца 4, 5- неподвижная станина, соединенная с нижним захватом образца. 6 - измерительный цилиндр, 7- маятник, 9 стрелочный механизм, ПК, дисплей.Схемы образца: До разрыва: После разрыва:   Схема крепления рычажного тензометра на образце: 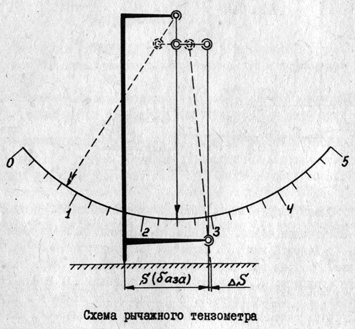  Таблица наблюдений:
Результаты испытания: Данные размеров образца до опыта и после опыта заносим в базу данных Программы испытания образцов. По полученным с помощью ПЭВМ диаграмме растяжения образца - зависимости F-∆ l (Рис.1.) и диаграмме напряжений (σ - ε ) ( (Рис.2) определяем механические и пластические характеристики материала. Рис.1.Диаграмма растяжения Рис.2.Диаграмма напряжений 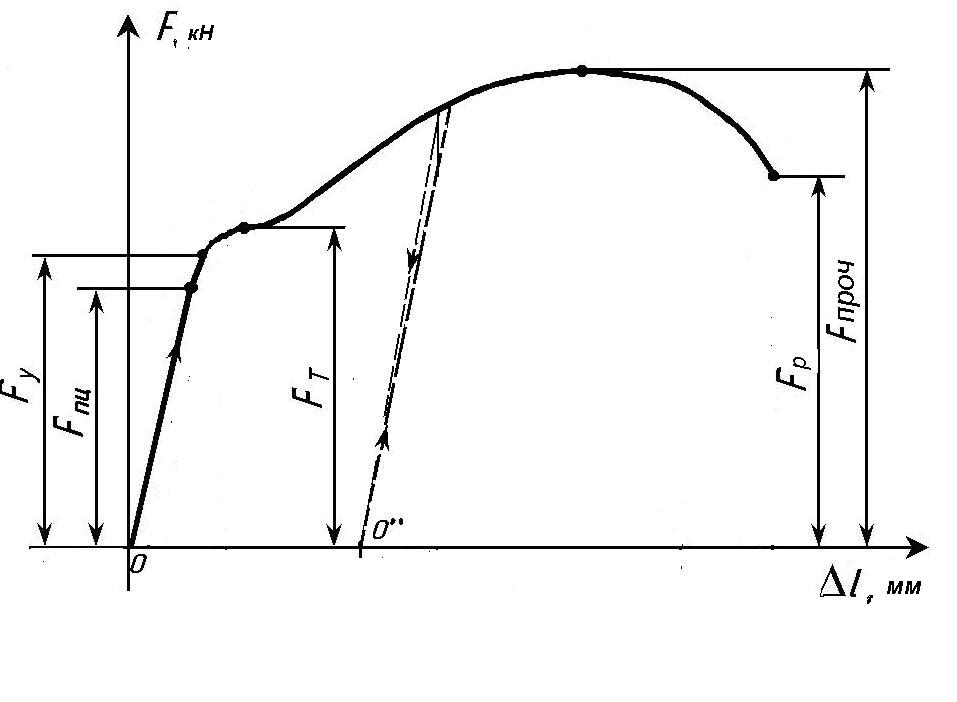 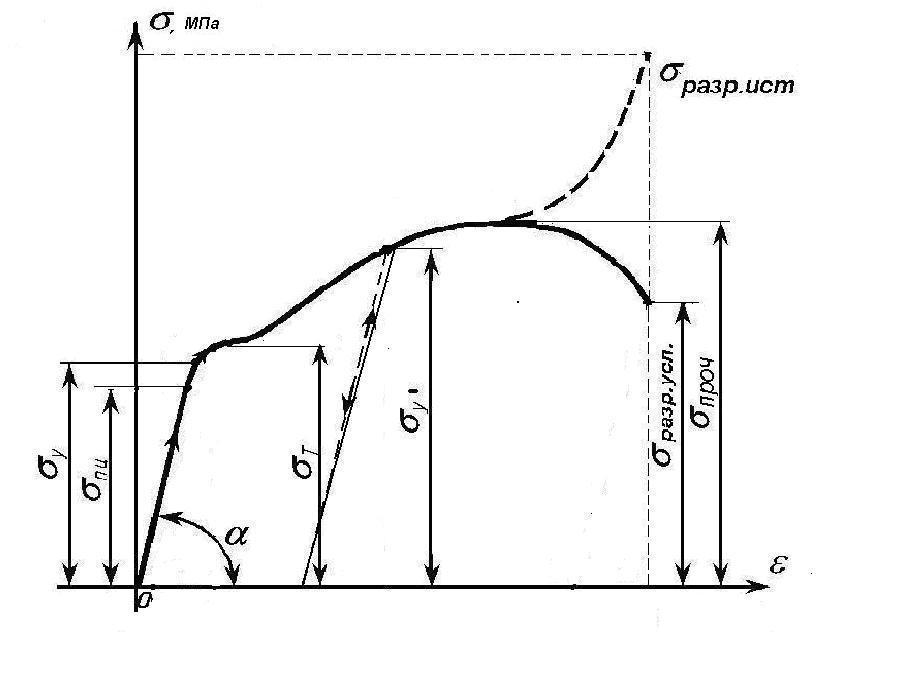 – предел пропорциональности σпц= Fпц /A= – предел упругости σу = Fy/A= – предел пропорциональности при повторной нагрузке (наклеп) σy" = Fпц А" /A= – предел текучести σт = Fт /A= – временное сопротивление растяжению (предел прочности при растяжении) σ проч = Fпроч /A= – истинное напряжение в момент разрыва (Aш – площадь поперечного сечения шейки) σ разр. ист = Fpазр /A ш= – условное напряжение в момент разрыва (не учитывается диаметр шейки!!!) σ разр. усл = Fpазр /A= –абсолютное остаточное удлинение образца Δl = lкон - lнач= – относительное остаточное удлинение образца ε = 100Δl / l % = – абсолютное остаточное сужение площади поперечного сечения ΔА = А – Аш = – относительное остаточное сужение площади поперечного сечения Ψ = 100ΔА /А %.= Определение модуля упругости материала Е - модуля Юнга: Б=S - база тензометра равна 2см. Цена деления тензометра: 1 деление = 10-3 мм
Среднее упругое удлинение образца при нагрузке ΔF: ΔSср = ............ (см) Модуль упругости Е = σ / ε =  = ............. (кг/см2, МПа)Сравнивая полученные механические характеристики образца с табличными данными в учебнике и в Таблице 1, определяем марку стали образца: Материал образца - ....
Примечание. В знаменателе указана соответствующая характеристика при сжатии. Контрольные вопросы.
прочности, пластичности, упругости, жесткости.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||