Лабораторная работа 1 исследование косого удара о наклонную плоскость выполнил студент гр. Ф. И. О
 Скачать 104.5 Kb.
|
|
ЛАБОРАТОРНАЯ РАБОТА №1 ИССЛЕДОВАНИЕ КОСОГО УДАРА О НАКЛОННУЮ ПЛОСКОСТЬ Выполнил студент гр. _____________ Ф.И.О _________________ Проверил ________________________ дата ___________________ Цель работы: рассмотреть кинематику движения шара после удара о плоскость; определить коэффициент восстановления скорости шара. Порядок выполнения работы 1. Перемещением муфты А установить произвольный наклон плоскости (примерно 10-15°). Измерить высоты H1 и H2, длину наклонной плоскости l между линиями L1 и L2 (см.рис. 1) и определить  .Примечание. Можно произвольно изменять длину наклонной плоскости  , изменяя при этом другие высоты H1 и H2.2. Перемещением муфты B установить произвольную высоту h (17 – 20 cм) бункера C над наклонной плоскостью. Отцентрировать установку бункера так, чтобы шарик после отскока ударился еще один раз о наклонную плоскость в направлении ее продольной оси. 3. Положить на наклонную плоскость узкую полоску бумаги краем вдоль черты L1, накрыть сверху копировальной бумагой и закрепить оба листа скобой. При проведении эксперимента скобу не трогать. 4. Поместить шарик в бункер C в слегка открытое отверстие (это позволит более точно фиксировать начальное положение шарика). Затем медленно открыть заслонку, дав шарику провалиться. Ударившись о плоскость, шарик отскочит и оставит след на бумаге. 5. Обозначить точку удара на бумаге точкой 1. Отогнуть от линии L1 и полоску бумаги и копировальную бумагу таким образом, чтобы повторное падение шарика из бункера пришлось на металлическую поверхность; отскочив от нее, шарик второй раз ударится о поверхность и оставит след на бумаге. Эту точку обозначить цифрой 1’. 6. Повторить опыт при отогнутой бумаге 9 раз, обозначая следы от повторных ударов соответственно 1’, 2’, ..., 3’. 7. Снять листы с плоскости, определить расстояние xi между точками 1-1’, 1-2’, 1-3’, ..., 1-9’ и занести в табл.1. 8. Вычислить среднее значение  .9. Определить случайные отклонения ∆xi = xi – < x > каждого измерения расстояния, среднее квадратичное отклонение  . Вычислить погрешность ∆x результата измерений:  (n-количество точек).10. Вычислить среднее значение коэффициента восстановления скорости по формуле 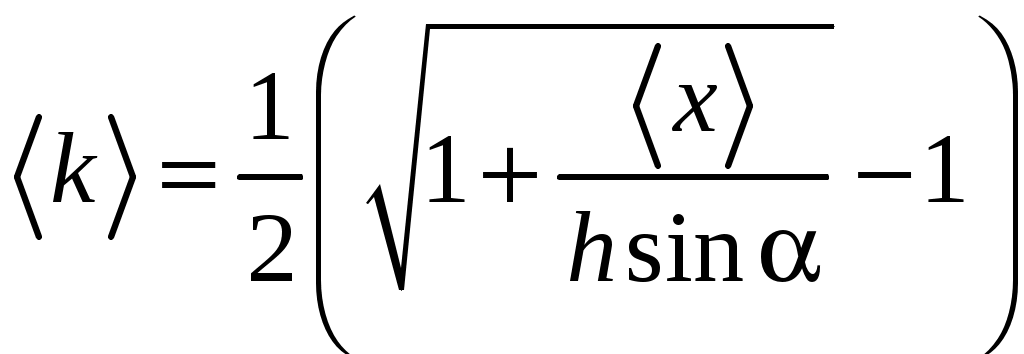 . 11. Вычислить абсолютную ∆k и относительную E погрешности: 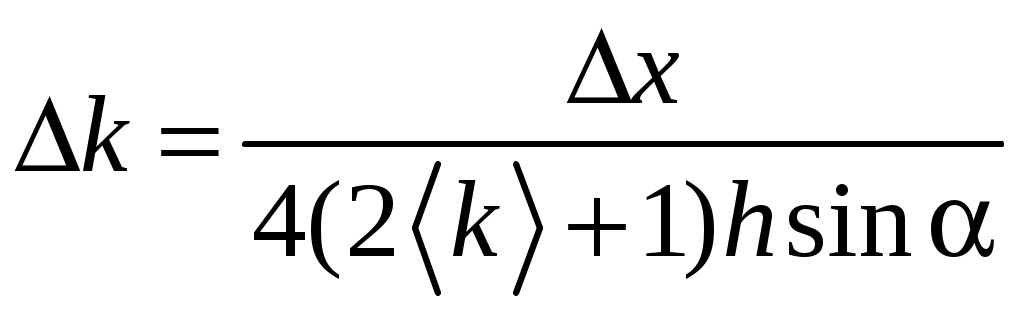 ;  .12. Результаты измерений и расчетов записать в табл.1 и 2. 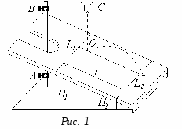 Таблица 1
Таблица 2
13. Записать результат в виде:  = ....... ± ....... В реальных случаях 0 < kc < 1. Контрольные вопросы 1. Что такое коэффициент восстановления скорости, какова методика его определения в данной работе? 2. Записать закон движения шарика между первым и вторым соударениями с наклонной плоскостью координатным способом. Как определить расстояние x и время t между этими соударениями?  3. Сформулировать закон сохранения полной механической энергии. Как он применяется в данной работе?4. Радиус-вектор частицы изменяется во времени по закону  . В момент времени t = 1 с частица оказалась в некоторой точке А. Выберите правильное направление скорости частицы в этот момент времени. а) 1; б) 2; в) 3; г) 4; д) на рисунке нет правильного направления  5. Камень бросили под углом к горизонту со скоростью V0. Его траектория в однородном поле тяжести изображена на рисунке. Сопротивления воздуха нет. Модуль тангенциального ускорения  на участке А-В-С:1) уменьшается 2) увеличивается 3) не изменяется 6. Прямолинейное движение точки описывается уравнением  (в единицах СИ). Средняя скорость точки за время движения до остановки в м/с равна ....Литература Савельев И.В. Курс общей физики. т.1. М:Наука, 1986.- гл.III, §19, 24, 25, 27 |