Лабораторная работа 1 Исследование линейной резистивной цепи постоянного тока Теоретическая часть Электрической цепью
 Скачать 132.21 Kb. Скачать 132.21 Kb.
|
|
Лабораторная работа №1 Исследование линейной резистивной цепи постоянного тока Теоретическая часть Электрической цепьюназывают совокупность соединенных друг с другом элементов, по которым может протекать электрический ток [1,7,11]. Для протекания тока необходимы источники электрической энергии – источники напряжения (ЭДС) или тока. Электрическая цепь содержит также устройства, в которых энергия электрического тока преобразуется в другие виды энергии (механическую, тепловую, световую и т.д.). Эти устройства называются нагрузками. Для замыкания и размыкания цепей используют выключатели того или иного вида. Электрический ток есть направленное (упорядоченное) движение носителей зарядов. В проводниках носителями отрицательных зарядов являются электроны, в жидкостях (электролитах) носители положительных и отрицательных зарядов – ионы. В полупроводниках носителями отрицательных зарядов являются электроны, носителями положительных зарядов – дырки. Дыркойназвали вакантное место в атоме полупроводника, незанятое электроном. Ток, неизменный во времени, называют постоянным. Он обозначается символом I. Количественно ток равен заряду q, который пересекает сечение проводника за единицу времени t (1 секунду) I = q / t. Для поддержания электрического тока требуется обеспечивать разделение носителей отрицательных и положительных зарядов, что и происходит в источниках электрической энергии. Способность источника совершать работу по разделению зарядов характеризуется электродвижущей силой (ЭДС), которая обозначается символом Е. Когда источник подключен к цепи, возникает направленное движение зарядов под действием сил притяжения разноименных и отталкивания одноименных зарядов, т.е. электрический ток. Вне источника положительные носители заряда движутся от его положительного зажима (полюса) к отрицательному зажиму (полюсу). Направление движения отрицательных зарядов противоположно движению положительных зарядов. Работа, совершаемая при движении зарядов по элементам электрической цепи характеризуется напряжением, которое обозначаетcя символом U. Напряжение и ток на участке цепи постоянного тока связаны законом Ома I = U/RилиU = RI, где R – коэффициент пропорциональности между током и напряжением, называемый сопротивлением. Мощность преобразования электрической энергии в другие виды энергии выражается через ток и напряжение (закон Джоуля-Ленца) [7, 8, 18] P = UI = RI2 = U2/R. Изображение электрической цепи с помощью условных обозначений называют схемой электрической цепи (рисунок 2.1). 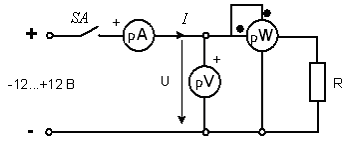 Рисунок 2.1 – Схема электрической цепи На расчётных схемах (т.е. на схемах, предназначенных для расчёта электрической цепи) показывают стрелками направления токов и напряжений. За направление тока принимают направление движения положительных зарядов, а за направление напряжения – направление от положительного полюса источника к отрицательному. Когда истинные направления неизвестны, на схеме показывают условные (или предполагаемые) положительные направления. Цепь постоянного тока с последовательным соединением резисторовЕсли резисторы или любые другие нагрузки соединены последовательно (рисунок 2.2), по ним протекает один и тот же ток. Величина тока определяется приложенным напряжением U и эквивалентным сопротивлением Rэкв I = U / Rэкв, где Rэкв = R = R1 + R2 + R3. 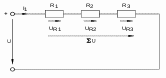 Рисунок 2.2 – Последовательное соединение резисторов На каждый отдельный резистор при этом приходится некоторое частичное падение напряжения. Сумма частичных падений напряжений, в соответствии со вторым законом Кирхгофа, равна полному приложенному напряжению IR1 + IR2 + IR3 = U. Цепь постоянного тока с параллельным соединением резисторовЕсли резисторы или любые другие нагрузки соединены параллельно (рисунок 2.3), все они находятся под одинаковым напряжением U = UR1 = UR2 = UR3 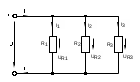 Рисунок 2.3 – Параллельное соединение резисторов В каждой ветви цепи протекает свой ток. Сумма токов всех ветвей в соответствии с первым законом Кирхгофа равна полному току I = I1 + I2 + I3. Величина тока ветви зависит от приложенного напряжения и сопротивления данной ветви 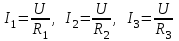 . .Ток в неразветвленной части цепи зависит от приложенного напряжения и эквивалентного сопротивления цепи 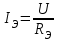 . .Для вычисления эквивалентного сопротивления цепи служит формула 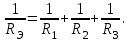 , ,для цепи с двумя параллельно соединенными резисторами формула для расчета RЭ приобретает вид 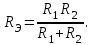 Цепь постоянного тока при смешанном соединении резисторовНа рисунке 2.4 показан пример цепи со смешанным (т.е. последовательно-параллельным) соединением резисторов. Цепь состоит из последовательно (R1 и R2) и параллельно (R3 и R4) соединенных резисторов. 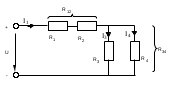 Рисунок 2.4 – Смешанное соединение резисторов Участки цепи с последовательным и параллельным соединением резисторов относительно друг друга соединены последовательно. Чтобы вычислить полное сопротивление цепи сначала определяют эквивалентное сопротивление параллельного участка 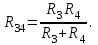 Затем определяют эквивалентное сопротивление всей цепи, состоящей теперь из трёх последовательно соединённых сопротивлений 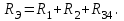 Для расчёта токов в этой цепи необходимо сначала определить по закону Ома ток в эквивалентном сопротивлении, он же в сопротивлениях R1 и R2 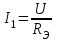 . .После этого, опять же по закону Ома, определяются напряжение на участке с параллельным соединением и токи в параллельных ветвях 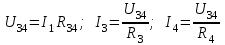 . .Практическая часть Цель работы. Изучить методы экспериментального исследования распределения токов в разветвлённой электрической цепи с резисторами при воздействии нескольких источников напряжения постоянного тока. Получить экспериментальное подтверждение Законов электрических цепей и методов их расчёта. Приборы и оборудование. Исследуемая электрическая цепь собирается из элементов, располагаемых на панели стенда. К элементам относятся резисторы, находящиеся на отдельных панелях выданных преподавателем, и два источника напряжения постоянного тока, клеммы которых находятся непосредственно на стенде. Источники питания посредством переключателей (тумблеров) могут устраняться из электрической цепи. Величины сопротивления резисторов, напряжения на элементах электрической цепи и потенциалы точек электрической цепи замеряются цифровым мультиметром. При измерении тока мультиметром располагайте на наборном поле красный провод слева, чёрный справа (соответственно цвету клемм на мультиметрах). Значение токов записываются со знаком, указанным на цифровом табло мультиметра. Рабочее задание. Измеритьцифровым мультиметром величины сопротивлений резисторов, используемых в качестве элементов электрической цепи, и напряжения на разомкнутых зажимах (клеммах) источников напряжения. Результаты измерений занести в таблицу 2.1. Таблица 2.1 – Результаты измерений
2. Собрать электрическую цепь по схеме (рисунок 2.5). 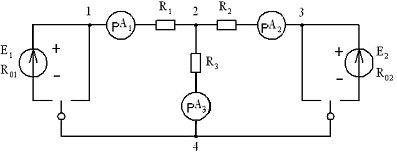 Рисунок 2.5 – Исследуемая схема Подключить к цепи оба источника Е1 иЕ2 . Измерить токи I1, I2 и I3 (протекающие через резисторы R1, R2, R3) и напряжения на источниках U14, U34. Используя пункт лабораторной работы «Методические указания» вычислите по результатам измерений внутренние сопротивления источников R01и R02. Результаты эксперимента занесите в таблицу 2.2. Таблица 2.2 – Результаты эксперимента
Проверьте результаты проведённого эксперимента используя уравнения первого и второго законов Кирхгофа. Расчёты запишите в отчёт. 3. Приняв за базисную точку – точку 4, считая, что потенциал 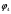 равен нулю, измерить потенциалы всех остальных пронумерованных на схеме точек. Результаты измерений занести в таблицу 2.3. равен нулю, измерить потенциалы всех остальных пронумерованных на схеме точек. Результаты измерений занести в таблицу 2.3.Таблица 2.3 – Результаты эксперимента
Проверьте результаты проведённого эксперимента, определив потенциалы узловпо известным значениям токов и эдс (таблица 2.2), используя пункт лабораторной работы «Методические указания». 4. Для внешнего контура схемы (рисунок 2.5), используя результаты таблицы 2.3, постройте потенциальную диаграмму [2-5]. 5. Исключая из схемы (рисунок 2.5) посредством тумблеров поочерёдно источники Е1 иЕ2,измерьте токи через резисторы R1, R2, R3, обратите внимание на направления токов. Определите токи I1, I2, I3 при действии в цепи обоих источников питания, используя принцип суперпозиции (метод наложения). Результаты опыта занесите в таблицу 2.4. 6. Используя метод эквивалентного двухполюсника, определите ток в ветви «2-3». Для этого определите опытным путём параметры эквивалентного активного двухполюсника (т.е. Uхх ветви 2-3; и Rвн относительно ветви 2-3), используя пункт лабораторной работы «Методические указания». Таблица 2.4 – Результаты эксперимента
Методические указания К опыту 2:Внутреннее сопротивление источника напряжения при известной величине его ЭДС (Е) может быть определено по величине напряжения на его зажимах U при каком-либо значении потребляемого тока 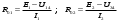 К опыту 3: 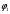 = =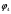 + Е1; + Е1;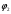 = =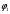 –I1R1; –I1R1;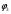 = =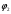 –I2R2; –I2R2;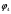 = =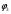 –Е2 =0. –Е2 =0.К опыту 4: Для построения потенциальной диаграммы используйте уравнения предыдущего пункта «Методических указаний». По оси абсцисс откладываются значения сопротивлений участков цепи, по оси ординат – значения потенциалов узлов. Общий вид потенциальной диаграммы представлен на рисунке 2.6.  Рисунок 2.6 – Общий вид потенциальной диаграммы К опыту 6: Ток по методу эквивалентного двухполюсника в выделенной ветви электрической цепи (рисунок 2.6) определяется выражением 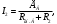 где ЕА – ЭДС эквивалентного двухполюсника (ЕА=Uхх), определяется путём измерения напряжения на разомкнутых зажимах ветви; Rвн.А – внутреннее сопротивление эквивалентного активного двухполюсника, которое определяется из выражения 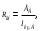 где Iкз.А– ток короткого замыкания двухполюсника (измеряется при R2 =0, либо определяется как алгебраическая сумма токов I1 и I2 при R2 =0). Контрольные вопросы 1 Какие электрические цепи называются линейными? 2 Дайте определение активных и пассивных элементов и участков электрической цепи. 3 Как изменится потенциальная диаграмма, если за базисную принять другую точку электрической цепи? 4 Запишите второй закон Кирхгофа для исследуемой электрической цепи, указав направление токов. 5 Используя принцип суперпозиции, запишите для исследуемой схемы выражения для определения токов. 6 Сформулируйте теорему об активном двухполюснике и поясните на исследуемой схеме. 7 Как экспериментально определяется входное сопротивление пассивного двухполюсника Rвх (т.е. Rвн эквивалентного генератора)? |
