УАУ. Лр21. Лабораторная работа 1 Кобеидзе Николай Пример П1

• Название: Лабораторная работа 1 Кобеидзе Николай Пример П1
• Дата: 12.04.2023
• Размер: 274.43 Kb.
• Имя файла: Лр21.docx
• Тип: Лабораторная работа; #1056304

Лабораторная работа 1

Выполнил: Кобеидзе Николай

Пример П1:

Код: y = trimf( x, [3 6 8]) ;

plot(x, y);

xlabel ( 'trimf(x,P), P = [3 6 8] ');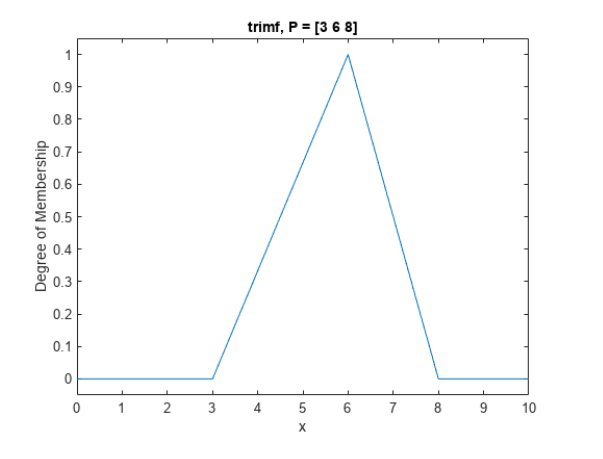



Рис 1. Результат

Пример П2:

Код: x=0:0.1:10;

y= gaussmf (x, [ 2 5]);

plot(x,y);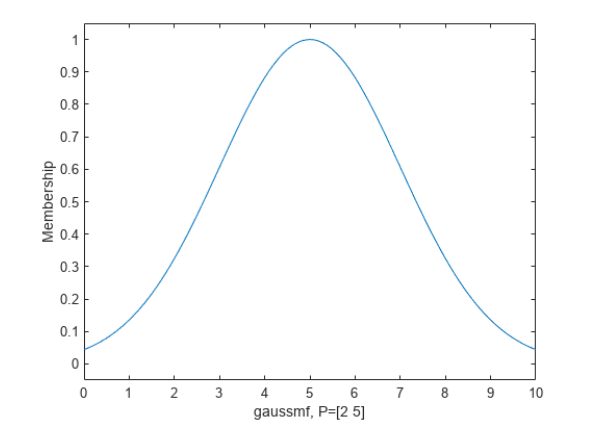



Рис 2. Результат
Пример П3:

Код: x=(0: 0.1: 10)';

y1=gauss2mf(x, [2 4 1 8]);

y2=gauss2mf(x, [2 5 1 7]);

y3=gauss2mf(x, [2 6 1 6]);

y4=gauss2mf(x, [2 7 1 5]);

y5=gauss2mf(x, [2 8 1 4]);

plot(x, [y1 y2 y3 y4 y5 ]);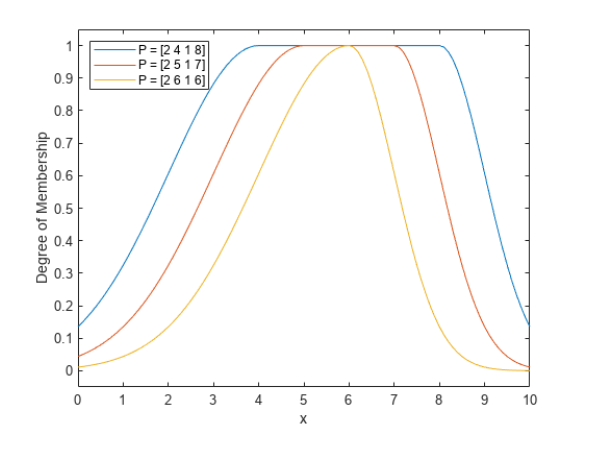



Рис 3. Результат

Пример П4:

Код: x = 0 : 0.1 : 10;

y = gbellmf (x, [2 4 6]) ;

рlot(х, у);

xlabel (' gbellmf, P = [2 4 6] ')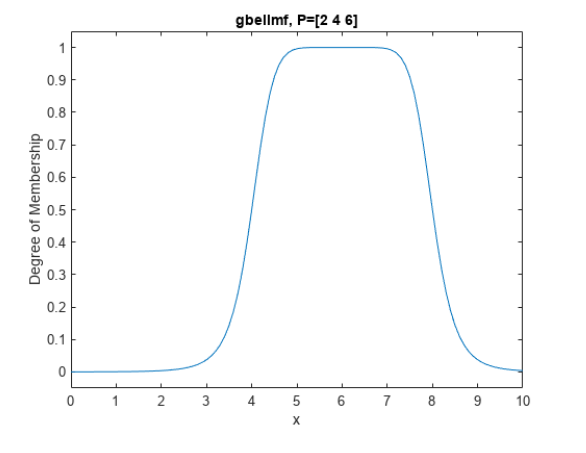



Рис 4. Результат

Пример 5:

Код: x = 0 : 0.1 : 10;

subplot (1,3,1) ;

y=sigmf (x, [2 4 ])

plot (х, у) ;

xlabel ( ' sigmf, Р = [2 4]')

subplot (1,3,2);

y= dsigmf (x, [5 2 5 7 ]) ;

plot (х, у) ;

xlabel ( 'dsigmf, Р = [5 2 5 7]');

subplot (1,3,3);

y = psigmf (x, [2 3 -5 8]);

plot (х, у) ;

xlabel (' psigmf, Р = [2 3 -5 8]');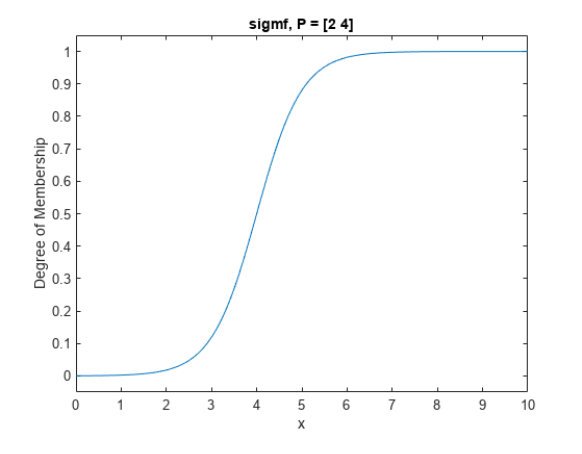



Рис 5. Результат

Пример 6:

Код: x=0:0.1:10;

subplot(1,3,1);

y=zmf(x, [3 7]);

plot(x,y);

xlabel('zmf, P=[3 7]');

subplot(1,3,2);

y=pimf(x, [1 4 5 10]);

plot(x,y);

xlabel('pimf, P=[1 4 5 10]');

subplot(1,3,3);

y=smf(x, [1 8]);

plot(x,y);

xlabel('smf, P=[1 8]');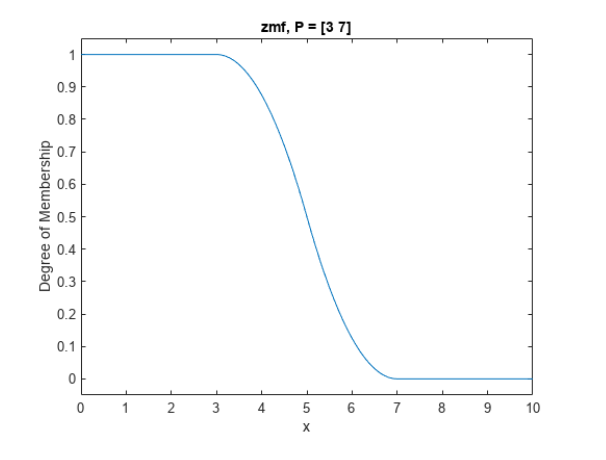



Рис 6. Результат

Пример 7:

Код: x=0:0.1:10;

subplot(1,2,1);

y1=gaussmf(x,[3 5]);

y2=gaussmf(x,[3 7]);

y3=min([y1;y2]);

plot(x, [y1;y2],':');

hold on;

plot(x, y3);

hold off;

subplot(1,2,2);

y4=max([y1;y2]);

plot(x, [y1;y2],':');

hold on;

plot(x, y4);

hold off;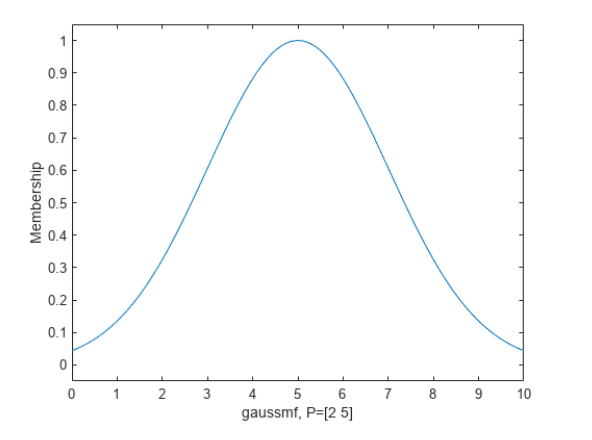



Рис 7. Результат

Пример 8:

Код: x=0:0.1:10;

subplot(1,2,1);

y1=gaussmf(x,[3 5]);

y2=gaussmf(x,[3 7]);

y3=prod([y1;y2]);

plot(x, [y1;y2],':');

hold on;

plot(x, y3);

hold off;

subplot(1,2,2);

y4=probor([y1;y2]);

plot(x, [y1;y2],':');

hold on;

plot(x, y4);

hold off;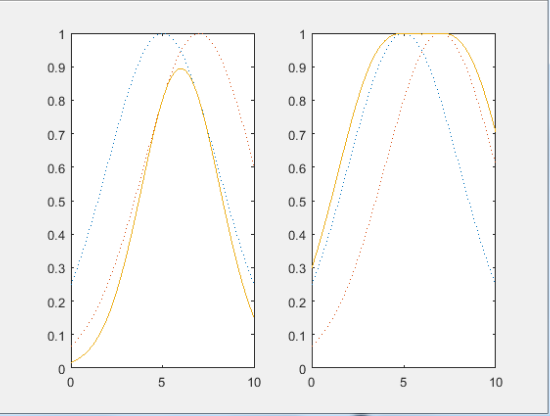



Рис 9. Результат

Пример 9.

Код: subplot(1,1,1);

x=0:0.1:10;

y1=gaussmf(x,[3 5]);

y=1-y1;

plot(x,y1,':');

hold on;

plot(x, y);

hold off;

Контрольные вопросы:

1. 
   Что такое нечеткое множество и каково его основное от­личие от обычного (четкого) множества? - Нечеткое множество представляет собой совокупность элементов произвольной природы, относительно которых нельзя точно утверждать- обладают ли эти элементы некоторым характеристическим свойством, которые используются для задания нечеткого множества.
   

2. 
   Что такое функция принадлежности? - Функцией принадлежности (membership function) называется функция, которая позволяет вычислить степень принадлежности произвольного элемента универсального множества нечеткому множеству. Следовательно, область значений функции принадлежности должна принадлежать диапазону [0, 1].
   

3. 
   Какие конъюнктивные и дизъюнктивные операторы вы знаете? –
   

• 
  ИЛИ || – логическое сложение (дизъюнкция) – OR
  
• 
  И && – логическое умножение (конъюнкция) – AND
  
• 
  НЕ! – логическое отрицание (инверсия) – NOT