Лабораторная работа 1 квантование радиосигналов Рязань 2022 г. Цель работы
 Скачать 1.03 Mb. Скачать 1.03 Mb.
|
|
МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РФ РЯЗАНСКИЙ ГОСУДАРСТВЕННЫЙ РАДИОТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ ИМЕНИ В.Ф.УТКИНА Кафедра РТС Лабораторная работа №1 «КВАНТОВАНИЕ РАДИОСИГНАЛОВ» Рязань 2022 г. Цель работы: Целью работы является исследование шумов и помех, возникающих в аналого-цифровом преобразователе вследствие нелинейности, а также наличия источников теплового шума. Теоретические сведения: Квантование сигнала заключается в округлении – замене аналогового значения сигнала ближайшим уровнем квантования или усечении – замене ближайшим меньшим уровнем квантования. Разность между входным аналоговым сигналом и выходным цифровым сигналом составляет ошибку и обычно представляется как некоторый шум квантования. При равномерном квантовании с шагом h можно считать, что шумы квантования распределены равномерно на интервале h и имеют среднее значение, равное нулю при округлении и равное h / 2 при усечении. Дисперсия шума квантования, приведенная к входу АЦП, в обоих случаях одинакова и равна /12 2 PшАЦП h . Описание программы моделирования: Исходными данными для проведения вычислительного эксперимента являются: 1) число уровней квантования АЦП – устанавливается равным nАЦП NАЦП 2 , 9 2) частота дискретизации сигнала д f , кГц, 3) частота гармонического сигнала 0 f , кГц, 4) полоса частот узкополосного дизера диз f , кГц, 5) параметр дифференциальной нелинейности hдиф , уровней, 6) параметр интегральной нелинейности инт h , уровней, 7) среднеквадратичное значение дизера диз , уровней, 8) амплитуда гармонического сигнала Am , уровней, 9) среднеквадратичное значение теплового шума ш , уровней, 10) число отсчетов входного сигнала N . В лабораторной работе используется входной сигнал АЦП в виде: гармонического колебания с частотой 0 f , амплитудой Am уровней. Тепловой шум приемника моделируется в виде независимых отсчетов случайных величин с гауссовским распределением, нулевым средним и среднеквадратичным значением ш . Дизер формируется в виде гауссовского случайного процесса, состоящего из N гармоник, являющимися комплексными гауссовскими случайными величинами, независимыми друг от друга. Из всего спектра гармоник выделяется область частот д 0...f , которая образует низкочастотный дизер. Аналого-цифровой преобразователь представлен как безынерционный нелинейный преобразователь ступенчатого вида с характеристикой преобразования f x. Дифференциальная нелинейность описывается случайным независимым от уровня к уровню изменением шага квантования по равномерному закону. Максимальное отклонение шага квантования, выраженное числом уровней, задается параметром дифференциальной нелинейности hдиф . Интегральная нелинейность описывается изменением среднего значения переходной характеристики по закону: инт инт NАЦП f x f x h sin 20x . При моделировании фиксируется выход сигнала за апертуру АЦП, что оценивается средним числом выбросов сигнала. Результат аналого-цифрового преобразования преобразуется в спектральную форму с помощью БПФ функции MatLab. Оценка шумов квантования производится по спектру выходного сигнала, а также по среднеквадратическому значению преобразованного сигнала в полосе частот, не 10 совпадающей с полосой частот сигнала. Необходимо помнить, что при вводе числовых данных в программу MatLab используется десятичная точка, например 6.1. Для более удобного отсчета данных на графиках используется логарифмическая шкала, для включения «сетки» которой целесообразно увеличивать размер рисунков. Экспериментальная часть: Пункт 1. Определение уровня шума квантования. F0= 200+N*10=200 + 5*10=250 кГц Fд= F0*4= 250*4= 1000 кГц  Пункт 2.Пронаблюдаем форму спектра выходного сигнала АЦП.  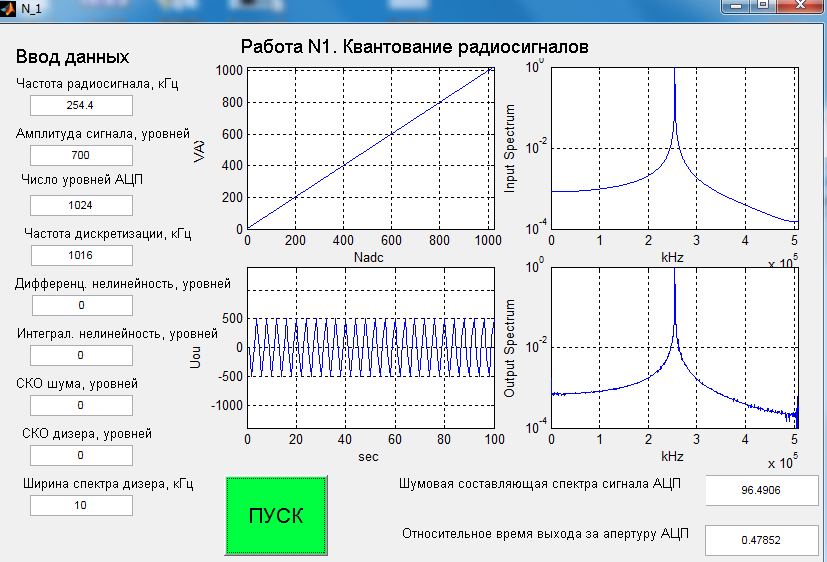   Вывод: с увеличением амплитуды входного сигнала отношение сигнал-шум уменьшается, так как ненормированное среднеквадратичное значение шумовой составляющей спектра выходного сигнала АЦП увеличивается быстрее. Пункт 3.Исследование влияния дифференциальной нелинейности на уровень шума. При 0.5  Изменение значения дифф. нелинейности При 100  При 1000  При 0.111 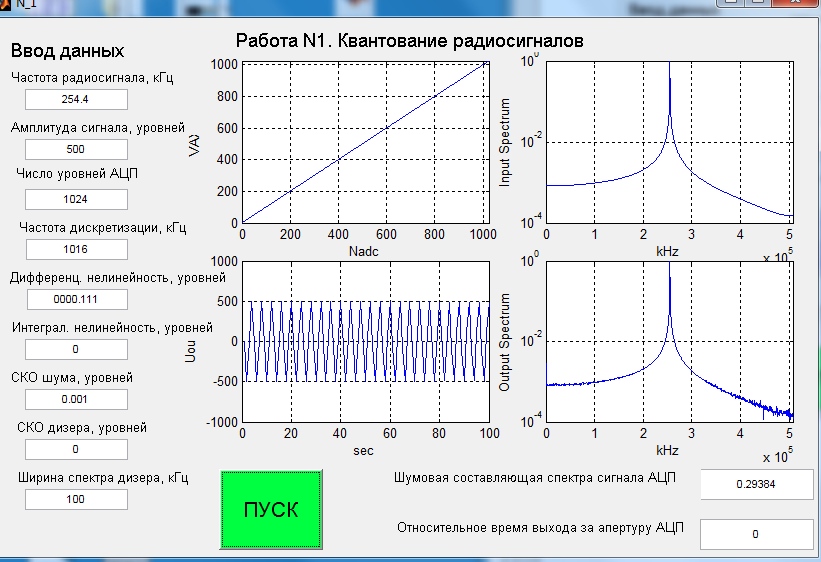 Вывод: на зависимости видим уменьшение ненормированного среднеквадратичного значения шумовой составляющей спектра выходного сигнала АЦП, рассчитанного в полосе частот, где сигнал отсутствует при увеличении дифференциальной нелинейности. Пункт 4. Исследование влияния интегральной нелинейности на уровень шума. F0=79 кГц( Для пунктов 4,5,6)  Df=    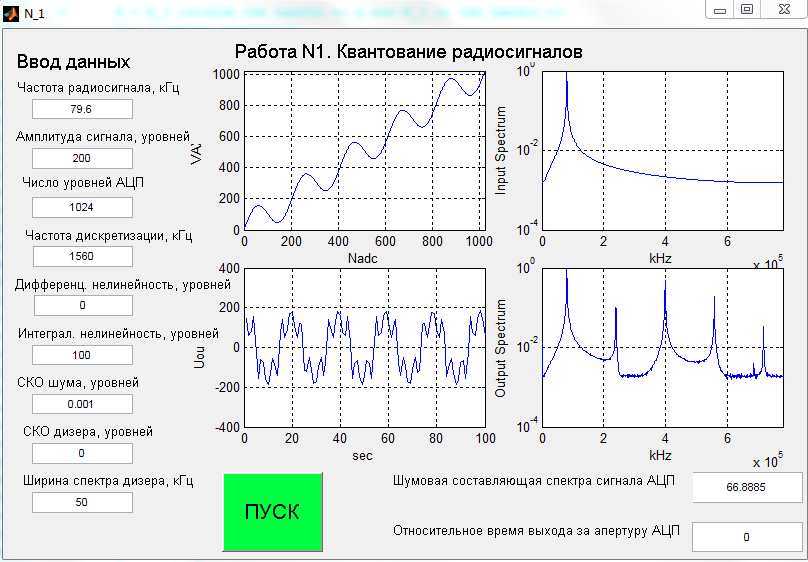 Вывод: на зависимости видим уменьшение ненормированного среднеквадратичного значения шумовой составляющей спектра выходного сигнала АЦП, рассчитанного в полосе частот, где сигнал отсутствует при увеличении интегральной нелинейности. Пункт 5.Исследование влияния широкополосного дизера на свободный динамический диапазон. В качестве широкополосного дизера используется тепловой шум.   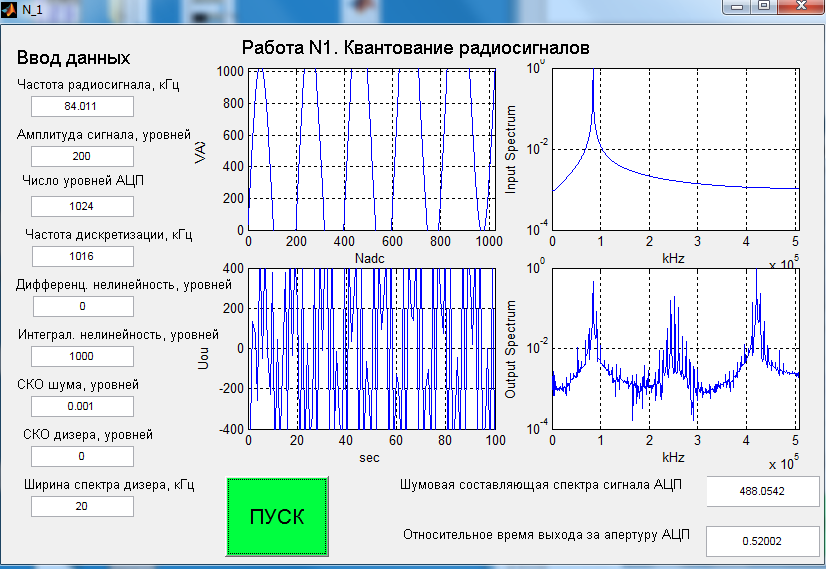  Вывод: увеличение амплитуды дизера может быть использовано для уменьшения в некоторых пределах ошибок, вносимых интегральной нелинейностью. Однако сигналы, намного превышающие уровни дифф. и интеграл. нелинейности, могут уменьшить используемый динамический диапазон АЦП. Пункт 6. Исследование влияния низкочастотного дизера на свободный динамический диапазон. В качестве низкочастотного дизера используется внеполосный шум    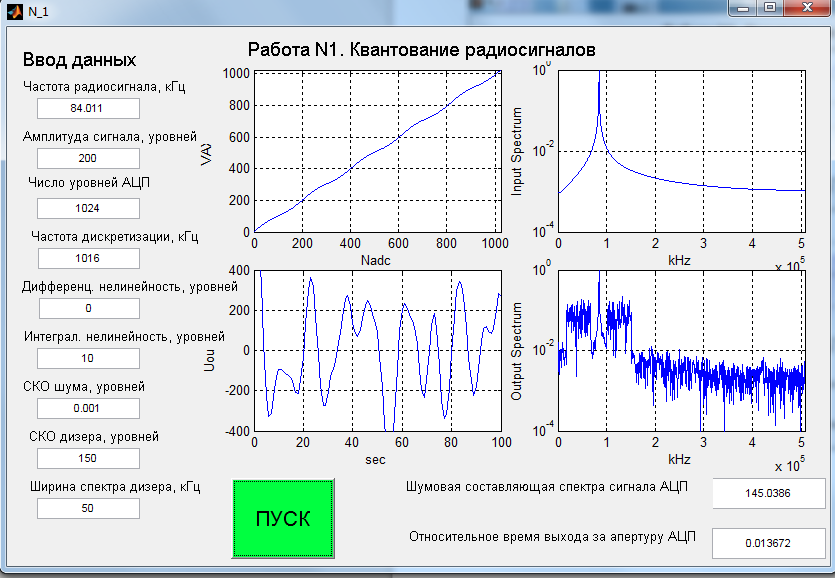 Вывод: увеличение амплитуды дизера может быть использовано для уменьшения в некоторых пределах ошибок, вносимых интеграл. нелинейностью. Вывод: в данной работе мы исследовали шумы и помехи возникающие в АЦП в результате нелинейности, разобрались с понятием дизера и его влияния на свободный динамический диапазон, а также с источником возникновения теплового шума. |
