йцу. Лабораторная работа 1 Линейные алгоритмы
 Скачать 246.24 Kb.
|
|
Лабораторная работа № 1 Линейные алгоритмы Лабораторная работа посвящена основам составления алгоритмов и базовым понятиям языка программирования С++. Затрагиваются такие понятия как программа, переменная, тип данных, операции консольного ввода и вывода, простейшие математические операции. Задачи 1.С горы начинают скатываться сани с ускорением 0,5 м/с2. Какой путь проходят сани, если скорость их в конце горы 36 км/ч. 2.Даны два числа. Найти среднее арифметическое их квадратов и среднее арифметическое их модулей. 3.Дана длина ребра куба. Найти площадь грани, площадь полной поверхности и объём этого куба. 4.Парашютист раскрыл свой парашют на высоте 1 км от поверхности Земли и далее двигался прямолинейно со скоростью 7 м/с по вертикали вниз. На каком расстоянии от поверхности Земли он находился через 1 минуту после раскрытия парашюта. 5.Найти длину окружности и площадь круга заданного радиуса r. 6.Найти площадь кольца, внутренний радиус которого равен r1, а внешний радиус равенr2 (r1 7.Лодка движется перпендикулярно берегу реки. Её скорость относительно воды равна 2 м/с. Определите время движения лодки к другому берегу, если ширина реки 80 м, а скорость течения 1,5 м/с. 8.Дана длина окружности. Найти площадь круга, ограниченного этой окружностью. 9.Дана сторона равностороннего треугольника. Найти площадь этого треугольника, радиусы вписанной и описанной окружностей. 10.Найти периметр и площадь равнобедренной трапеции с основаниями a иb (a >b) и угломβ при большем основании (угол задан в градусах). 11.Какую скорость приобретает после прохождения пути 200 м электропоезд, начинающий равноускоренное прямолинейное движение с ускорением 1,25 м/с2. 12.Найти расстояние между двумя точками с заданными координатами (x1,y1) и (x2,y2). 13.Найти решение системы уравнений вида: a1x + b1y = c1, a2x + b2y = c2 заданной своими коэффициентами a1,b1,c1,a2,b2,c2, если известно, что данная система имеет единственное решение. 14.Скорость первого автомобиля v1 км/ч, второго —v2 км/ч, расстояние между ними s км. Определить расстояние между ними через t часов, если автомобили первоначально движутся навстречу друг другу. 15.Человек переплывает реку шириной 100 м по прямой, перпендикулярной её берегам. Скорость пловца относительно берега 0,3 м/с, скорость течения 0,4 м/с. Какое расстояние преодолевает пловец относительно воды. 16.Скорость лодки в стоячей воде v км/ч, скорость течения реки u км/ч (u 17.Найти длину грани a правильного12-угольникавписанного в окружность радиусом  18.После удара о поверхность Земли мяч движется вертикально вверх со скоростью 15 м/с. Найдите координату мяча над поверхностью Земли через 1 секунду и через 2 секунды после начала движения. 19.Определить число сторон правильного n-угольника со стороной a, описанного вокруг окружности радиусом  20.Определить центральный угол δ , соответствующий длине дуги l окружности радиусом r  21.Прямоугольный треугольник задан координатами вершин (x1,y1), (x2,y2), (x3,y3). Найти значение синуса острого угла. 22.Прямоугольный треугольник задан координатами вершин (x1,y1), (x2,y2), (x3,y3). Найти значение тангенса острого угла. 23.Прямоугольный треугольник задан координатами вершин (x1,y1), (x2,y2), (x3,y3). Найти значение косинуса острого угла. 24.Дана сторона a и два угла треугольника, напримерβ и γ . Найти третий угол и остальные две стороны. Использовать теорему о сумме углов треугольников и теорему синусов. 25.Даны две стороны, например a и b, и угол γ между ними. Найти остальные два угла и третью сторону. Для решения использовать теорему косинусов и/или теорему синусов. 26.Найти угол параллелограмма α , если известны его стороны a и b , а также его площадь S, если формула вычисления площади: S=a b sinα . 27.Вычислить значения функций:  28.Вычислить площадь кругового сегмента, не равного полукругу по формуле  где r – радиус круга, α – градусная мера центрального угла (α<180°), который содержит дугу этого кругового сегмента, SΔ – площадь треугольника с вершинами в центре круга и в концах радиусов, ограничивающих соответствующий сектор. 29. Вычислить координаты точки, делящей отрезок a1a2 в отношении n1:n2 по формулам:  30. Вычислить координаты центра тяжести трёх материальных точек с массами m1 ,m2 ,m3 и координатами (x1 , y1), (x2 , y2), (x3 , y3) по формулам:  31.Вычислить медианы треугольника со сторонами a,b,c по формулам:  32. Вычислить значение функции y=ae−ax sinωx при x= (π /2−ϕ) /ω . 33. Вычислить площадь поверхности  и объём усечённого конуса.34.Вычислить высоты треугольника со сторонами a,b,c по формулам:  35.Определить высоту треугольника, если его площадь равна S, а основание больше высоты на величину a. Лабораторная работа № 2 Циклы и ветвления Лабораторная работа посвящена алгоритмам, реализующим циклы и ветвления, и операторам языка С++, позволяющим описывать такие алгоритмы. Используются циклы с предусловием, с постусловием, цикл «for», условный и тернарный операторы, оператор множественного выбора. 1. Найти U - первый отрицательный член последовательности: cos(ctg(n)) , n=1,2,3... 2. Вычислить y-первое из чисел:  меньшее по модулю 10−4 .3. Вычислить S — сумму квадратов всех целых чисел, попадающих в интервал: (ln x ,ex) при x>1 . 4. Если среди чисел sin (xn) , где n=1…30 , есть хотя бы одно отрицательное число, то переменной t присвоить это число, а иначе – значение π . 5.Дана последовательность из 100 целых чисел, созданная генератором случайных чисел. Определить, со скольких отрицательных чисел она начинается. 6.Вычислить:  7.Вычислить:  8.Вычислить 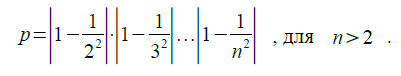 9.Определить, является ли заданное натуральное число палиндромом, т.е. таким, десятичная запись которого читается одинаково слева направо и справа налево (например: 30303, 1441). 10.Сгенерировать 100 случайных вещественных чисел. Вычислить: а) разность между максимальным и минимальным элементами; б) произведение максимального и минимального элементов. 11.Дана последовательность чисел 1…N . Вывести на печать все числа последовательности, которые являются степенью 3, 5, 7. 12. Определить, попадает ли точка с координатами x0 , y0 в круг радиусом r . Уравнение окружности r2=x2+ y2 . Вывести на экран сообщение, если точка лежит внутри круга, за его пределами или на его границе. 13.Вычислить значение: 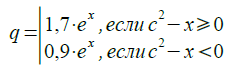 14.Определить, в каком квадранте находится точка с координатами x,y, и вывести на печать номер квадранта. 15.Вычислить корни квадратного уравнения вида  16.Вычислить значение функции: 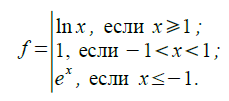 17. Вычислить и вывести на экран значения функции y = a3/ (a2 + x2 ) при x , изменяющимся от 0 до 3 с шагом 0,1. 18. Вычислить: 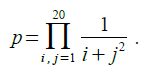 19. Вывести на экран положительные значения функции  при n=1…50. 20.Определить, является ли заданное натуральное число совершенным, т.е. равным сумме всех своих (положительных) делителей, кроме самого этого числа (например, число 6 совершенно: 6 = 1 + 2 + 3). 21.Найти наименьшее значение функции  в интервале изменения аргументаx от 0 до c с шагом h .22.Вычислить сумму четных и сумму нечетных чисел натурального ряда от 1 до n. 23.Вычислить сумму положительных и сумму отрицательных значений функции,  24. Для функции z=xk /k2 определить k , при котором z становится меньше a . 25.Вычислить:  .26.Определить число, получаемое выписыванием в обратном порядке цифр заданного натурального числа. 27.Найти экстремальное значение функции  при изменении аргументаx от 0 до 4 с шагом h . Функция такого вида имеет один экстремум. Если c>0 , то следует искать минимум, если c<0 , то минимум.28. Рассчитать траекторию движения снаряда по формулам   при постоянных скоростях Vx , Vy. Время t изменяется от нуля с шагом Δt.29.Вычислить значение функции z=x3/y , где y=sin(nx)+ 0,5 . 30.Вокруг равностороннего треугольника со стороной А описана окружность. Вычислить количество сторон описанного многоугольника, при котором его периметр отличается от периметра описанной окружности не более чем на величину ε. 31.Найти сумму цифр заданного натурального числа. 32. Определить с точностью 0,2 точку пересечения функции  с осью x при изменении аргумента x от b0 до bm с шагом 0,2. Сначала следует определить знак функции y при x=b0 . Изменение знака функции является признаком пересечения оси x.33.Определить и вывести на экран трёхзначные натуральные числа, сумма цифр которых равна n (1≤n≤27). 34.Даны координаты (как целые числа от 1 до 8) двух различных полей шахматной доски. Определить, может ли конь за один ход перейти с одного поля на другое. 35.Найти среднее арифметическое и среднее геометрическое действительных положительных корней 100 квадратных уравнений вида:  Лабораторная работа № 3 Одномерные массивы и строки Лабораторная работа посвящена векторным типам данных, понятию одномерных массивов и строк. Рассматриваются такие понятия как линейная память, адресация, указатель, операции разыменования указателя и получения адреса, ASCII-код, терминальный нуль. 1. Проверить, имеется ли в заданном тексте баланс открывающих и закрывающих круглых скобок. 2. Во введённом тексте найти слово, в котором доля гласных (“а”, “е”, “и”) максимальна. 3. Дан целочисленный массив B[n]. Определить, сколько пар (положительное число, отрицательное число) находится в начале массива. 4. Найти наименьшее среди тех элементов массива X, которые не являются элементами массива Y (массивы одномерные). 5. Вычислить и запомнить значения функции  в массиве вещественных чисел Z, где xi - элементы вещественного массива X[50].6. Записать в массив N подряд номера положительных элементов массива A[80], а в массив Z сами положительные числа. 7. Записать подряд в массив B элементы массива A[75], стоящие на чётных местах, а элементы, стоящие на нечётных местах, - в массив C. 8. Скопировать положительные элементы массива X[60] в массив Y, а отрицательные – в массив Z. Элементы в массивах Y и Z располагать подряд. 9. Вычислить сумму элементов массива B[68], стоящих на чётных местах. 10. Вычислить среднее геометрическое элементов s массива C[80], удовлетворяющих условию 1≤ci≤2 . Если таких элементов нет, то считать s=0 . 11. Подсчитать количество положительных и количество отрицательных элементов массива X[75]. 12. Для целочисленного массива A[75] определить, является ли сумма его элементов чётным числом, и вывести на экран “ДА” или “НЕТ”. 13. Подсчитать для массива вещественных чисел X[100] количество элементов, ближайшим целым числом для которых является 1. 14. Вычислить и запомнить значения функции  , где xi , yi - элементы массивов X[55] и Y[55] соответственно.15. Запомнить в массиве A значения n, при которых z>0 для знакочередующейся функции  , а в массиве B – значения n, при которых z≤0 ( n=1..100 ).16. Для массива A[80] вычислить наибольшее и наименьшее значения модуля разности между соседними элементами. 17. Из введённого текста распечатать все слова наименьшей длины. 18. Сохранить в одномерном массиве первые 45 чисел Фибоначчи. 19. Вычислить среднее арифметическое отрицательных элементов массива A[60], полагая, что в массиве есть отрицательные значения. 20. Дана последовательность из 100 различных целых чисел. Найти сумму чисел этой последовательности, расположенных между максимальным и минимальным элементами (в сумму включить оба этих числа). 21. Элементы вещественного массива X циклически сдвинуть на k позиций влево. 22. Во введённом тексте найти самое длинное симметричное слово. 23. Найти максимальное из чисел, встречающееся в заданном целочисленном массиве A[n] более одного раза. 24. Выяснить, сколько различных чисел содержится в заданном целочисленном массиве C[n]. 25. Вывести номера и координаты точек, принадлежащих кругу радиусом r. Координаты точек заданы массивами  26. Дан целочисленный массив D[n]. Определить три наибольших элемента этого массива. 27. Поменять элементы массива Y[60], таким образом, чтобы они располагались в обратном порядке. 28. Составить программу, которая реверсирует каждое слово строки str. 29. Вычислить произведение положительных элементов массива X[100]. 30. Напечатать в алфавитном порядке все различные строчные русские буквы, входящие в заданный текст из 80 литер. 31. Запомнить в массиве Z положительные значения y для монотонно убывающей функции  , если x изменяется от 0 до 10 с шагом 0,1. Отрицательные значения функции не вычислять. Считать, что функция имеет хотя бы один отрицательный элемент.32. В символьный массив D записать цифры целого числа k. 33. Вывести на экран элементы вещественного массива Y[100] и их порядковые номера, при соблюдении условия 0 34. По массиву T, где указана температура каждого дня некоторого невисокосного года, определить m – название месяца с наибольшей среднемесячной температурой. 35. Написать программу печати таблицы умножения в шестнадцатеричной системе счисления. Лабораторная работа № 4 Двумерные массивы и матрицы Лабораторная работа посвящена двумерным и многомерным массивам, представлению их в линейной памяти и способам их обработки. 1. Преобразовать массив S[n][n], n=256, осуществив поворот вокруг его центра на 900 против часовой стрелки. 2. Дана вещественная матрица размером 7х7, все элементы которой различны. Найти скалярное произведение строки, в которой находится наибольший элемент матрицы, на столбец с наименьшим элементом. 3. Вычислить сумму элементов квадратной вещественной матрицы 15х15, находящихся в заштрихованной области.  4. Вычислить произведение элементов квадратной вещественной матрицы 10х10, находящихся в заштрихованной области.  5. Определить, является ли заданная квадратная матрица 10x10 симметричной относительно главной и побочной диагонали. 6. Для заданной вещественной матрицы A[100][100] найти минимум среди сумм модулей элементов диагоналей, параллельных побочной диагонали. 7. Дана целочисленная матрица A[n][m]. Заменить нулями элементы матрицы стоящих на пересечении строк и столбцов, в которых имеется хотя бы по одному нулю. 8. Найти седловые точки матрицы. Седловой точкой называется элемент, являющийся минимальным в строке и максимальным в столбце. 9. В двумерном массиве X[n][m] все числа различны. В каждой строке находится минимальный элемент, затем среди этих чисел находится максимальное. Напечатать индексы этого элемента. 10. Дана матрица A[n][m]. Определить количество «особых» элементов в ней, считая элемент особым, если он больше суммы остальных элементов своего столбца. 11. Заполнить квадратную матрицу размером n×n последовательными целыми числами от 1 до n2 , расположенными по спирали, начиная с левого верхнего угла и продвигаясь по часовой стрелке. 12. Найти наибольшие элементы каждой строки матрицы X[10][20] и записать их в массив Y. 13. Найти среднее арифметическое положительных элементов каждого столбца матрицы X[15][25] при условии, что в каждом столбце есть хотя бы один положительный элемент. 14. Вычислить суммы элементов каждой строки матрицы X[20][20], определить наименьшее значение этих сумм и номер соответствующей строки. 15. Из матрицы X[10][15] построить матрицу Y, поменяв местами строки и столбцы. 16. Переформировать вещественную матрицу A[n][m] таким образом, чтобы её строки располагались по возрастанию их первых элементов. 17. Дана вещественная матрица размером 7х4. Переставляя её строки и столбцы, добиться того, чтобы наибольший элемент (один из них) оказался в верхнем левом углу. 18. Даны целочисленные массивы F[18][23] и J[18]. По массиву F получить массив J, присвоив его k-му элементу значение 1, если k-ая строка массива F симметрична, и значение 0 в противном случае. 19. Написать программу, которая вычисляет определитель квадратной матрицы вещественных чисел 3x3. Значения матрицы вводятся пользователем. 20. Дана квадратная матрица 6x6. Найти матрицу, обратную ей, или установить, что такой не существует. 21. Написать программу, которая во введённой с клавиатуры строке преобразует строчные буквы русского алфавита в прописные за счёт использования двумерной матрицы соответствия T[33][2]. 22. Вычислить сумму положительных элементов каждой строки вещественной матрицы A[10][8]. 23. Написать программу, которая определяет учеников в классе, чей рост превышает значение r. Данные хранить в двумерном массиве. 24. Решить двумя способами следующую задачу: переписать элементы главной диагонали матрицы A[n][n] в одномерный массив B. 25. Определить, является ли заданная целая квадратная матрица 10x10 ортонормированной, т.е. такой, в которой скалярное произведение каждой пары различных строк равно 0, а скалярное произведение каждой строки на себя равно 1. 26. Заданы массивы вещественных чисел A[6][9] и X[9]. Заполнить массив A согласно правилу Aij=Xij. 27. Даны следующие целочисленные массивы A[20][20] и B[19][19]. Получить массив B из массива A удалением n-й строки и k-го столбца. 28. Даны целочисленные массивы C[15][20] и D[15]. По массиву C получить массив D, присвоив его k-му элементу значение 1, если элементы k-й строки массива C упорядочены по убыванию, и значение 0 в противном случае. 29. По заданным коэффициентам   и правым частям  найти решение треугольной системы линейных уравнений: 30. Даны натуральное число n и (построчно) элементы квадратной вещественной матрицы A[5][5]. Вычислить n-ю степень этой матрицы ( A1=A, A2=A⋅A, A3=A2 A, и т.д.). 31. Найти минимальные элементы каждой строки матрицы X[20][20] и поместить их на главную диагональ, а диагональные элементы записать на место минимальных. 32. Определить, является ли заданная целая квадратная матрица 9x9 «магическим» квадратом, т.е. такой, в которой суммы элементов во всех строках и столбцах одинаковы. 33. Определить количество элементов каждого столбца матрицы A[10][20], удовлетворяющих условию −15 34. Переписать первые элементы каждой строки матрицы A[15][25], большие c, в массив B. Если в строке нет элемента, большего c, то записать ноль в массив B. 35. Вычислить сумму элементов матрицы B[20][20], расположенных над главной диагональю и удовлетворяющих условию −3≤bi≤5 . Лабораторная работа № 5 Функции Лабораторная работа посвящена понятию функции, декомпозиции программы при помощи функций, способам передачи параметров в функцию. 1. Описать функцию compare(A,B,n), возвращающую 1, если можно преобразовать квадратную матрицу A размером nxn в матрицу B, отражениями относительно главной и побочной диагонали, и 0 в обратном случае. 2. Описать функцию perim(Ax, Ay, Bx, By, Cx, Cy) вещественного типа, находящую периметр треугольника ABC по координатам его вершин (Ax, Ay, Bx, By, Cx, Cy — вещественные параметры). С помощью этой функции найти периметры треугольников ABC, ABD, ACD, если даны координаты точек A, B, C, D. 3. Напишите рекурсивную функцию печати массива, которая принимает массив и размер массива как аргументы и ничего не возвращает. Функция должна прекращать свою работу и возвращаться, если принимаемый массив имеет нулевой размер. 4. Напишите рекурсивную функцию печати строки в обратном направлении, которая принимает символьный массив, содержащий строку, как аргумент, печатает строку в обратном направлении и ничего не возвращает. Функция должна прекращать свою работу и возвращаться, если обнаружен завершающий нулевой символ. 5. Даны две квадратные вещественные матрицы 10-го порядка. Напечатать квадрат той из них, в которой наименьший след (сумма диагональных элементов). 6. Напишите рекурсивную функцию, которая принимает массив и размер массива как аргументы и возвращает наименьший элемент массива. Функция должна прекращать свою работу и возвращаться, если принимаемый массив имеет один элемент. 7. Описать функцию gauss(A, m, n, i1, i2, x), преобразующую вещественную матрицу A размера mxn следующим образом: из строки i1 вычитается строка i2, умноженная на вещественное число x. Двумерный массив A — входной и выходной параметр, прочие параметры — входные. С помощью этой функции, используя в качестве вспомогательной первую строку, обнулить в остальных строках данной матрицы A размера mxn элементы k-го столбца (число k дано, причем A1k≠0 ). 8. Описать функцию transp(A, m), выполняющую транспонирование квадратной вещественной матрицы A порядка m. Двумерный массив A — входной и выходной параметр, m — входной параметр. Использовать эту процедуру для транспонирования данной матрицы A порядка m. 9. Пусть некоторая функция sum(x, y, z) присваивает вектору z сумму векторов x и y. Описать данную функцию и использовать её для вычисления d=a+b+c . 10. Описать функцию sumCol(A, m, n, k) вещественного типа, вычисляющую сумму элементов вещественной матрицы A размера mxn, расположенных в k-м столбце (если k > n, то функция возвращает 0). Для данной матрицы A размера mxn и трех данных k найти sumCol(A, m, n, k). 11. Описать функцию hexToDec(S) целого типа, которая определяет целое неотрицательное число по его строковому представлению S в 16-ричной системе счисления. Параметр S – массив символов, состоит из символов ['0' – '9', 'A' – 'F'] и не содержит ведущих нулей (за исключением значения '0'). Используя эту функцию, вывести пять чисел, для которых даны их 16-ричные представления. 12. Описать функцию repl(A,B), меняющую местами максимальные элементы матриц A и B произвольного порядка. Считать, что в каждой матрице только один элемент. 13. Описать функцию sort(A), которая принимает в виде параметра строку A, состоящую из трех слов, в каждом из которых от 2 до 6 латинских букв и за каждым из которых следует пробел. Функция sort(A) выводит на печать эти слова в алфавитном порядке. 14. Описать функцию cos1(x,eps) вещественного типа (параметры x, eps — вещественные, eps > 0), находящую приближённое значение функции  В сумме учитывать все слагаемые, большие по модулю eps. С помощью cos1 найти приближённое значение косинуса для данного x при шести данных значениях eps. 15. Описать функцию delIJ(A, m, n, i, j), удаляющую из матрицы А размера mxn строку и столбец, содержащие элемент Aij (если i>m или j>n , то матрица не изменяется). Двумерный вещественный массив A и целые числа m и n являются входными и выходными параметрами, i и j — входные параметры. Дана матрица A размера mxn и числа i, j. Применить к матрице A функцию delIJ и вывести полученную матрицу. 16. Описать функцию factors(a, n, F), находящую разложение натурального числа a на простые множители. Количество множителей возвращается в целой переменной n, а сами множители (в порядке неубывания) — в целочисленном массиве F (n и F — выходные параметры; максимальное число элементов массива F считать равным 15). С помощью этой функции разложить на простые множители пять данных чисел. 17. Описать функцию decToBin(n) строкового типа, которая возвращает строковое представление целого неотрицательного числа n в двоичной системе счисления. Результирующая строка состоит из символов '0', '1' и не содержит ведущих нулей (за исключением представления числа 0). Используя эту функцию, получить двоичные представления данных пяти чисел. 18. Описать функцию fillStr(S, Len) строкового типа, возвращающую строку длины len, заполненную повторяющимися копиями строки-шаблона S (последняя копия строки-шаблона может входить в результирующую строку частично). Используя эту функцию, сформировать по данному числу len и пяти данным строкам-шаблонам пять результирующих строк длины len. 19. Описать функцию smooth(A, n), заменяющую каждый элемент вещественного массива A размера n на его среднее арифметическое со своими соседями («сглаживание массива»). Массив A — входной и выходной параметр, n — входной параметр. С помощью этой функции выполнить пятикратное сглаживание данного массива A размера n, выводя на экран результаты каждого сглаживания. 20. Описать функцию shift(S, k, l), которая преобразует шкалу S, циклически сдвигая её элементы на k позиций влево (l=-1) или вправо (l=1). 21. Описать процедуру swapLine(A, m, n, k1, k2), осуществляющую перемену местами строк вещественной матрицы A размера mxn с номерами k1 и k2 (если k1 или k2 больше m, то матрица не изменяется). Двумерный массив A — входной и выходной параметр, прочие параметры — входные. Используя эту процедуру, поменять для данной матрицы A размера mxn строки с номерами k1 и k2. 22. По заданным 40-элементным вещественным векторам X, Y и Z вычислить значение ω с помощью функции calc(X, Y, Z, m):  m – количество элементов векторов. 23. Описать функцию count(S, T), возвращающую целое значение k. Если в первой половине строки S длиной 60 символов менее 12 цифр и если в последней четверти строки T (60 символов) нет литер от 'a' до 'z', тогда вычислить k – количество литер '*', входящих в среднюю треть строки S. Использовать эту функцию для пяти различных строк S и T. 24. Описать функцию subStr(S, K, L) строкового типа, заменяющую все вхождения подстроки K на подстроку L строки S. Использовать эту функцию для трёх наборов S, K и L. 25. Описать функцию otr(Ax, Ay, Bx, By) вещественного типа, находящую длину отрезка AB на плоскости по координатам его концов:  где Ax, Ay, Bx, By — вещественные параметры. С помощью этой функции найти длины отрезков AB, AC, AD, если даны координаты точек A, B, C, D. 26. По заданным вещественным массивам A, B и C вычислить значение t, используя функцию calc(A, B, C, n), где n=50 количество элементов в каждом из массивов. Функция calc задается следующей формулой:  27. Описать функцию sortDec(A, n), выполняющую сортировку по убыванию массива A из n вещественных чисел. Массив A является входным и выходным параметром. С помощью этой функцию отсортировать массивы A, B, C размера nA, nB, nC соответственно. 28. Описать функции trimL(S), trimR(S) и trim(S), удаляющие в строке S соответственно начальные, конечные, начальные и конечные пробелы. Используя эту функции, преобразовать пять данных строк. 29. Описать функцию  Определить при этом функцию, вычисляющую факториал. 30. По заданным целым массивам X и Y вычислить значение u, используя функцию func(X, Y, m), где m = 20 количество элементов массивов:  31. Описать рекурсивную функцию digits(S) целого типа, находящую количество цифр в строке S без использования оператора цикла. С помощью этой функции найти количество цифр в данных пяти строках. 32. Даны натуральное число p и вещественные квадратные матрицы A, B, и C размером 4x4. Получить (A⋅B⋅C)p , используя функцию mult(A, B) возвращающую результат умножения двух матриц. 33. Даны координаты вершин n треугольников. Определить, какой из них имеет наибольшую площадь. Площадь треугольника вычислять с помощью функции. 34. Описать функцию wordN(S, k) строкового типа, возвращающую k-е слово строки S (под словом понимается набор символов, не содержащий пробелов и ограниченный пробелами или началом/концом строки). Если количество слов в строке меньше k, то функция возвращает пустую строку. Используя эту функцию, выделить из данной строки S слова с номерами k1, k2, k3. 35. Описать функцию sin1(x, eps) вещественного типа (параметры x, eps — вещественные, eps > 0), находящую приближенное значение функции sin(x):  В сумме учитывать все слагаемые, большие по модулю eps. С помощью sin1 найти приближенное значение синуса для данного x при шести данных значениях eps. Требования к оформлению отчета Структура отчета: Титульный лист Цель работы Индивидуальное задание Блок-схемы алгоритмов Идентификаторы (описание переменных) Исходный код программы Скриншоты Заключение Федеральное агентство связи Ордена трудового Красного Знамени федеральное государственное бюджетное образовательное учреждение высшего образования «Московский технический университет связи и информатики» Кафедра Математической кибернетики и информационных технологий Отчет по лабораторной работе № по дисциплине «Языки программирования» Выполнил: студент группы __________ ФИО Проверил: _________________ Москва, 2022 |