Отчет 1 Лаба ОИБ. Лабораторная работа 1 Математические примитивы криптографии по дисциплине Основы информационной безопасности

• Название: Лабораторная работа 1 Математические примитивы криптографии по дисциплине Основы информационной безопасности
• Дата: 29.09.2022
• Размер: 39.67 Kb.
• Имя файла: Отчет 1 Лаба ОИБ.docx
• Тип: Лабораторная работа; #705763

1. 
   Министерство образования и науки Российской Федерации
   
2. 
   Санкт-Петербургский Политехнический Университет Петра Великого
   
3. 
   —
   
4. 
   Институт прикладной математики и механики
   
5. 
   Кафедра «Информационная безопасность компьютерных систем»
   

ЛАБОРАТОРНАЯ РАБОТА № 1

6. 
   «Математические примитивы криптографии»
   
7. 
   
   
8. 
   по дисциплине «Основы информационной безопасности»
   

9. 
   
   
10. 
    
    

Выполнили

студенты гр. 13656 /3 Маяцкий Е.В.

<подпись>

11. 
    
    
12. 
    Преподаватель
    
13. 
    асс. преподавателя Крундышев В.М.
    

<подпись>

14. 
    
    

Санкт-Петербург

2019

1. 
   Цель работы:
   

Приобретение расчетных навыков в модульной арифметике, используемой в криптографических алгоритмах и протоколах, ознакомление с математическими вычислениями, используемыми для сокрытия сообщений на примерах алгоритма шифрования RSA и ранцевой криптосистемы Меркеля-Хеллмана.

2. 
   Выполнение работы:
   

1. 
   Номер учебной группы N_гр.= 13656.
   

Порядковый номер в списке группы N_сп. = 19.

Порядковый номер в алфавите третьей буквы фамилии Ф₃ = 33.

((N_гр +N_cп)¹¹ +Ф₃)(mod 11) = ((13656+19)¹¹ +33)(mod 11) = 2.

2. 
   Исходная строка (Ф.И.О): Маяцкий Евгений Васильевич.
   Зашифрованная строка: Тёеьроп Кзикуоп Зёчосвкзоэ.
   

k=6, m=33.

3. 
   Подсчитываем число A= (N_гр.*(8+N_сп.(mod 7)))² и число В=ЧЧММГГГГ(число, месяц, год рождения):
   

A=(13656*(8+19(mod7)))²=31516190784

B=17082000;

Рассчитываем НОД (наибольший общий делитель):

1. 
   НОД(А, В(mod 95)+900)=НОД (31516190784, 950)
   
2. 
   НОД(А, (В+50)(mod 97)+700)= НОД (31516190784, 759)
   
3. 
   НОД(А, (В+20)(mod 101)+1500,(В-40)(mod 103)+2500)=НОД (31516190784, 1592 , 2528)
   

Алгоритм нахождения НОД делением (Метод Евклида):

a) A=31516190784, B=950

31516190784 mod 950=634

A=950, B=634

950 mod 634=316

A=634, B=316

634 mod 316=2

A=316, B=2

316 mod 2=0

A=2, B=0

Ответ: НОД (31516190784, 950) =2

b) A=31516190784, B=759

31516190784 mod 759=12

A=759, B=12

759 mod 12=3

A=12, B=3

12 mod 3=0

A=3, B=0

Ответ: НОД (31516190784, 759) =3

c) A=31516190784, B=1592, С=2528

31516190784 mod 1592=400

A=1592, B=400

1592 mod 400=392

A=400, B=392

400 mod 392=8

A=392, B=8

392 mod 8=0

A=8, B=0

2528 mod 8=0

Ответ: НОД (31516190784, 1592, 2528) =8

4. 
   Найдём составное число:
   

1. 
   Возьмем N=10003, s=1 и t=5001. Тогда: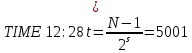
   

• 
  Пусть a=7
  

Проверим 1 условие:

10003/7=1429: k=1 отсюда следует, что 1-ое условие не выполняется, а значит так или иначе N=10003 – составное!

2. 
   Возьмем N=101, s=2 и t=25. Тогда:
   

• 
  Возьмем теперь a=13:
  

Проверим 1 условие:

N не делится на a – да

Проверим 2 условие:

a^t ≡ 1 (mod N), или существует целое k: 0≤k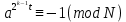


13²⁵ mod 101 ≡ -1 mod 101=100 – да

• 
  Возьмем теперь a=4:
  

Проверим 1 условие:

N не делится на a – да

Проверим 2 условие:

a^t ≡ 1 (mod N), или существует целое k: 0≤k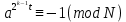


4²⁵ mod 101 ≡ -1 mod 101=100 – да

• 
  Возьмем теперь a=5:
  

Проверим 1 условие:

N не делится на a – да

Проверим 2 условие:

a^t ≡ 1 (mod N), или существует целое k: 0≤k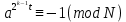


5²⁵ mod 101 ≡ 1 mod 101=1 – да

Вывод:

В результате получаем k =3 – количество повторений, из чего следует:

• 
  Вероятность того, что N составное, не превосходит 4^-k
  
• 
  Вероятность того, что 101 - составное не больше 1/64. Следовательно, 101 вероятно, простое число
  

5. 
   Изучим генерацию ключа в RSA – для этого выберем:
   

• 
  Два простых больших числа: p=383 и q=661. НОД(383,661) =1.
  
• 
  n=p*q=383*661=253163.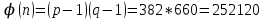
  
• 
  
  
• 
  Пусть e=17. НОД(13,382) =НОД(13,660) =1.
  
• 
  Найдем d, такое, что e*d≡1(mod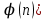
  

НОД(17, 252120)=1

Применим алгоритм Евклида:

Шаг	Большее	Меньшее	Частное	Остаток
1	252120	17	14830	10
2	17	10	1	7
3	10	7	1	3
4	7	3	2	1
5	3	1	3	0
	1	0	-	-

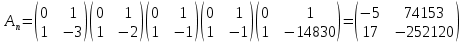Проверим: (17*74153) mod 252120=1

Отсюда получаем: 
Открытый ключ: (e, n) = (17, 253163) 
Секретный ключ: (d, n) = (74153, 253163)

6. 
   Имеем p=383, q=661, n= 253163, ф(n)=252120, e=17, d=74153.
   

Возьмем английское слово teacher и зашифруем – расшифруем, проверив что вышло.

Зашифровываем по формуле x^e mod n:

t = 116 шифр - 38946

e = 101 шифр - 69395

a = 97 шифр - 63652

c = 99 шифр - 130999

h = 104 шифр - 79591

e = 101 шифр - 69395

r = 114 шифр - 18409

Дешифруем по формуле y^d mod n:

шифр - 38946 -> 116

шифр - 69395 -> 101

шифр - 63652 -> 97

шифр - 130999 -> 99

шифр - 79591 -> 104

шифр - 69395 -> 101

шифр - 18409 -> 114

Делаем вывод – полученный код, совпадает с исходным.

7. 
   Подписываем текст цифровой подписью. Для этого используем уже вычисленные в предыдущем примере исходные данные:
   

p=383, q=661, n= 253163, ф(n)=252120, e=17, d=74153, x=teacher
s=x^d mod n

t = 116; s= 212966

e = 101; s= 152274

a = 97; s= 145555

c = 99; s= 232558

h = 104; s= 28696

e = 101; s= 152274

r = 114; s= 219676

x=s^e mod n

s= 212966; x=116

s= 152274; x=101

s= 145555; x=97

s= 232558; x=99

s= 28696; x=104

s= 152274; x=101

s= 219676; x=114

8. 
   Получение сеансового ключа:
   

a=383, x=661, y=150, n=17

A=a^x mod n=8;

B=a^y mod n=4;

B^x mod n=4;

A^y mod n= 4;

Проверка:

(a^x)^y=(a^y)^x= a^xy mod n = 4

9. 
   Алгоритм шифрования RSA:
   

#include

#include

#include

#include

#include
int Euclid(int a, int b)

{
int c;

while (b)

{

c = a % b;

a = b;

b = c;

}

return abs(a);

}
int main()

{

srand((unsigned)time(NULL));

int p;

int q;

printf("Choose any two numbers from 10^2
scanf_s("%d%d", &p, &q);

if (Euclid(p, q) != 1)

{

printf("Enter the requried p,q!\n");

_getch();

return 0;

}

long long int n = p * q;

long long int f = (p - 1)*(q - 1);

long long int e = rand() % 100;

while ((Euclid(e, p - 1) != 1) || (Euclid(e, q - 1) != 1))

{

e = rand() % 100;

}

long long int d = 0, d_sim = 0;

while (d_sim != 1)

{

d += 1;

d_sim = e * d % f;

}

printf("p=%d, q=%d , n=%lli, f=%lli, e=%lli, d=%lli", p, q, n, f, e, d);

const int M = 20;

char a[M];

long long int a_2[M], a_3[M];

long long int *CryptoText = a_2;

long long int *Tdecrypt = a_3;

printf("\nEnter text: ");

gets_s(a);

char *text = gets_s(a);

long long int c;

for (int j = 0; text[j] != '\0'; j++)

{

c = 1;

int i = 0;

while (i < e)

{

c = c * text[j];

c = c % n;

i++;

}

CryptoText[j] = c;

}

printf("\nASCII 1:\n");

for (int j = 0; text[j] != '\0'; j++)

{

printf("text[%d]=%d\n", j, text[j]);

}

printf("\nEncrypted text:\n");

for (int j = 0; text[j] != '\0'; j++)

{

printf("CryptoText[%d]=%lli\n", j, CryptoText[j]);

}
long long int k;

for (int j = 0; text[j] != '\0'; j++)

{

k = 1;

int i = 0;

while (i < d)

{

k *= CryptoText[j];

k %= n;

i++;

}

Tdecrypt[j] = k;

}

printf("\nDecrypted text:\n");

for (int j = 0; text[j] != '\0'; j++)

{

printf("Tdecrypt[%d]=%lli\n", j, Tdecrypt[j]);

}

printf("\nASKII 2:\n");

for (int j = 0; text[j] != '\0'; j++)

{

printf("ASKII [%d]=%c\n", j, (char)Tdecrypt[j]);

}

_getch();

return 0;
}

Алгоритм шифрования и дешифрования Меркеля-Хеллмана:

#include

#include

#include

#include

#include

#include
int Euclid(int a, int b)

{
int c;

while (b)

{

c = a % b;

a = b;

b = c;

}

return abs(a);

}

void PublicSeries(int *PubSeries, int *PriSeries, long long int n, long long int m)

{ printf("\nYour public key:\n");

for (int j = 0; j < 8; j++)

{

PubSeries[j]= (PriSeries[j]*n)%m;

printf("|%d|", PubSeries[j]);

}

}
int cipherText(int x, int *PubSeries)

{

int sum = 0;

int lenInBit = 7;

while (x != 0)

{

if (x % 2 == 1)

{

sum += PubSeries[lenInBit];

}

lenInBit--;

x = x / 2;

}

return sum;

}
int ExEuclid(int n, int m, int &x, int &y)

{

int x1, y1;

if (n == 0)

{

x = 0;

y = 1;

return m;

}

int d = ExEuclid(m%n, n, x1, y1);

x = y1 - (m / n) * x1;

y = x1;

return d;

}
int DeCipher(int userCipher, int *PriSeries)

{

int inc = 1; int sum = 0;

for (int i = 7; i >= 0; i--) {

if (PriSeries[i] <= userCipher) {

sum += inc;

userCipher -= PriSeries[i];

}

inc *= 2;

}

return sum;

}

int main()

{

srand((unsigned)time(NULL));

const int CON = 16;

char a[CON];
printf("Enter text:");

char *text = gets_s(a);

int len=0;

int re=0;

while (text[re] != '\0')

{

len++;

re++;

}

printf("Length=%d", len);

int PriSeries[8];

PriSeries[0]=1+rand()%4;

int k= PriSeries[0];

printf("\nYour private key:");

printf("\n|%d|", PriSeries[0]);

for (int j = 1; j < 8; j++)

{

PriSeries[j]=k+1+rand()%10;

printf("|%d|", PriSeries[j]);

k += PriSeries[j];

}

int m=k+1+rand()%5;

int n=1+rand()%m;

while (Euclid(n, m) != 1)

{

n = 1+rand() % m;

}

printf("\nm=%d, n=%d", m, n);

int PubSeries[8];

PublicSeries(PubSeries, PriSeries, n,m);

int i=0;

int* Cipher;

Cipher = (int*)malloc(len*sizeof(int));

printf("\nCipher:\n");

while (i < len)

{

Cipher[i]= cipherText(text[i], PubSeries);

printf_s("|%d|", Cipher[i]);

i++;

}

printf("\nEnter cipher:");

i=0;

int *userCipher;

userCipher = (int*)malloc(len*sizeof(int));

while (i < len)

{

scanf_s("%d", userCipher + i);

i++;

}

int x, y;

int g = ExEuclid(n, m, x, y);

int d = (x % m + m) % m;

printf("d=%d \n", d);

printf("Decipher:\n");

for (int i = 0; i < len; i++)

{

userCipher[i]= (userCipher[i]*d)%m;

printf_s("|%d|",userCipher[i]);

}

i = 0;

int *ascii;

ascii =(int*)malloc(len*sizeof(int));

printf("\nASCII decipher:\n");

while (i < len)
{

ascii[i] = DeCipher(userCipher[i], PriSeries);

printf_s("|%d| ", ascii[i]);

i++;

}

printf("\nYour word:\n");

for (int j = 0; j < len; j++)

{

printf("%c", ascii[j]);

}
_getch();

return 0;

}

Ответы на контрольные вопросы.

1. 
   Что такое вычет? На чем основан алгоритм цезаря?
   

Число а называется вычетом числа b по модулю m, если разность а — b делится на m (a, b, m > 0 — целые числа). Число а называется вычетом степени n (n ³ 2 — целое) по модулю m, если существует целое число х, такое, что разность xn — a делится на m.

Шифр Це́заря — один из древнейших шифров. При шифровании каждый символ заменяется другим, отстоящим от него в алфавите на фиксированное число позиций. Шифр Цезаря можно классифицировать как шифр подстановки, при более узкой классификации — шифр простой замены.

Шифр назван в честь римского императора Гая Юлия Цезаря, использовавшего его для секретной переписки. Естественным развитием шифра Цезаря стал шифр Виженера. С точки зрения современного криптоанализа, шифр Цезаря не имеет приемлемой стойкости.

Математическая модель

Если сопоставить каждому символу алфавита его порядковый номер (нумеруя с 0), то шифрование и дешифрование можно выразить формулами:

y=x+k(mod n)

x=y-k(mod n)

где x — символ открытого текста, y— символ шифрованного текста, n — мощность алфавита, а k— ключ.

Можно заметить, что суперпозиция двух шифрований на ключах и — есть просто шифрование на ключе . Более общо, множество шифрующих преобразований шифра Цезаря образует группу .

Пример

Шифрование с использованием ключа k = 3. Буква С «сдвигается» на три буквы вперед и становится буквой «Ф». Твердый знак, перемещённый на три буквы вперед, становится буквой «э», и так далее:

Оригинальный текст:

Съешь же ещё этих мягких французских булок, да выпей чаю.

Шифрованный текст

Фэзыя йз зьи ахлш пвёнлш чугрщцкфнлш дцосн, жг еютзм ъгб.

2. 
   Каковы особенности чисел Кармайкла?
   

Числами Кармайкла называются составные числа обладающие следующими свойствами:

При условии что НОД (a,N)=1 N - простое, а – целое, согласно теореме ферма a^(N-1) =1 (mod N).

561 — наименьшее из чисел Кармайкла.

3. 
   Перечислите основные свойства мультипликативной группы вычетов по модулю pq?
   

Группа состоит из ненулевых чисел, меньших n, и взаимно простых с n.Остатки от деления группы на p,q равны соответственно образующим мультипликативных групп полей Fp* и Fp*. Любой элемент кольца может быть представлен в виде a (mod p) и a (mod q). Если a(mod p)=0, а принадлежит идеалу (р) и не является элементом группы (z/nZ)* , при этом а образует в (Z/nZ) мультипликативную группу, изоморфную с Fq*.

4. 
   Почему порядок группы ( Z/nZ )* должен иметь большой простой делитель?
   

Порядок группы — её мощность, то есть количество элементов. Порядок группы равен значению функции Эйлера от n:

#(Z/nZ)*=φ(p)*φ(q)=(p-1)(q-1).

Так как группа состоит из ненулевых чисел, взаимно простых и меньших n, n=pq, то взаимно простых с n чисел — (p-1)(q-1), так как из натуральных чисел меньше n исключаются все, кратные p и q.

5. 
   Опишите алгоритм расчета кодов символов при декодировании шифрограмм согласно алгоритму Меркля-Хеллмана.
   

Предположим, что элементы открытого текста имеют в качестве своих числовых эквивалентов k-разрядные двоичные числа n.

Каждый пользователь выбирает быстрорастущий набор {v₀, …, v_{k – 1}}, целое число   и целое число a, такое что a < 0 < m и НОД(a, m) = 1.

После этого вычисляются b = a ^-1 (mod m) и k-элементный набор {W_i} = {W₀, …, W_k–1}, пределяемый равенствами W_i = av_i (mod m). Пользователь держит числа {v_i}, m, a и b в секрете, а набор {W_i} делает общеизвестным. Таким образом, ключом зашифрования является набор

{W₀, …, W_k–1},

а ключом расшифрования – пара

(b, m),

которая вместе с ключом зашифрования позволяет определить набор {v₀, …, v_{k – 1}}.

Желающий передать сообщение n = (n₀… n_{k– 1})₂ пользователю с ключом шифрования {W_i} вычисляет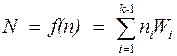



и передает это число.

Чтобы прочесть это сообщение, пользователь сначала находит s = bC:

 ,

поскольку bW_i ≡ bav_i ≡ v_i (mod m). Теперь можно воспользоваться приведенным выше алгоритмом для быстровозрастающего рюкзака и найти единственное решение

(n₀… n_{k– 1})₂ = n задачи о подмножестве {v_i} с суммой равной s.
Вывод.

В данной работе были изучены базовые принципы криптографии, основы модульной арифметики, простейшие способы шифрования передаваемых сообщений, алгоритм шифрования RSA, ранцевую криптосистему Меркля-Хеллмана.

Полученные в ходу выполнения работы навыки пригодятся в последствии при более глубоком изучении криптографии.