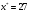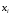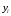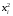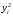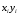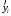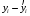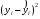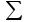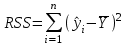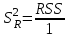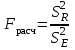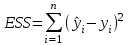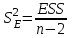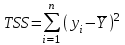Лабораторная работа № 1.pdf. Лабораторная работа 1 Математическое моделирование экономических процессов с помощью парных регрессионных моделей
 Скачать 160.11 Kb. Скачать 160.11 Kb.
|
|
ЛАБОРАТОРНАЯ РАБОТА №1 «Математическое моделирование экономических процессов с помощью парных регрессионных моделей» Данные представлены таблицей значений независимой переменной X и зависимой переменной Y. Задание 1.Вычислить коэффициент корреляции и сделать вывод о тесноте и направлении связи. 2.На уровне значимости α = 0,05 проверить гипотезу о значимости коэффициента корреляции. 3.Составить уравнение парной регрессии Y = b0 + b1X. 4.Нанести данные на чертеж и изобразить прямую регрессии. 5.С помощью коэффициента детерминации R2 оценить качество построенной модели. 6.Оценить значимость уравнения регрессии с помощью дисперсионного анализа. 7.При уровне значимости = 0,05 построить доверительные интервалы для оценки параметров регрессии β1, β0 и сделать вывод об их значимости. 8.При уровне значимости = 0,05 получить доверительные интервалы для оценки среднего и индивидуального значений зависимой переменной Y, если значение объясняющей переменной X принять равным x*.
Решение 1. Вычисление коэффициента корреляции 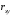 проведем по формуле: проведем по формуле: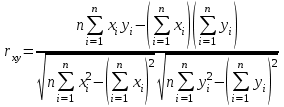 , ,а расчёт параметров b1 и b0 выборочного уравнения парной регрессии соответственно по формулам: 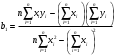 , , 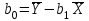 , ,где 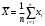 , , 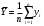 , а n – объём выборки. , а n – объём выборки.Для расчётов удобно использовать следующую таблицу: Таблица 1 Вспомогательная таблица для расчета параметров уравнения парной регрессии
Столбцы 7 – 9 таблицы 1 заполняются после получения выборочного уравнения прямой регрессии и будут необходимы для выполнения последующих пунктов задания. Используя результаты вычислений, представленные в таблице 1, найдём значение выборочного коэффициента корреляции: 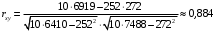 . .Полученное значение коэффициента корреляции свидетельствует о том, что между переменными 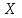 и и 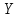 имеется высокая корреляционная связь. Данная связь характеризуется как положительная, т. е. с увеличением одной из переменных значения другой переменной также увеличиваются. имеется высокая корреляционная связь. Данная связь характеризуется как положительная, т. е. с увеличением одной из переменных значения другой переменной также увеличиваются.2. Для оценки значимости коэффициента корреляции следует использовать статистику 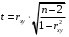 , ,которая в условиях нулевой гипотезы H0:ρxy = 0 имеет распределение Стьюдента с числом степеней свободы, равным n – 2. В нашем случае получаем следующее расчётное значение статистики: 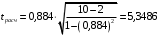 . .Используя таблицы распределения Стьюдента при заданном уровне надёжности 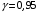 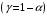 и числе степеней свободы, равном 8, определим критическое значение статистики: и числе степеней свободы, равном 8, определим критическое значение статистики: 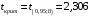 . .Поскольку 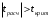 , то нулевую гипотезу о равенстве нулю коэффициента корреляции отвергаем с вероятностью ошибки меньше 5% и делаем вывод о значимости коэффициента корреляции. , то нулевую гипотезу о равенстве нулю коэффициента корреляции отвергаем с вероятностью ошибки меньше 5% и делаем вывод о значимости коэффициента корреляции.3. Для того чтобы составить выборочное уравнение прямой регрессии, необходимо вычислить коэффициенты b1 и b0. Используя результаты расчётов, представленных в таблице 1, находим: 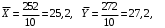 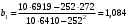 , ,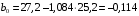 . .Таким образом, получаем следующее регрессионное уравнение: 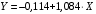 . .4. Прямая регрессии представлена на рисунке 1. 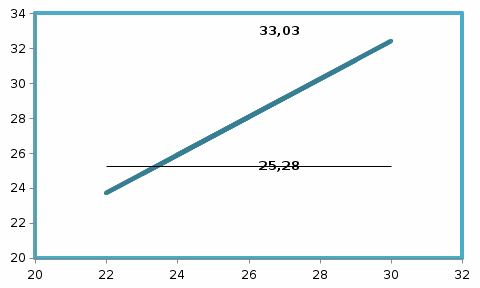 Рисунок 1 – График линейной регрессионной модели 5. Качество регрессионной модели может быть оценено с помощью коэффициента детерминации R2, который определяется формулой: 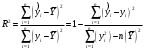 , ,где ŷi = b0 + b1xi, 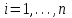 – расчётные (прогнозные) значения величины – расчётные (прогнозные) значения величины 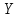 , полученные подстановкой соответствующих значений X в уравнение регрессии. Для вычисления этих значений используются столбцы 7 – 9 таблицы 1. В нашем случае имеем: , полученные подстановкой соответствующих значений X в уравнение регрессии. Для вычисления этих значений используются столбцы 7 – 9 таблицы 1. В нашем случае имеем: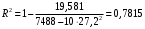 . .Коэффициент детерминации показывает, какую часть вариации (дисперсии) зависимой переменной Y воспроизводит (объясняет) построенное уравнение регрессии. В нашем случае построенное уравнение регрессии на 78,15% объясняет зависимость переменной 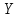 от переменной X. от переменной X.6. Проверка значимости уравнения регрессии заключается в установлении его существенности. Другими словами эта проверка даёт ответ на вопрос о том, насколько можно быть уверенным, что рассматриваемая регрессионная зависимость действительно наличествует в генеральной совокупности, а не является результатом случайного отбора наблюдений. Проверка значимости регрессионной зависимости производится методом однофакторного дисперсионного анализа, где в качестве фактора выступает построенное уравнение регрессии. Результаты дисперсионного анализа принято представлять в виде стандартной таблицы 2. Таблица 2 Результаты дисперсионного анализа
В нашем случае при расчёте сумм квадратов следует принять во внимание следующие равенства: 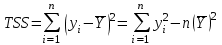 ; ;RSS = TSS – ESS. С учётом результатов, представленных в таблице 1, получим следующие значения: 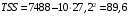 ; ;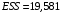 ; ; 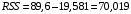 . .Тогда таблица дисперсионного анализа примет вид таблицы 3. Таблица 3 Результаты дисперсионного анализа
При отсутствии линейной зависимости между переменными X и Yстатистика 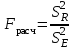 имеет распределение Фишера с числом степеней свободы v1 = 1; v2 = n – 2 = 8. имеет распределение Фишера с числом степеней свободы v1 = 1; v2 = n – 2 = 8.Принимая стандартный 5% уровень значимости, в таблице критических точек распределения Фишера находим 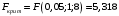 . .Поскольку 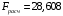 превышает превышает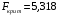 , то делаем вывод о значимости уравнения регрессии. , то делаем вывод о значимости уравнения регрессии.7. Исправленные выборочные оценки стандартных отклонений (ошибок) МНК-коэффициентов регрессии вычисляются по формулам: 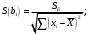 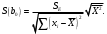 Используя результаты вычислений из предыдущих пунктов, получаем: 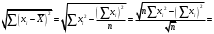 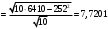 ; ;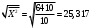 . .Отсюда: 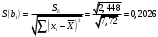 ; ;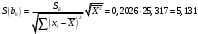 . .Доверительные интервалы для коэффициентов регрессии β1 и β0имеют соответственно вид: 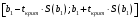 ; ;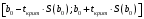 . .Если окажется, что доверительный интервал включает 0, то соответствующий коэффициент регрессии объявляется незначимым. При заданном уровне значимости = 0,05 и числе степеней свободы, равном n – 2, где n – заданный объем выборки (у нас n = 10) критическое значение статистики Стьюдента tкрит = 2,306. Теперь строим доверительные интервалы для β1 и β0 соответственно: 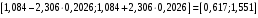 ; ;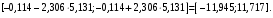 Поскольку интервал коэффициента β1 не включает нулевое значение, а интервал коэффициента β0 включает, делаем вывод о значимом отличии от нуля коэффициента β1 и не значимом коэффициента β0. 8. Интервал для прогноза среднего значения зависимой переменной при значении объясняющей переменной x* (точнее, прогноза 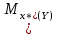 ) по линейному уравнению регрессии имеет вид: ) по линейному уравнению регрессии имеет вид: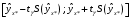 , ,где 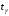 находят по таблицам критических точек распределения Стьюдента для заданных значений и числа степеней свободы v = n – 2 (в случае парной регрессии). Мы уже знаем, что при находят по таблицам критических точек распределения Стьюдента для заданных значений и числа степеней свободы v = n – 2 (в случае парной регрессии). Мы уже знаем, что при 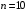 и и 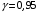 (т.е. (т.е.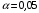 ) ) 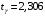 . .Вычисляем 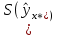 с учетом полученных ранее результатов: с учетом полученных ранее результатов: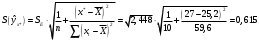 . .Из выборочного уравнения прямой регрессии имеем: 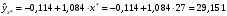 . .Получаем окончательный вид искомого доверительного интервала: 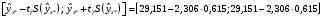 или 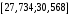 . .Для расчета доверительного интервала возможных индивидуальных значений наблюдений при значении объясняющей переменной x*применяется формула: 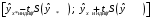 , ,где 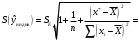 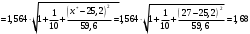 . .Окончательно получаем: 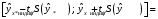 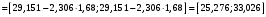 . .ЛИТЕРАТУРА Бабешко Л.О. Основы эконометрического моделирования. – М.: КомКнига, 2006. – 432 с. Бородич С.А. Эконометрика: Учебное пособие. – Мн., Новое знание, 2002. – 408 с. Доугерти К. Введение в эконометрику. – М., 2003, – 402 с. Елисеева И.И. Практикум по эконометрике. – М.: «Финансы и статистика» – 2007. – 344 с. Елисеева И.И. Эконометрика. – М.: «Финансы и статистика» – 2011. – 288 с. Магнус Я.Р. и др. Эконометрика. Начальный курс. – М., Дело, 2000. – 400 с. Тихомиров Н.П, Дорохина Е.Ю. Эконометрика. – М., Экзамен, 2003. – 512 с. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||