Линейная алгебра. Линейная алгебра 5. Лабораторная работа 1 матрицы и действия над ними
 Скачать 132.39 Kb. Скачать 132.39 Kb.
|
|
ЛАБОРАТОРНАЯ РАБОТА 1 «МАТРИЦЫ И ДЕЙСТВИЯ НАД НИМИ» Вычислить матрицу 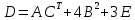 средствами MS Excel. средствами MS Excel. Матрицы А, В, С приведены ниже. Даны матрицы: 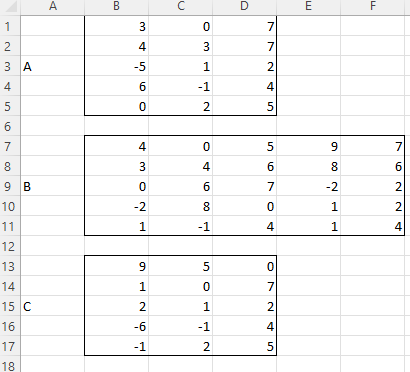 Решение: Транспонируем матрицу С с помощью формулы в ячейке В21: =ТРАНСП(B13:D17) 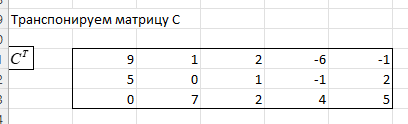 Найдем произведение 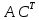 : :=МУМНОЖ(B1:D5;B21#) 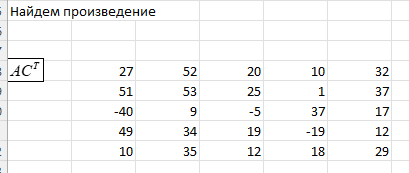 Найдем квадрат матрицы В =МУМНОЖ(B7:F11;B7:F11) 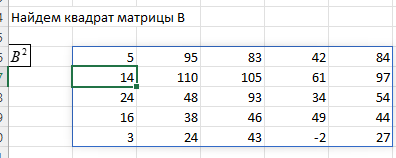 Найдем 4В2 =4*B36# 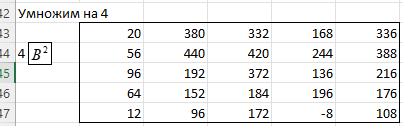 Введем единичную матрицу 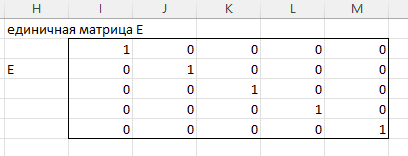 Умножим единичную матрицу на 3: =3*I2:M6 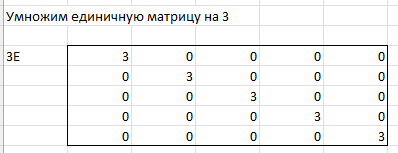 Найдем значение выражения: 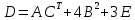 Введем формулу =B28#+B43#+B51# 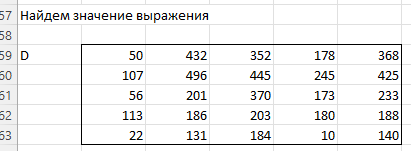 ЛАБОРАТОРНАЯ РАБОТА 2 «ВЫЧИСЛЕНИЕ ОПРЕДЕЛИТЕЛЕЙ И ОБРАТНЫХ МАТРИЦ» 1. Вычислить определители матриц A и B средствами MS Excel. 2. Найти обратную матрицу средствами MS Excel для матриц A и B и выполнить проверку правильности вычислений согласно определению обратных матриц. Даны матрицы А и В 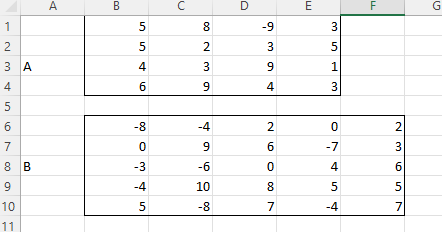 Вычислим определители обеих матриц: Определитель матрицы А =МОПРЕД(B1:E4) Определитель матрицы В =МОПРЕД(B6:F10)  Обратная матрица А =МОБР(B1:E4) 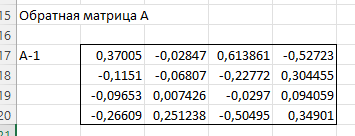 Проверка правильности нахождения обратной матрицы путем умножения на заданную. В результате должна быть получена единичная матрица Е. =МУМНОЖ(B17#;B1:E4) 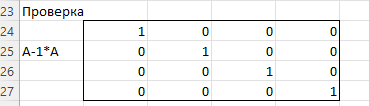 Обратная матрица В =МОБР(B6:F10) 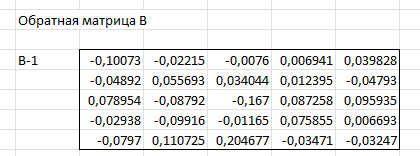 Проверка правильности нахождения обратной матрицы путем умножения на заданную. В результате должна быть получена единичная матрица Е. =МУМНОЖ(H17#;B6:F10) 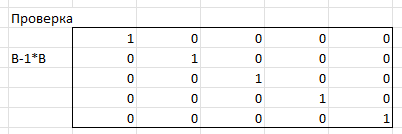 ЛАБОРАТОРНАЯ РАБОТА 3 «СИСТЕМЫ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ» 1. Решить систему линейных алгебраических уравнений: 1) по формулам Крамера; 2) методом обратной матрицы, используя MS Excel; 3) сравнить решения обоими методами между собой; 4) выполнить проверку найденных корней с использованием MS Excel подстановкой в систему уравнений. Дана система уравнений: 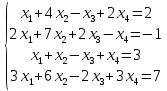 Решение: Составим расширенную матрицу 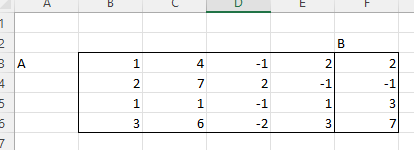 Найдем решение системы методом Крамера. Вычислим определитель основной матрицы. =МОПРЕД(B3:E6) Заменим первый столбец матрицы столбцом из свободных элементов и также найдем определитель. 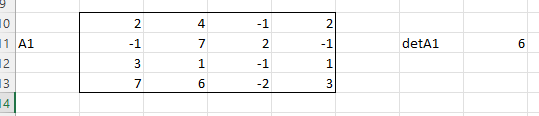 Заменим второй столбец матрицы столбцом из свободных элементов и также найдем определитель.  Заменим третий столбец матрицы столбцом из свободных элементов и также найдем определитель.  Заменим четвертый столбец матрицы столбцом из свободных элементов и также найдем определитель. 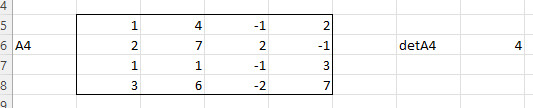 Найдем корни системы путем деления соответствующего определителя с замененным столбцом на определитель основной матрицы: 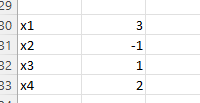 Найдем решение системы методом обратной матрицы. Определим обратную матрицу =МОБР(B3:E6) 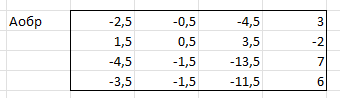 Произведем проверку правильности определения матрицы =МУМНОЖ(L10#;B3:E6) 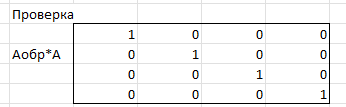 Найдем корни по уравнению Х=А‑1В =МУМНОЖ(L10#;F3:F6) 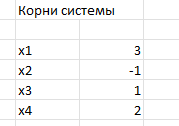 Выполним проверку вычислений путем подстановки найденных значений в исходное уравнение:   |
