Лабораторная работа 1 Определение абсолютной и относительной погрешностей
 Скачать 426.5 Kb. Скачать 426.5 Kb.
|
|
Лабораторная работа № 1 Определение абсолютной и относительной погрешностей приближенных чисел. Оценка погрешностей результата При проведении расчетов необходимо уметь практически оценивать погрешности результата. Разумная оценка погрешности позволяет удерживать оптимальное количество знаков при вычислениях, оптимизируя трудоемкость расчетов. Абсолютная и относительная погрешности вычисляются непосредственно по формулам (1.2.1) и (1.2.2). Количество верных знаков определяется в соответствии с теоремами 1-3 параграфа 1.2. Пример. Округляя заданное число Если, например, Погрешности арифметических операций вычисляются по формулам параграфа 1.3. При этом, например, погрешность суммы большого числа слагаемых, вычисленная по формуле (1.3.1), оказывается сильно завышенной. Поэтому часто применяют статистическую оценку погрешности суммы: где Относительная погрешность разности двух положительных чисел, определяемая по формуле (1.3.3), может быть очень большой, особенно когда эти числа близки между собой. Чтобы избежать потери точности в этом случае часто используют преобразования типа преобразований суммы в произведение. Пример. Найти алгебраическую сумму приближенных чисел и указать ее погрешность. Начнем со слагаемых Для оценки относительных погрешностей результата при умножении и делении формулы (1.3.4) используются редко. Обычно на практике выполняются условия Таким образом, практически при умножении и делении приближенных чисел их относительные погрешности складываются. Пример. Высота Погрешности вычисления значений функций подсчитываются по формулам (1.4.1) и (1.4.2). Если значения функций положительны, то для относительной погрешности можно использовать формулу Для функции одной переменной легко можно определить допустимую погрешность аргумента по допустимой погрешности функции. Для функции нескольких аргументов эта задача решается при введении дополнительного предположения – так называемого принципа равных влияний. При этом полагают, что в формуле (1.4.1) все слагаемые  (Л1.5) (Л1.5)Пример. С каким числом верных знаков должен быть известен свободный член уравнения Будем считать, что коэффициент Если бы оба коэффициента влияли на точность корней, то можно было бы воспользоваться для вычисления 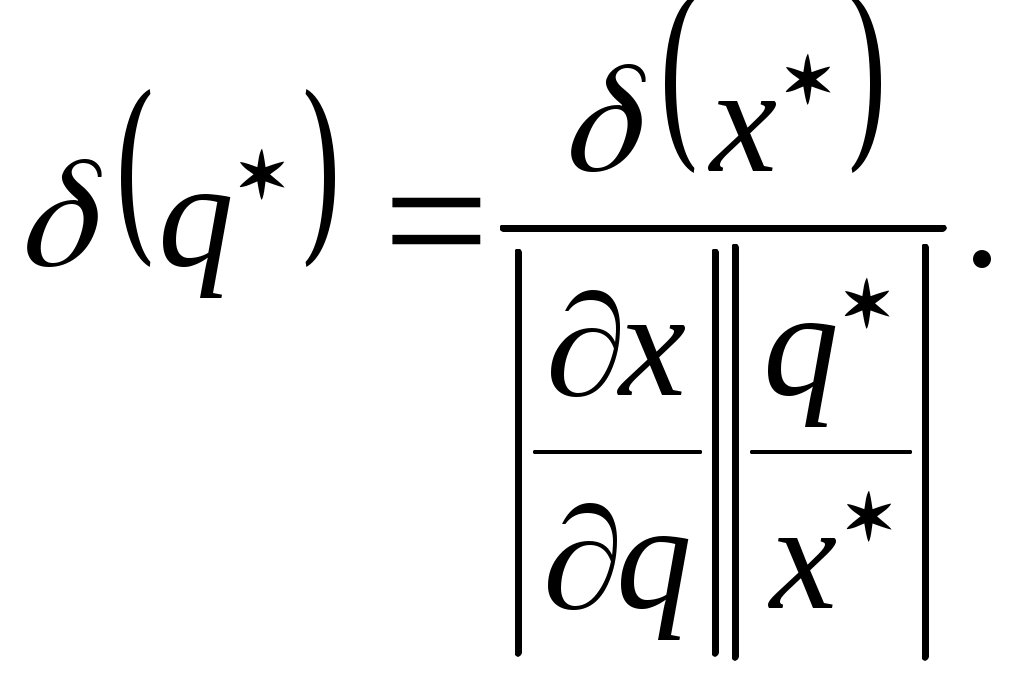 Вычислим Вычислим 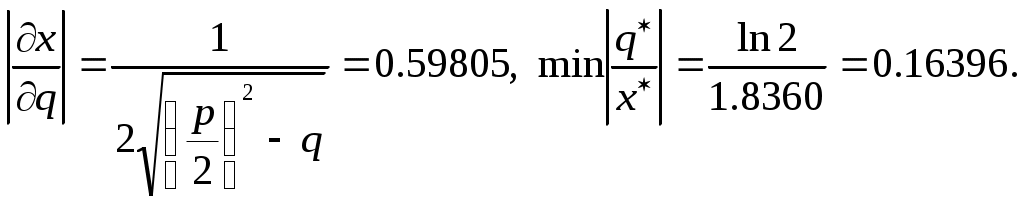 Тогда Тогда Таким образом, для того чтобы получить корни с четырьмя верными знаками, необходимо в исходном уравнении задать Пример. Для определения модуля Юнга по прогибу стержня прямоугольного сечения применяется формула Применение формулы (1.4.2) для относительной погрешности Задание № 1. Величина подъемной силы крыла самолета оценивается по формуле |
