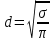Лабораторная работа №2.1. Лабораторная работа 1 определение динамической вязкости воздуха методом пуазейля цель работы
 Скачать 146.52 Kb. Скачать 146.52 Kb.
|
|
ЛАБОРАТОРНАЯ РАБОТА № 2.1 ОПРЕДЕЛЕНИЕ ДИНАМИЧЕСКОЙ ВЯЗКОСТИ ВОЗДУХА МЕТОДОМ ПУАЗЕЙЛЯ ЦЕЛЬ РАБОТЫ 1. Изучение стационарного ламинарного движения несжимаемой жидкости (газа) в изотермических условиях через горизонтальные цилиндрические трубы круглого сечения. 2. Экспериментальное определение динамической вязкости воздуха методом Пуазейля. 3. Количественная оценка средней длины свободного пробега молекул воздуха и их размеров (эффективный диаметр) на основе молекулярно-кинетической теории идеальных газов. ПРИБОРЫ И ПРИНАДЛЕЖНОСТИ 1. Вискозиметр. 2. Секундомер. 3. Термометр. 4. Барометр. ВВЕДЕНИЕ Свойство жидкости (газа) оказывать сопротивление относительному перемещению ее слоев называется ВЯЗКОСТЬЮ. Между слоями жидкости, движущимися с различными скоростями, действуют силы внутреннего трения (силы вязкости). Слоистое движение вязкой несжимаемой жидкости (газа) называется ламинарным. Ламинарное движение возникает при движении жидкости в каналах или трубах небольшого сечения с малыми скоростями, а также при движении очень вязких жидкостей. Рассмотрим, от чего зависят силы вязкого трения. Погрузим в жидкость две параллельные пластинки и будем перемещать верхнюю относительно нижней с постоянной скоростью 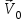 (рис. 1). Для этого необходимо приложить постоянную силу (рис. 1). Для этого необходимо приложить постоянную силу 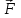 . Так как пластина не получает ускорения, то действие этой силы уравновешивается другой, равной ей по величине и противоположно направленной силой трения . Так как пластина не получает ускорения, то действие этой силы уравновешивается другой, равной ей по величине и противоположно направленной силой трения 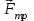 . Такие силы действуют между любыми слоями жидкости при условии, что они перемещаются друг относительно друга. При этом со стороны более быстрого слоя на более медленный слой действует ускоряющая сила, а со стороны медленного на более быстрый – замедляющая. . Такие силы действуют между любыми слоями жидкости при условии, что они перемещаются друг относительно друга. При этом со стороны более быстрого слоя на более медленный слой действует ускоряющая сила, а со стороны медленного на более быстрый – замедляющая.Б 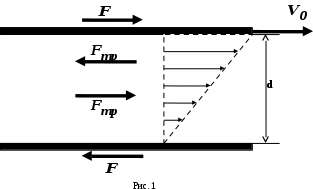 ольшинство жидкостей прилипает к поверхности твердых тел, погруженных в жидкость. Мы будем рассматривать только такие жидкости. Слой, прилегающий к верхней пластине, будет двигаться со скоростью 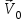 . Нижняя пластина будет испытывать действие вязкой силы в направлении движения верхней пластины и поэтому она должна прийти в движение. Пусть нижняя пластина неподвижна. Для этого к ней необходимо приложить внешнюю силу, направленную против силы вязкого трения и равную ей. Слой жидкости, прилегающий к нижней пластине, будет неподвижен, а скорость вышележащих слоев будет нарастать, как показано на рис. 1. . Нижняя пластина будет испытывать действие вязкой силы в направлении движения верхней пластины и поэтому она должна прийти в движение. Пусть нижняя пластина неподвижна. Для этого к ней необходимо приложить внешнюю силу, направленную против силы вязкого трения и равную ей. Слой жидкости, прилегающий к нижней пластине, будет неподвижен, а скорость вышележащих слоев будет нарастать, как показано на рис. 1.Величина силы вязкого трения зависит от того, как "быстро" меняется скорость слоев с высотой, то есть от величины 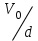 , где d – расстояние между пластинами, от площади поверхности S перемещающихся относительно друг друга слоев, а также от природы и состояния жидкости. В нашем случае можно записать , где d – расстояние между пластинами, от площади поверхности S перемещающихся относительно друг друга слоев, а также от природы и состояния жидкости. В нашем случае можно записать
где величина 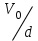 называется градиентом скорости и характеризует изменение скорости поперек потока жидкости, приходящееся на единицу длины; – коэффициент внутреннего трения, называемый динамической вязкостью, зависящий от природы жидкости, температуры и давления. называется градиентом скорости и характеризует изменение скорости поперек потока жидкости, приходящееся на единицу длины; – коэффициент внутреннего трения, называемый динамической вязкостью, зависящий от природы жидкости, температуры и давления.Введем понятие поверхностной плотности вязкого трения. Это сила вязкого трения, приходящаяся на единицу поверхности слоев:
В общем случае распределение (эпюра) скоростиV(x) поперек потока может быть нелинейным (рис. 2). 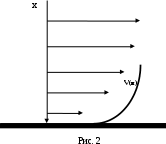 Градиент скорости 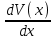 зависит от x, и сила вязкого трения для различных слоев будет функцией x. С учётом направления силы вязкого трения можно записать зависит от x, и сила вязкого трения для различных слоев будет функцией x. С учётом направления силы вязкого трения можно записать
Соотношение (3) называется законом вязкого трения Ньютона. Из (3) можно установить физический смысл коэффициента . Динамическая вязкость численно равна силе вязкости, действующей на единицу площади слоя, при градиенте скорости, равном единице:
Внутреннее трение является причиной того, что для протекания газа (жидкости) через трубу требуется некоторая разность давлений. Разность давлений тем больше, чем больше коэффициент внутреннего трения . Рассмотрим стационарное течение вязкой несжимаемой жидкости (газа) по цилиндрической трубе круглого сечения. Мысленно выделим расположенный вдоль оси трубы цилиндр длинойl и радиусом r (рис. 3). Скорость жидкости в разных точках сечения трубы различна. Она зависит от расстояния до стенок, а градиент скорости есть 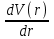 . .С 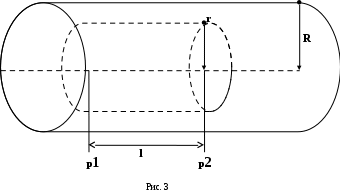 внешней стороны на единицу поверхности цилиндра действует сила вязкости
а на всю поверхность S=2rl рассматриваемого цилиндра – сила 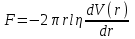 . .Движение происходит с постоянной скоростью, и сила F должна уравновешивать разность сил давления p1 и p2 на торцах цилиндра. 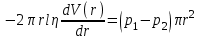 , ,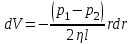 . .Интегрируя, получаем 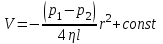 . .У стенок трубы при r = R скорость жидкостиV = 0. Жидкость прилипает к стенкам трубы. Из этого условия находится постоянная, и окончательно для скорости получаем
где p = p1 – p2. Эпюра скорости является параболоидом вращения с меридиальным сечением в виде параболы, которая одинакова для различных сечений трубы. Скорости по сечению трубы растут по квадратичному закону от нуля у стенок до максимального значения на оси трубы: 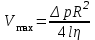 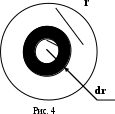 . .Вычислим объемный расход жидкости за секунду через все сечение трубы. Разобьём сечение трубы на тонкие кольца радиусом r и шириной dr (рис. 4). Через площадь кольца dS=2prdr в единицу времени протекает объем жидкости dQ=2prdrV, а через все сечение трубы протекает объем жидкости 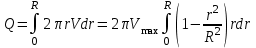 . .Интегрируя, получим закон Пуазейля:
ОПИСАНИЕ УСТАНОВКИ И ЭКСПЕРИМЕНТАЛЬНОЕ ОПРЕДЕЛЕНИЕ ДИНАМИЧЕСКОЙ ВЯЗКОСТИ ВОЗДУХА В лабораторной работе закон Пуазейля используется для экспериментального определения динамической вязкости воздуха:
На опыте необходимо измерить перепад давлений p и секундный объемный расход воздуха Q (м3/с). Параметры трубы R, l должны быть известны. Вязкость воздуха мала, и для ламинарного движения необходимо обеспечить малую скорость и выбрать трубку небольшого сечения капиллярную трубку. С 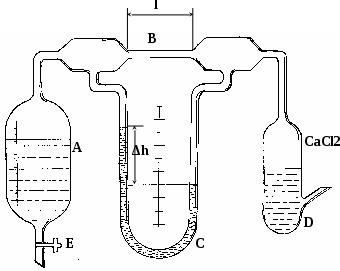 хематично установка для определения вязкости воздуха изображена на рис. 5. Рис. 5 Из аспиратора А выливается вода, давление в нем понижается, и через капиллярную трубку длиной l=0,1 м и радиусом R=10-3 м засасывается воздух, проходящий через осушительный фильтр D с CaCl2 . Разность давлений p на концах трубки В измеряется водяным манометром С. Для измерения секундного расхода воздуха Q аспиратор А заполняют водой, открывают кран Е и выжидают некоторое время, необходимое для установления стационарного течения. В этом случае разность уровней воды h в манометре С будет постоянной. Включают секундомер, одновременно отметив на аспираторе уровень воды. После того как вытечет V=1 л воды, секундомер выключают. Секундный расход воздуха будет равен объему воды, вытекающему из аспиратора за 1 с:
Перепад давлений можно выразить через h:
где = 103 кг/м3 – плотность воды, g=9,8 м/с2 – ускорение силы тяжести. Для динамической вязкости воздуха из (7) с учетом (8) и (9) получаем
или в единицах СИ
Для расчета вязкости надо выразить h в м, t – в с, V – в м3. Результаты измерений и расчета динамической вязкости воздуха заносятся в протокол испытаний. Опыт повторяют 5 раз. КОЛИЧЕСТВЕННАЯ ОЦЕНКА СРЕДНЕЙ ДЛИНЫ СВОБОДНОГО ПРОБЕГА И ЭФФЕКТИВНОГО СЕЧЕНИЯ СТОЛКНОВЕНИЯ МОЛЕКУЛ Механизмы переноса в газах (теплопроводность, вязкость, диффузия) с молекулярно-кинетической точки зрения связаны с тепловым движением молекул и их столкновениями между собой, при которых молекулы обмениваются энергией и импульсом. Согласно молекулярно-кинетической теории газов динамическая вязкость газов выражается как
Здесь – плотность газа (кг/м3); U – тепловая скорость (м/с),
где – эффективное сечение столкновения (м2), n – число молекул в единице объема (м-3). По вязкости газа можно оценить длину свободного пробега 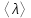 и d. Из (12), учитывая основное уравнение молекулярно-кинетической теории идеальных газов в форме и d. Из (12), учитывая основное уравнение молекулярно-кинетической теории идеальных газов в форме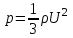 , (15) , (15)получим 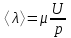 или с учетом (13)
где R = 8,31Дж / (мольК) – универсальная газовая постоянная, Т –абсолютная температура (K), p – давление газа (Па). Будем рассматривать воздух как мономолекулярный идеальный газ с молярной массой 0,029кг/моль. Длина свободного пробега
Из (14), учитывая равенство
и соотношение (16), получаем
где k=1,3810-23 Дж/К постоянная Больцмана. Для воздуха
Измеряя температуру воздуха термометром и атмосферное давление барометром, вычисляем 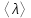 и по формулам (17) и (20). Диаметр молекул воздуха оцениваем по формуле и по формулам (17) и (20). Диаметр молекул воздуха оцениваем по формуле
и сравниваем с табличным значением для молекул N2 и O2: d=310-10м. Результаты измерений и расчетов записать в протокол испытаний. ПРОТОКОЛ ИСПЫТАНИЙ
h=(0.02+0.018)/2=0.0019 м; p =101308 Па; V=0.008 м3; Т=296К; t = 42 сек; Далее вычисляете , 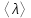 ,, d. (по формулам 11,17,20 и 21. ,, d. (по формулам 11,17,20 и 21. |

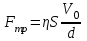 ,
,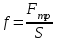 .
.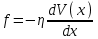 .
. при
при 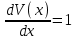 .
.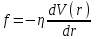 ,
,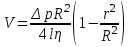 ,
,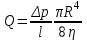 .
.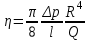 .
.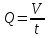 .
.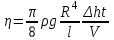
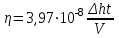 .
.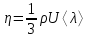 .
.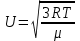 ;
; ,
,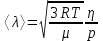 ,
, .
.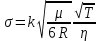 ,
,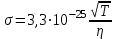 .
.