Лабораторная работа №1. Лабораторная работа 1 определение главных фокусных расстояний собирающей и рассеивающей линз студент группы ээ 12 06
 Скачать 212.5 Kb. Скачать 212.5 Kb.
|
|
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ Федеральное государственное образовательное учреждение Высшего профессионального образования «Чувашский государственный университет им. И.Н. Ульянова» Кафедра общей физики ЛАБОРАТОРНАЯ РАБОТА №1 ОПРЕДЕЛЕНИЕ ГЛАВНЫХ ФОКУСНЫХ РАССТОЯНИЙ СОБИРАЮЩЕЙ И РАССЕИВАЮЩЕЙ ЛИНЗ Выполнил: Студент группы ЭЭ – 12 - 06 Михайлов К.А. Проверил: Егоров В.В. Чебоксары 2007 Приборы и принадлежности: оптическая скамья, собирающая линза, рассеивающая линза, экран. Краткая теория. Линзой называется часть прозрачной, хорошо преломляющей среды, ограниченной от окружающего воздуха кривыми, чаще сферическими поверхностями. Прямая, соединяющая центры кривизны сферических поверхностей С1 и С2, называется главной оптической осью линзы, (рис.1а и б). Тонкими линзами называются такие линзы, у которых толщина С1С2 мала по сравнению с радиусами кривизны, для таких линз можно считать, что точки С1С2 сливаются в одну, которая называется главным оптическим центром линзы. Всякий луч, составляющий малый угол с оптической осью тонкой линзы проходит через оптический центр, практически не преломляясь. Точка пересечения лучей, падающих на линзу параллельно главной оптической оси, называется главным фокусом линзы; расстояние от главного фокуса до оптического центра линзы называется главным фокусным расстоянием линзы. Точка F1 пересечения лучей, падающих на линзу параллельным пучком, составляющим некоторый угол φ (рис.1а) с главной оптической осью называется побочным фокусом. Побочный фокус тонкой линзы лежит в точке пересечения побочной оптической оси CF1, с фокальной плоскостью. Главное фокусное расстояние линзы зависит от радиуса кривизны сферических поверхностей R1 и R2, ограничивающих линзу и от показателя преломления nл вещества линзы и показателя преломления среды nср, в которой находится линза. Для тонких двояковыпуклых линз эта зависимость выражается формулой У всякой линзы имеется два главных фокуса, которые как следует из формулы (1), расположены на одинаковых расстояниях от оптического центра линзы при всяких значениях ее радиуса кривизны. Если радиус кривизны сферических поверхностей одинаковы (R1=R2=R), то формула (1) имеет вид: где n – относительный показатель преломления. Если поместить светящийся предмет на расстоянии d от оптического центра собирающей линзы, то его изображение получится на расстоянии f от него. Эти два расстояния связаны между собой известным соотношением: откуда Если предмет поместить на расстояние d от оптического центра линзы, то как видно из формулы (3), изображение получится на расстоянии f от него, поэтому расстояние f называют сопряженным расстоянию d. Определение фокусного расстояния линзы в основном сводится к использованию формулы (3). Однако в линзах конечной толщины, употребляемых па практике нет одной такой точки, которая обладала бы свойствами оптического центра. Принимая середину линзы за оптический центр ее, мы делаем существенную ошибку. Рассматриваемый ниже способ определения фокусного расстояния по "величине перемещения линзы" свободен от погрешности, обусловленной конечной толщиной; разберем сущность этого способа. Если предмет АВ поместить от экрана Э на расстоянии, больше четырех фокусных расстояний собирающей линзы, то, передвигая линзу, можно найти два такие положения 1 и 2, при которых на экране один раз будет увеличенное изображение А1В1, другой раз – А2В2 (рис.2) – уменьшенное. Обозначим расстояние от оптического центра линзы до предмета и изображения для первого случая через d1 и f1, а для второго случая через d2 и f2. Расстояние от предмета до экрана обозначим через L, а расстояние, на которое нужно передвинуть линзу при переходе из положения 1 в положение 2, через l. Формула (3) для каждого случая можно написать так: Приравнивая равные части последних равенств, получим: или Отсюда получаем равенство: Следовательно: Точно также доказывается, что Учитывая (рис.2), что и принимая во внимание равенство (4) и (5), легко доказать, что Внося эти значения d1 и f1 в формулу (3), получим: Отсюда будем иметь: Из этого выражения следует, что для определения главного фокусного расстояния разбираемым способом нужно измерить расстояние l, на которое надо переместить линзу при переходе из положения 1 в положение 2. Расстояние L и l не связаны с определением оптического центра линзы. Определение фокусного расстояния рассеивающей линзы теми приемами, которые описаны выше, невозможно, т.к. она не дает действительного изображения. Методы, применяемые в этом случае, используют совокупное действие собирающей линзы и рассеивающей линзы. Пусть точка В есть изображение светящейся точки А, получаемой при помощи собирающей линзы L1 (рис.3). Если поставить между линзой L1 и точкой В рассеивающую линзу L2, то изображение светящейся точки А переместиться из точки В в точку С. В следствии обратимости лучей света в линзах можно считать, что светящейся точкой является точка С. Лучи света, распространяющиеся из точки С после преломления в рассеивающей линзе, идут на собирающую линзу по таким направлениям, продолжения которых пересекаются в точке В. В таком случае точка В является мнимым изображением точки С. Следовательно, для рассеивающей линзы Тогда Отсюда получаем значение величины фокусного расстояния рассеивающей линзы: Описание установки. На одном конце оптической скамьи помещено матовое стекло с крессом нитей, освещаемое электрической лампочкой. Вдоль скамьи на ползунках могут перемещаться линза и белый экран. Матовое стекло с крестом нитей служит предметом, от которого получают изображение на белом экране. Положение матового стекла линзы и экрана фиксируется в делениях шкалы соответствующими указателями. Предмет, линзу и экран следует расположить так, чтобы их центры лежали на одной горизонтальной прямой (при горизонтальном положении скамьи). Порядок выполнения работы. ОПРЕДЕЛЕНИЕ ФОКУСНОГО РАССТОЯНИЯ СОБИРАЮЩЕЙ ЛИНЗЫ. Способ 1. Этот способ основан на непосредственном применении формулы (3): измеряются d и f. Помещают экран на достаточно большом расстоянии от предмета. Ставят исследуемую линзу между предметом и экраном; перемещением линзы добиваются отчетливого изображения предмета на экране (увеличенного). Записывают положение предмета, линзы и экрана в делениях шкалы скамьи; вычисляют расстояние от предмета до линзы и от линзы до экрана. Сдвинув линзу, снова делают ее установку на отчетливое изображение предмета, вычисляют d и f. Таких установок делают не менее 5-ти. Находят d′ср и f′ср. Перемещая линзу по скамье находят такое ее положение, при котором на экране получается отчетливое уменьшенное изображение предмета. Не менее 5-ти раз производят отсчеты d и f (также как в п.1). Находят d"ср и f"ср. Обработка результатов измерений. Используя формулу (3) по средним значениям d′ср и f′ср находят главное фокусное расстояние линзы. Аналогично рассчитывают главное фокусное расстояние F" по средним значениям d"ср и f"ср. Вычисляют среднее значение Способ 2 (для собирающей линзы). МЕТОД БЕССЕЛЯ. Фокусное расстояние определяется по "величине перемещения линзы". Помещают экран на расстоянии больше чем 4F, где F – главное фокусное расстояние, определяемое предыдущим опытом. Измеряют это расстояние L (рис.2). Помещают между предметом и экраном линзу и, перемещая ее получают резкое увеличенное изображение предмета на экране. Записывают то деление шкалы n1, против которого стоит указатель, прикрепленный к ползунку линзы. Передвигая линзу, получают отчетливое уменьшенное изображение предмета на экране (экран во время опыта не перемещают). Отмечают по шкале это новое положение линзы – n2, вычисляют расстояние l, на которое пришлось передвинуть линзу при переходе из положения 1 в положение 2: Повторяют опыт несколько раз, смещая и вновь устанавливая линзу для получения одного увеличенного и другого уменьшенного изображения предмета, каждый раз вычисляя l/ Обработка результатов опыта. Определив среднее значение lср по формуле (6) вычисляют величину главного фокусного расстояния. Вычисляют относительную погрешность определения F по формуле: и абсолютную погрешность: По формуле (2) вычисляют радиус кривизны линзы, считая показатель преломления вещества линзы ОПРЕДЕЛЕНИЕ ГЛАВНОГО ФОКУСНОГО РАССТОЯНИЯ РАССЕИВАЮЩЕЙ ЛИНЗЫ. Собирающую линзу L1, фокусное расстояние было определено предыдущими опытами, устанавливают на оптическую скамью на расстоянии от предмета больше 2F1. Поместив на скамью экран, его перемещают до получения на нем отчетливого изображения предмета (оно будет уменьшенным). Записывают положение экрана n1, в делениях шкалы (рис.4). Опыт повторяют не менее 5 раз, не изменяя положение линзы L1. Испытываемую рассеивающую линзу L2 помещают между собирающей линзой L1 и экраном; при этом изображение на экране делается нерезким (размытым). Отодвигая экран от линзы L2, добиваясь получения на нем отчетливого изображения предмета. В делениях шкалы записывают положение линзы L2, которое на рис.4 изображено через n. Записываем положение экрана n2 в делениях шкалы. Не двигая линзы L1 и L2 смещаем экран и опять добиваемся отчетливого изображения предмета на экране и записываем значение n2. Опыт повторяем 5 раз. Обработка результатов опыта. По полученным значениям n1, n, n2 вычисляют значения d и f. Воспользовавшись формулой (7), вычисляют фокусное расстояние рассеивающей линзы F2. По данным опыта вычисляют относительную погрешность определения F2, а затем и абсолютную погрешность. Обработка результатов. Таблица 1. Определение фокусного расстояния собирающей линзы.
Таблица 2. Определение фокусного расстояния собирающей линзы (метод Бесселя).
Таблица 3. Определение главного фокусного расстояния рассеивающей линзы.
Определение фокусного расстояния собирающей линзы.  мм мм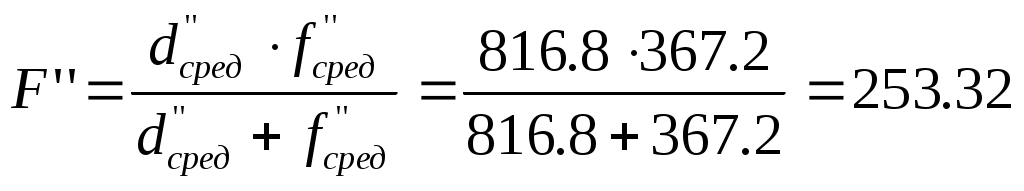 мм ммВычислим среднеквадратичные погрешности отдельных измерений: Принимаем Р=0,95 и по таблице найдем коэффициент Стьюдента для пяти измерений α=2,8. Вычислим случайные погрешности: Полная погрешность с учетом приборной: Вычислим относительную погрешность измерения F: Вычислим абсолютную погрешность измерения F: Запишем окончательный результат вычисления F: Определение фокусного расстояния собирающей линзы (метод Бесселя). Вычислим среднеквадратичные погрешности отдельных измерений: Принимаем Р=0,95 и по таблице найдем коэффициент Стьюдента для пяти измерений α=2,8. Вычислим случайные погрешности: Полная погрешность с учетом приборной: Вычислим относительную погрешность измерения F: Вычислим абсолютную погрешность измерения F: Запишем окончательный результат вычисления F: Считаем, что Вычислим радиус кривизны линзы: Определение главного фокусного расстояния рассеивающей линзы. Вычислим значение d и f: Вычислим фокусное расстояние рассеивающей линзы F2: Вычислим среднеквадратичные погрешности отдельных измерений: Принимаем Р=0,95 и по таблице найдем коэффициент Стьюдента для пяти измерений α=2,8. Вычислим случайные погрешности: Полная погрешность с учетом приборной: Вычислим погрешность: Вычислим относительную погрешность F2: 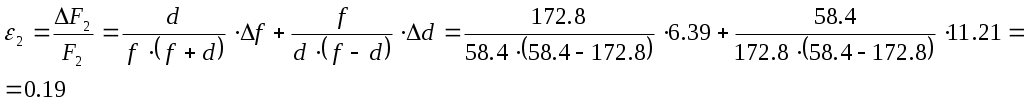 Вычислим абсолютную погрешность измерения F2: Вычислим абсолютную погрешность измерения F2:Запишем окончательный результат вычисления F2: |
