оооо. Лабораторная работа 1 определение концентрации и подвижности носителей тока у полупроводников с помощью эффекта холла цель работы
 Скачать 357 Kb.
|
|
Лабораторная работа №1 ОПРЕДЕЛЕНИЕ КОНЦЕНТРАЦИИ И ПОДВИЖНОСТИ НОСИТЕЛЕЙ ТОКА У ПОЛУПРОВОДНИКОВ С ПОМОЩЬЮ ЭФФЕКТА ХОЛЛА ЦЕЛЬ РАБОТЫ Эффект Холла относится к группе гальваномагнитных явлений и заключается в том, что под действием магнитного поля, перпен-дикулярного к электрическому току, электроны в материале откло-няются перпендикулярно как направлению электрического тока, так и магнитного поля. С помощью эффекта Холла стало возмож-ным понять суть процессов проводимости в полупроводниках и провести грань между полупроводниками и другими типами плохо проводящих материалов. Это обусловлено тем, что измерение ЭДС (разности потенциалов) Холла, возникающей в материале перпен-дикулярно направлению электрического тока и внешнего магнит-ного поля, дает возможность непосредственно определить концен-трацию и знак носителей заряда. Последнее позволяет определить принадлежность материала к тому или иному типу полупровод-ников (p или n–типа). Измерения эффекта Холла дают возможность отделить случай ионной проводимости от случая электронной про-водимости. Наличие эффекта Холла в проводниках и полупрово-дниках свидетельствует об электронном характере проводимости. С помощью эффекта Холла возможно получить данные и о под-вижности носителей заряда (так называемая «холловская» подвиж-ность). Таким образом, эффект Холла – один из наиболее эффек-тивных методов исследования электрических свойств полупровод-никовых материалов. Целью работы является изучение зависимости ЭДС Холла в по-лупроводниковом образце от величины магнитного поля и опреде-ление концентрации носителей заряда и некоторых других пара-метров. ОСНОВНЫЕ ПОЛОЖЕНИЯ ТЕОРИИ Наблюдение эффекта Холла сводится к измерению поперечной ЭДС, возникающей между узкими сторонами пластинки под дейст-вием магнитного поля. По сути это внешнее напряжение, необ-ходимое для того, чтобы электрический ток был направлен точно по оси, например, вдоль длины образца. Пусть образец имеет форму прямоугольной пластинки длиной  , шириной  , толщиной  (рис. 1). Если вдоль длины образца (ось 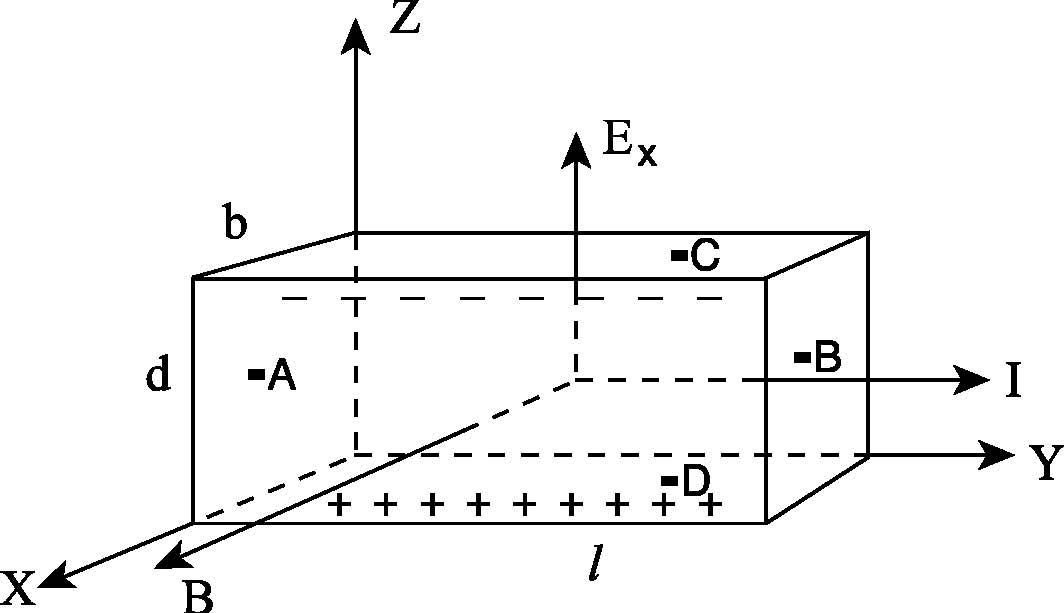 ) пропустить электрический ток  , вдоль оси  приложить магнитное поле  , то в направ-лении, перпендикулярном  и  (ось  ), возникает электрическое поле, называемое полем Холла с напряженностью  . Рис 1. Ориентация тока, индукции магнитного поля и напряжен-ности холловского поля в полупроводниковой пластине  –типа.На практике, как правило, поле Холла характеризуют разностью потенциалов, которую измеряют между симметричными точками С и D на боковых поверхностях образца. Эта разность потенциалов называется холловской разностью по-тенциалов  или ЭДС Холла. В классической теории проводи-мости эффект Холла объясняется тем, что в магнитном поле на движущиеся электрические заряды действует сила Лоренца, вели-чина и направление которой определяется векторным уравнением: , (1)где – индукция магнитного поля, – дрейфовая скорость движения зарядов, – заряд носителей тока с учетом знака, « » – для ды-рочной проводимости, « » – для электронной проводимости. Таким образом, дрейф электронов будет иметь составляющую не только по оси , но и по оси . При этом дрейф электронов вдоль оси будет продолжаться до тех пор, пока возникающее электри-ческое поле  не уравновесит силу Лоренца.Электрическое поле Холла  (2)связано с холловской разностью потенциалов  следующим образом:  (3)Сила тока, протекающего через единицу поверхности образца, т.е. плотность тока, равна:  , (4)где  – число носителей тока в единице объема образца (кон-центрация носителей тока), то сила тока , (5)что позволяет записать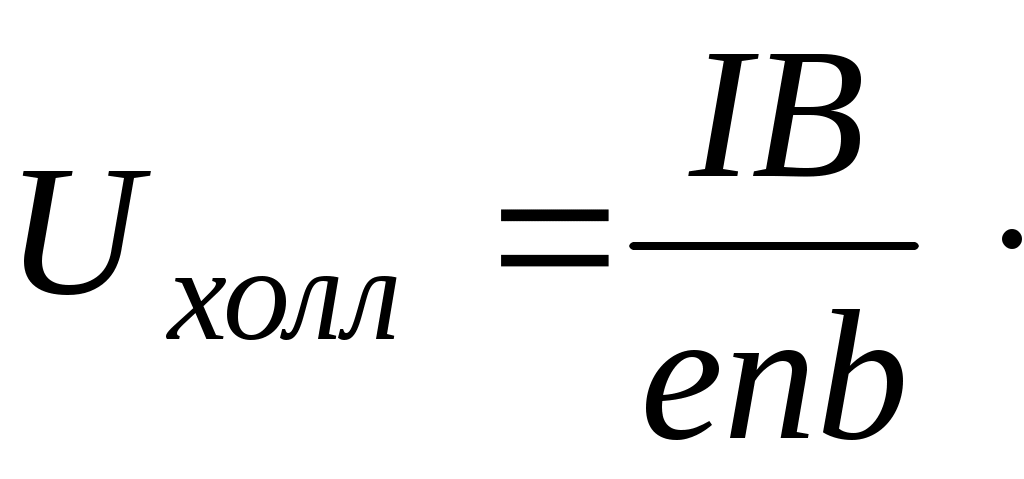:  (6)и  (7)Таким образом, ЭДС Холла пропорциональна силе тока через образец и обратно пропорциональна толщине образца . Экспериментальное определение ЭДС Холла проводят на образ-це с заданной толщиной  при фиксированном токе через образец. Формула (7) может быть записана в виде: , (8)где коэффициент пропорциональности  (9)является характеристикой изучаемого вещества и называется коэффициентом Холла или постоянной Холла. Из уравнения (9) видно, что коэффициент Холла обратно пропорционален концен-трации носителей заряда и его знак совпадает со знаком носителя заряда. Измеряя в ходе эксперимента разность потенциалов 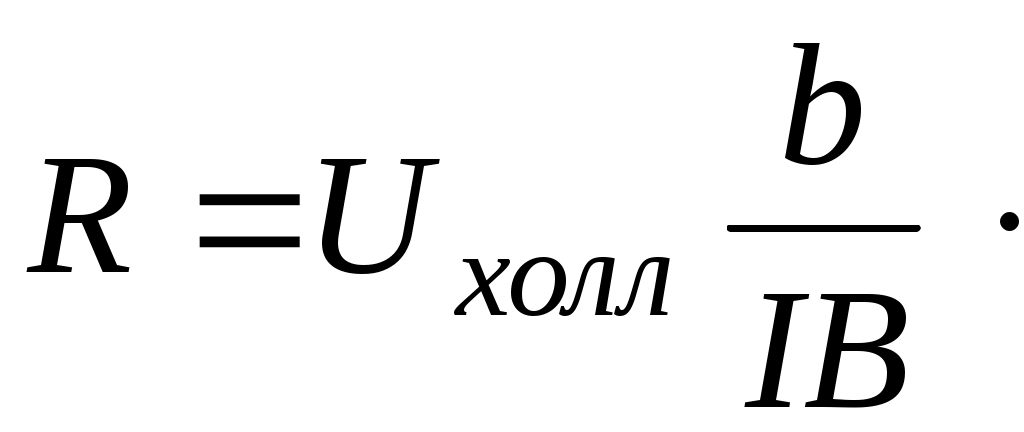 , индукцию магнитного поля , ток и толщину образца , можно, исходя из формулы (8), вычислить постоянную Холла: (10)Рассмотрим далее, как меняется знак в зависимости от зна-ка носителей заряда. На рис.2 проводящая пластина изображена в плоскости листа, магнитное поле направлено к нам, перпенди-кулярно листу, ток течет по стрелке.  а) б) Рис. 2. а) полупроводник n–типа, б) полупроводник p–типа Если носители тока – электроны, то направление их дрейфовой скорости будет противоположно направлению тока. При таком нап-равлении скорости в указанном магнитном поле на электрон будет действовать сила Лоренца, направленная вниз. Верхняя грань про-водящей пластины должна заряжаться положительно, а нижняя – отрицательно. На рис.2б видно, что в случае положительных носителей заряда (при том же направлении тока) меняется направление дрейфовой скорости зарядов, а направление силы Лоренца остается той же, т.е. в этом случае вниз будут отклоняться положительные заряды. Именно это и позволяет экспериментально определить знак носи-телей заряда в проводящей пластине. Направление поля Холла за-висит от знака носителей заряда. В нашем случае в полупро-водниковой пластине -типа поле Холла направлено вверх, а в случае полупроводника -типа – вниз. Таким образом, по знаку холловской разницы потенциалов определяется знак постоянной Холла и, соответственно, знак носителей заряда. Теперь, исходя из формулы (9), можно вычислить концентрацию носителей заряда в полупроводнике  , (11)где  Кл – заряд электрона. Рассмотренный эффект Холла, причиной которого является действие силы Лоренца на движущиеся в магнитном поле заряды, называется классическим эффектом Холла. Мы будем изучать эффект Холла в полупроводниках, поскольку в них эффект Холла имеет в основном классическую природу, и, следовательно, для его описания справедливо выражение (9). Вы-ражение (9) для классической постоянной Холла получено в пред-положении, что все носители тока имеют одинаковую дрейфовую скорость движения , которая не изменяется при движении носи-телей заряда в веществе. В действительности, необходимо учиты-вать механизм рассеяния носителей заряда в твердом теле, что не-избежно приведет к уточнению значения постоянной Холла. В об-щем случае  определяется следующим выражением: , (12)где  –Холл-фактор. С помощью Холл-фактора учитываются разные механизмы рас-сеяния носителей заряда. При рассеянии на тепловых колебаниях решетки расчет дает значение 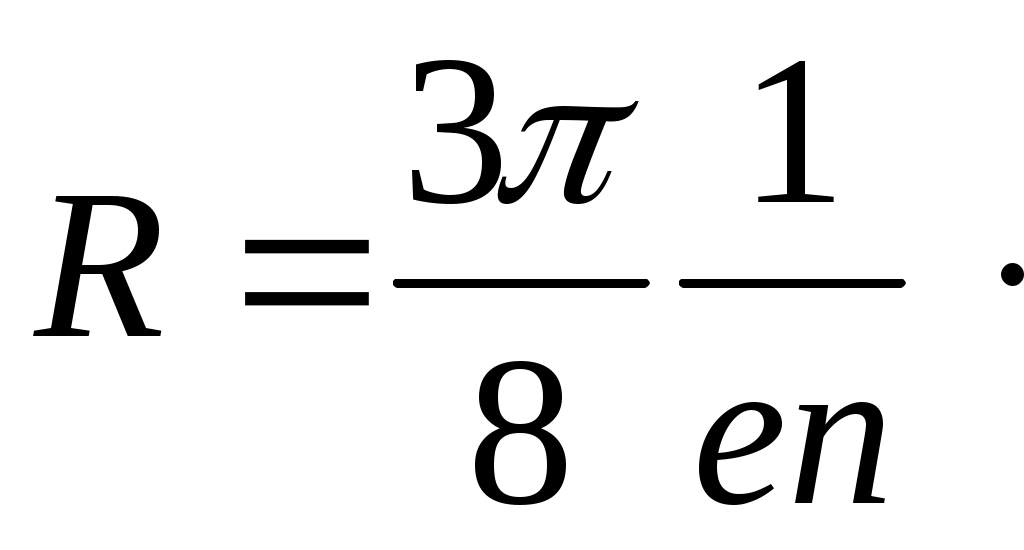 . Это случай собственных полупроводников и полупроводников, имеющих носители заряда одного знака. В случае вырожденных полупроводников и металлов  , а при преимущественном рассеянии на ионах примеси  ,. Таким образом, в чистых полупроводниках с собст-венной проводимостью преобладает рассеяние на колебаниях ре-шетки (например, в германии и кремнии при высоких и комнатных температурах), а для постоянной Холла получается выражение (13)Следует обратить внимание на то, что концентрация носителей заряда (как положительных – , так и отрицательных – ) сильно зависит в полупроводниках от температуры. Следовательно, и пос-тоянная Холла также зависит от температуры. В области собствен-ной проводимости  уменьшается по модулю с ростом темпера-туры. При экспериментальном определении следует обратить внимание на то, что наряду с эффектом Холла наблюдаются также некоторые другие эффекты: гальваномагнитный, термомагнитный эффекты и др. Для исключения влияния побочных эффектов ис-пользуют свойство четности этих эффектов, т.е. их независимость от направления магнитного поля. Между тем эффект Холла, явля-ясь нечетным эффектом, меняет свой знак при изменении направ-ления магнитного поля. Для того чтобы исключить побочные эффекты и определить ис-тинное значение 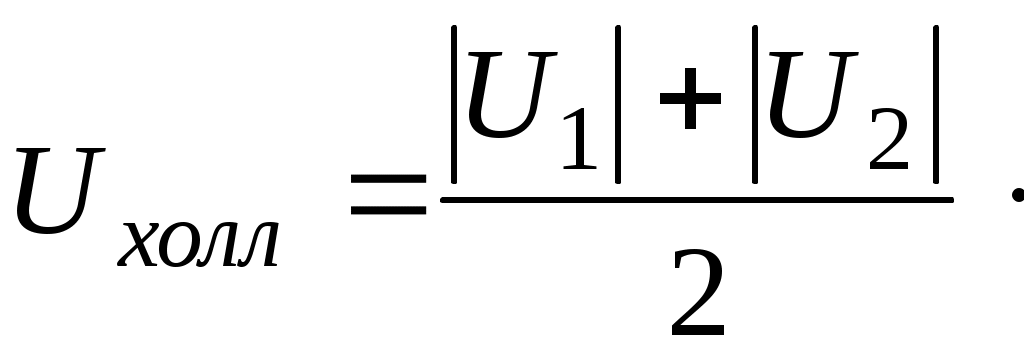, (для определения концентрации носителей заряда), напряжение между холловскими контактами измеряют при двух направлениях магнитного поля. Действительно, пусть при вы-бранном направлении поля напряжение между холловскими кон-тактами  ; при изменении направления поля на про-тивоположное напряжение  . Отсюда:  (14)Таким образом,  , обусловленное побочными четными эф-фектами, исключено.Если наряду с постоянной Холла определить удельное сопро-тивление полупроводника, то можно вычислить еще такую важную характеристику, как подвижность носителей заряда. Подвижностью носителей заряда  называется дрейфовая ско-рость носителей заряда, которую они приобретают в электрическом поле с напряженностью 1 В/м. Очевидно, что если носители заряда движутся в поле с напря-женностью  , то их дрейфовая скорость:  . (15)Если концентрация носителей заряда – , заряд –  , то плот-ность электрического тока через образец равна . (16)По закону Ома  , (17)где  – удельная электропроводность вещества (проводимость), которая согласно (16) и (17) выражается через подвижность форму-лой:  , (18)тогда удельное электрическое сопротивление:  , (19)отку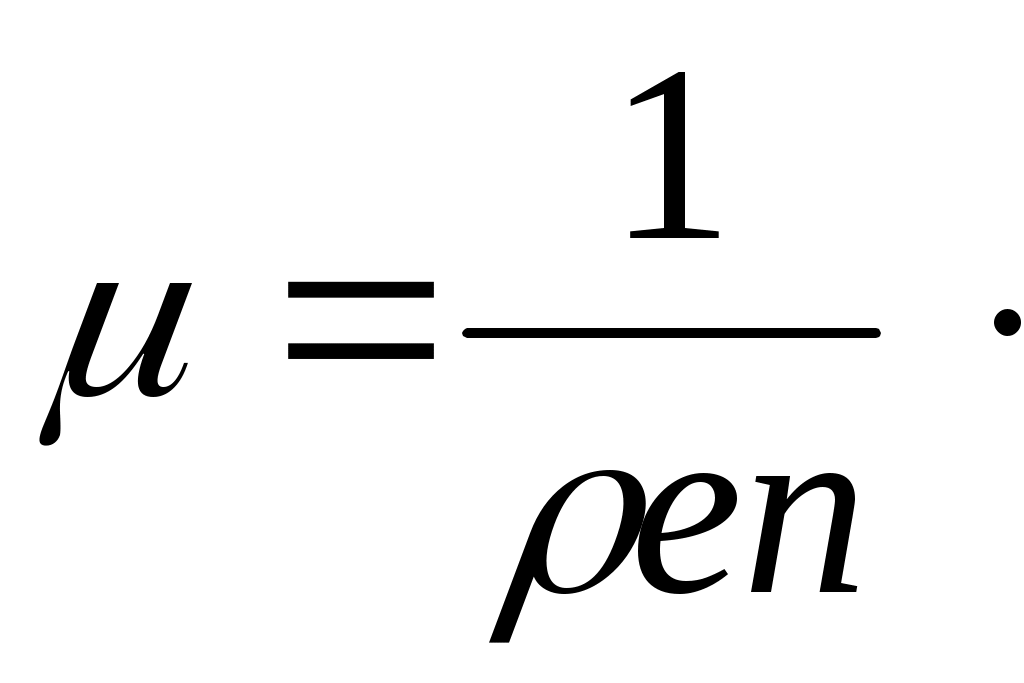да:  (20)С учетом выражения (13) для постоянной Холла ( 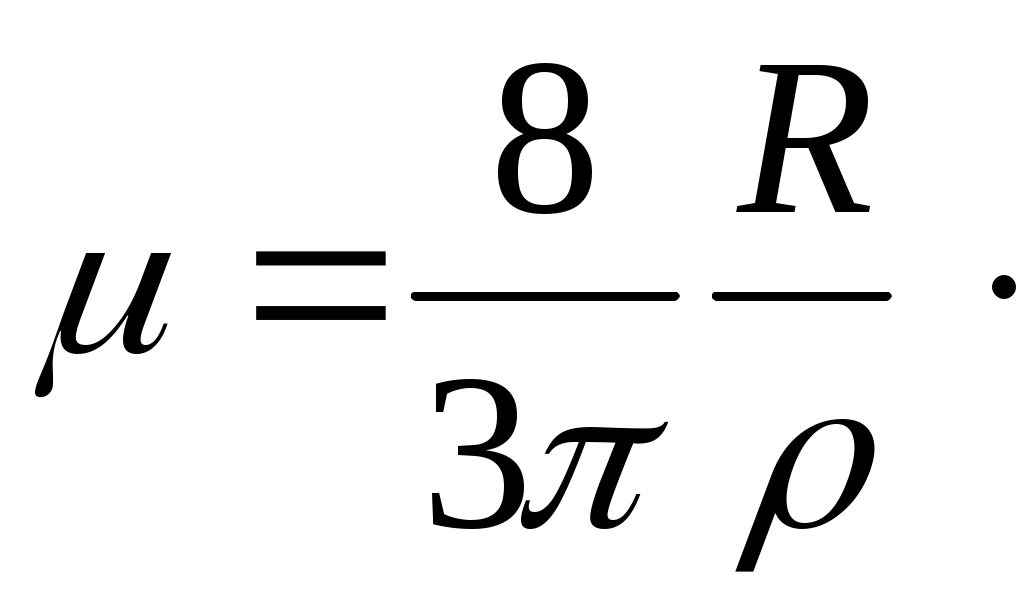), подвиж-ность носителей заряда выражается следующим образом:  (21) Подвижность, которая определяется с помощью эффекта Холла, называется «холловской» подвижностью носителей заряда, в отли-чие от дрейфовой подвижности. В области собственной проводи-мости (  ) обычно подвижность электронов ( ) больше подвиж-ности дырок ( ), поэтому в собственных полупроводниках  . Если же  , то  и  . Это означает, что отклоняе-мые в одну и ту же сторону электроны и дырки не создают поля Холла (их заряды компенсируют друг друга, и поле не возникает). В случае, когда  и  , знак определяется знаком но-сителей заряда, которые имеют большую подвижность. Для определения удельного электрического сопротивления изу-чаемого полупроводника измеряют электрическое сопротивление между двумя контактами (А и В на рис.1), расположенными на длинной поверхности образца на расстоянии  . С этой целью про-пускают электрический ток вдоль длины образца и измеряют па-дение напряжения  между указанными контактами. Тогда удель-ное сопротивление вычисляется по формуле:  ,где  – поперечное сечение образца. ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ 1. Включить установку. Дать прогреться приборам 10 минут. 2. С помощью регулятора «Установка тока датчика Холла» уста-новить ток датчика 0,5–1,5 мА (по указанию преподавателя). 3. Произвести установку нуля микровольтметра. Для этого: – установить переключатель S1 в положение «2», при этом цепь питания соленоида разрывается, то есть ток соленоида равен нулю (убедиться в этом по показанию прибора). – с помощью регулятора микровольтметра «Установка нуля» уста-новить нуль микровольтметра, измеряющего ЭДС Холла (при этом возможен дрейф младшего разряда прибора). 4. Перевести переключатель S1 в положение «1», установить ток соленоида 2,0–2,5 мА. 5. Измерить ЭДС Холла с помощью микровольтметра. Результат измерения  записать в таблицу 1. 6. Перевести переключатель S1 в положение «3», при этом ток потечет в противоположном направлении. Вновь произвести изме-рение ЭДС Холла. Результат измерения  записать в таблицу 1.Таблица 1
Примечание:  – значения ЭДС Холла для противоположно направленных токов соленоида. Величина вычисляется по формуле (14). 7. Увеличить ток через соленоид на 1,5–2,0 мА и произвести из-мерение ЭДС Холла по пунктам 5,6. Всего произвести 8–10 изме-рений ЭДС Холла, увеличивая при каждом новом измерении ток через соленоид на 1,5–2,0 мА. Последнее измерение произвести при токе соленоида 10–15 мА. ОБРАБОТКА РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ 1. Построить график зависимости ЭДС Холла от тока соленоида и провести по экспериментальным точкам прямую линию, выража-ющую зависимость:  , (22)учитывая, что точка (0,0) является результатом измерений, пря-мая должна проходить через начало координат. 2. Вычислить из графика постоянную  :  , (23)где  – тангенс угла наклона прямой на графике.3. Вычислить постоянную Холла по формуле:  , (24)где – толщина германиевой пластинки в датчике; Гн/м – магнитная постоянная; – число витков на единицу длины соленоида; – ток датчика Холла. Для Л.Р.№ 421, 422:  вит/м;  мм.Для Л.Р.№ 423: вит/м;  мм.4. По формулам (11) и (13) вычислить концентрацию носителей за-ряда в полупроводнике германия. 5. Вычислить по формуле (13) концентрацию носителей заряда и по формуле (21) подвижность носителей заряда для кремния – типа (примесь – фосфор) с удельным сопротивлением   и известным значением постоянной Холла   и для образца кремния – типа (примесь – бор) с удельным сопротив-лением  и  . КОНТРОЛЬНЫЕ ВОПРОСЫ 1. В чём состоит эффект Холла? 2. Какова природа носителей тока в полупроводниках? 3. Как создаются полупроводники –типа и –типа?4. Что такое дрейфовая скорость носителей тока? 5. Как определяется физическая величина, называемая «подвиж-ность носителей тока»? 6. Что такое собственная проводимость и примесная проводи-мость полупроводников? 7. Коэффициент Холла у полупроводников на несколько поряд-ков больше, чем у металлов. Чем это объясняется? 8. При измерении эффекта Холла в некотором полупроводнике оказалось, что полярность холловской разности потенциалов про-тивоположна той, которая наблюдалась у медной пластинки. Как это можно объяснить? 9. Можно ли по измеренной постоянной Холла (не имея другой информации о данном образце) определить концентрацию носи-телей тока в примесном полупроводнике? 10. В чём состоит главная причина того, что электрическая про-водимость металлов на несколько порядков больше, чем у полупро-водников? 11. В некотором образце измерили холловскую разность потен-циалов Uхолл при токе через образец, равном I. Как изменится Uхолл, если образец по ширине d (см. рис.1) уменьшить вдвое, а плот-ность тока в образце оставить прежней? 12. Как изменится холловская разность потенциалов Uхолл, если толщину образца уменьшить вдвое, а плотность тока оставить прежней? 13. Как изменится холловская разность потенциалов Uхолл, если все геометрические размеры образца (длина, ширина, толщина) уменьшить вдвое, а ток через образец оставить прежним? 14. Наблюдается ли эффект Холла в собственных полупроводни-ках? 15. Зависит ли эффект Холла от температуры? 16. В аналоговых ЭВМ эффект Холла используется для умно-жения двух сигналов. На вход устройства подаются два тока I1 и I2, а на выходе получается сигнал, пропорциональный произведению токов: (I1·I2). Как это можно сделать, используя эффект Холла? 17. Чувствительность датчиков Холла 0,1 В/Тл. Можно ли с помощью датчика Холла измерить индукцию магнитного поля Зем-ли? 18. Почему для измерения эффекта Холла используется изме-рение ЭДС Холла, а не тока? 19. При установке датчика Холла внутрь соленоида датчик слу-чайно сместился и плоскость пластинки оказалась наклонённой к оси соленоида на угол 70.Как это скажется на измерении ЭДС Холла? 20. При установке датчика Холла внутрь соленоида датчик слу-чайно сместился и оказался точно на краю соленоида. Как это ска-жется на измерении ЭДС Холла? 21. При увеличении тока через датчик пропорционально току увеличивается ЭДС Холла. Сохраняется ли эта зависимость при большом токе? 22. Чем ограничивается увеличение тока через датчик Холла? 23. Как исказятся результаты измерений, если ток в датчике Холла превысит максимальное значение, указанное в паспорте на датчик? 24. Как должна быть установлена поверхность пластины дат-чика Холла относительно оси соленоида? 25. Напряжение Холла при одном и том же значении тока соле-ноида измеряется дважды: при одном направлении тока и при из-менении тока на противоположное. Зачем это нужно? 26. Датчик Холла не выдаёт ЭДС, но все электрические кон-такты в порядке. В чём может быть причина неисправности и как её устранить? 27. Что можно сделать для увеличения чувствительности при-обретённого (т.е. уже изготовленного) датчика Холла? 28. В паспорте на один из типов датчиков Холла (ДХГ–2) указан интервал температур, в котором может работать датчик. Минимальная температура для этого датчика – минус 60. Чем объясняется такое ограничение температуры? 29. Будет ли наблюдаться эффект Холла у датчика ДХГ-2 (см. предыдущий вопрос) при температуре ниже –60. 30. При подключении датчика Холла были перепутаны кон-такты: к контактам для пропускания тока подключили измеритель ЭДС Холла, а контактом, предназначенным для измерения ЭДС, подключили источник тока. Будет ли наблюдаться эффект Холла в этом случае? |
,
,