Лабораторная работа 1-3. Теория и образец выполнения. Лабораторная работа 1 Первичная обработка статистических данных

• Название: Лабораторная работа 1 Первичная обработка статистических данных
• Дата: 28.03.2023
• Размер: 0.75 Mb.
• Имя файла: Лабораторная работа 1-3. Теория и образец выполнения.doc
• Тип: Лабораторная работа; #1022449
• страница: 3 из 3

тогда

(2.19)

где границы частичных интервалов;

длина частичных интервалов.

Получаем, что все равны одному числу .

3. Составить сводную таблицу на основе эмпирических вероятностей и рассчитанных теоретических вероятностей (см. табл. 2.6).

4. Оценку отклонения эмпирических вероятностей от теоретических вероятностей произвести с помощью критерия Пирсона (формула (2.14)).

5. По таблице критических точек распределения по заданному уровню значимости и по числу степеней свободы ( количество подынтервалов, - число параметров распределений, ) найти критические значения правосторонней критической области.

Далее анализируем в соответствии с правилами 2.1 и 2.2 (см. Гипотезу А).

Замечание 2.1. После составления таблицы 5 необходимо сделать на одном рисунке два графика: ломаную эмпирических вероятностей и кривую теоретических вероятностей.

Замечание 2.2. Здесь же на этом рисунке рекомендуется нанести:

а) ; б) доверительный интервал, построенный для одной из доверительных вероятностей (например, для ); в) интервал, построенный по правилу «3-х сигм».

Замечание 2.3. Данный рисунок является наглядным результатом работы, проделанной в Л.Р. 1,2,3.

ПРИМЕР 2.3. Используя критерий согласия Пирсона при уровне значимости , проверить гипотезу о нормальном распределении генеральной совокупности.

1) Переносим из лабораторной работы № 1 полигон распределения относительных частот и табл. 2.5.

	130,6	290	449,3	608,6	768	927,3	1086,6	1246	1405
	0,06	0,14	0,25	0,18	0,16	0,1	0,05	0,03	0,03

2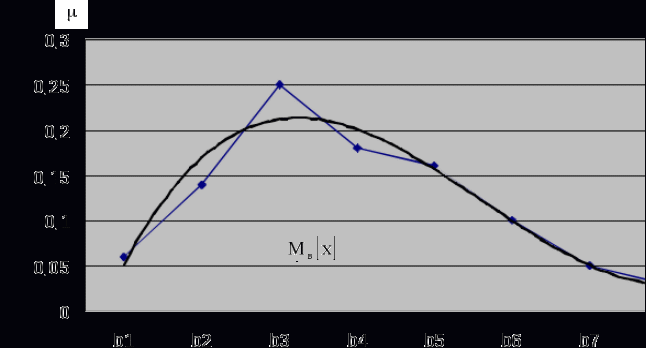


) Из визуального наблюдения ломаной делаем предположение (ставим гипотезу) о законе распределения генеральной совокупности, то есть ставим гипотезу : выборка распределена по нормальному закону.

3) Вычислим теоретические вероятности 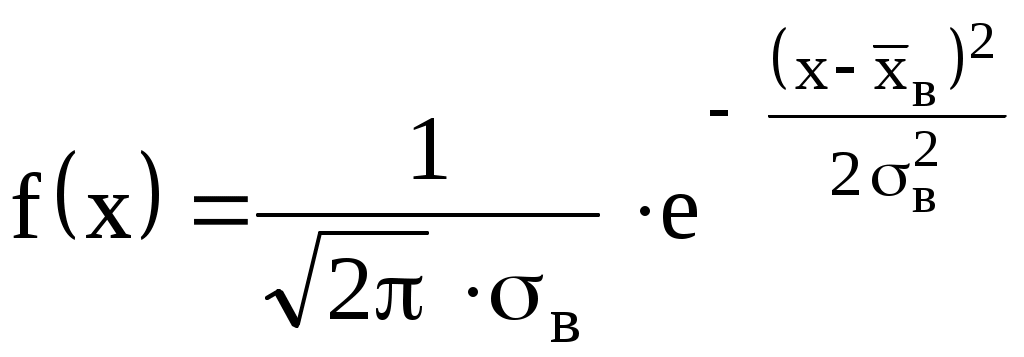. Для этого записываем функцию плотности для нормального закона:

.

Соответственно 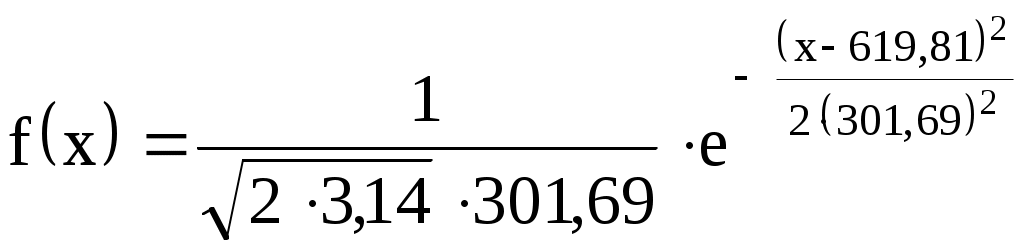или

.

Тогда .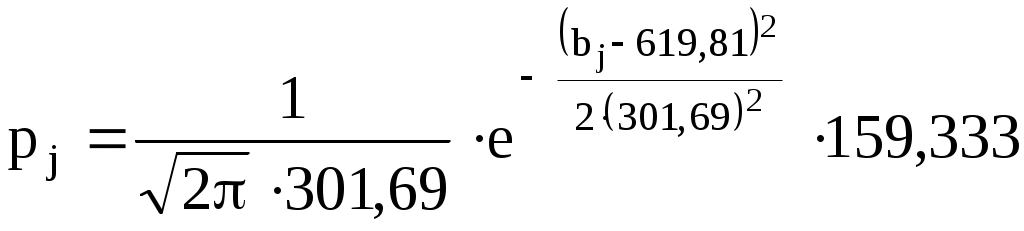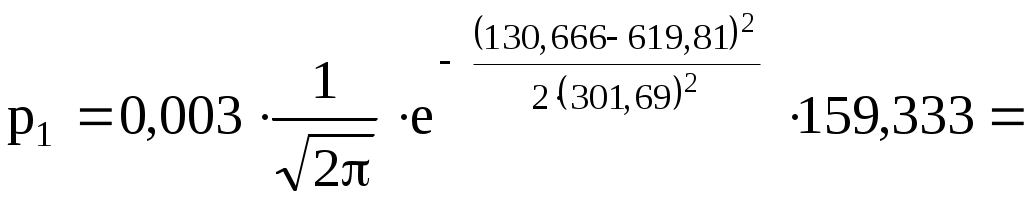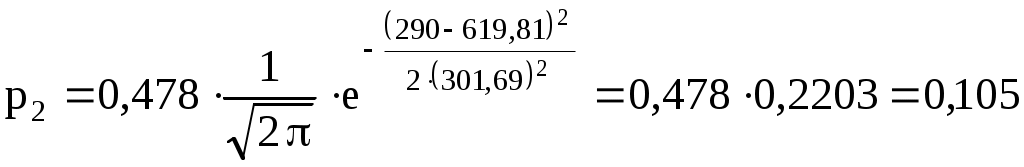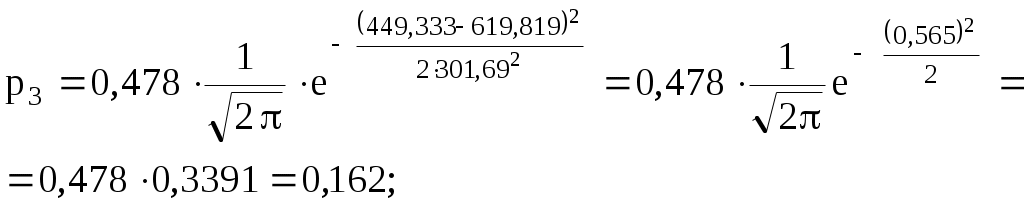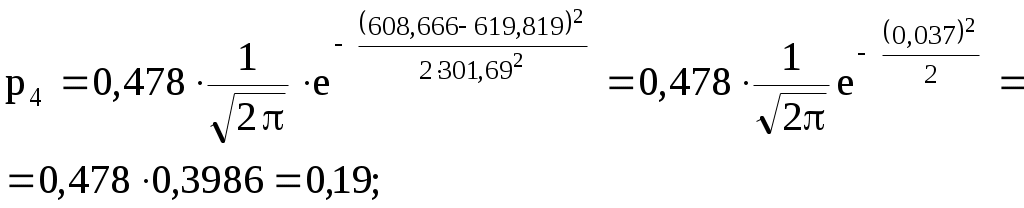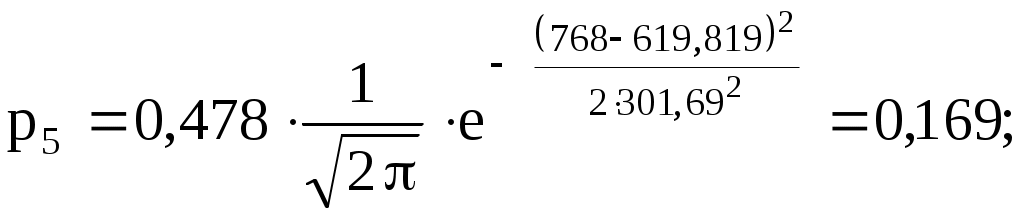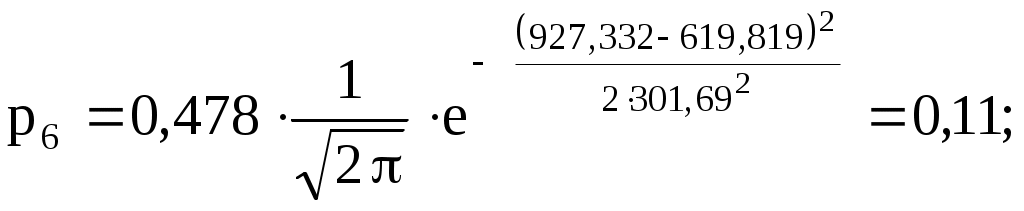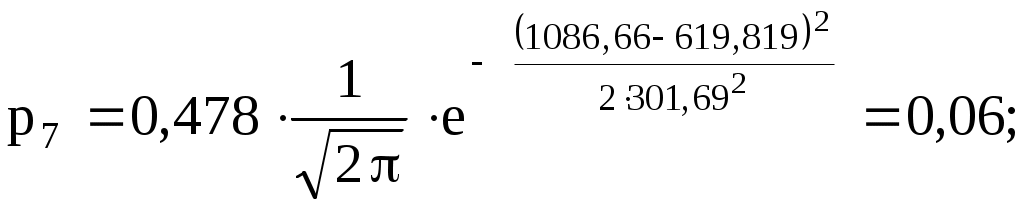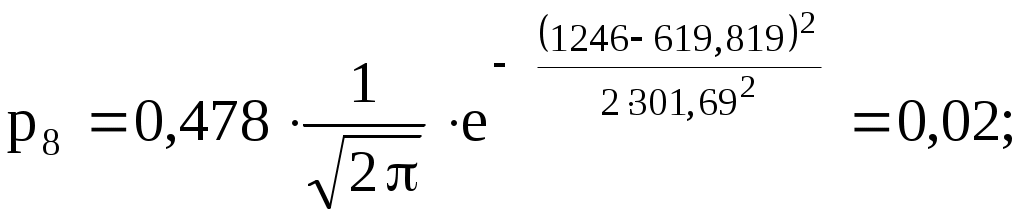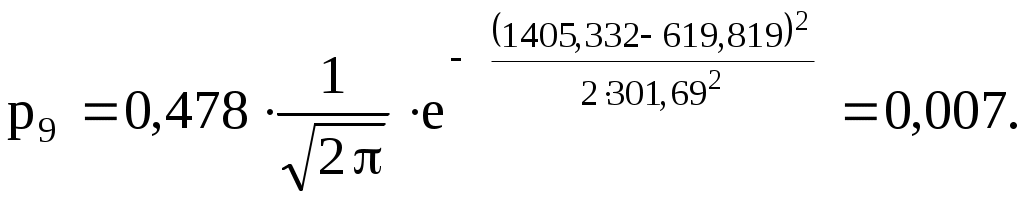

;

;















4) Составляем табл. 2.7 распределения теоретических вероятностей.

Таблица 2.7

	130,6	290	449,3	608,6	768	927,3	1086,6	1246	1405
	0,06	0,14	0,25	0,18	0,16	0,1	0,05	0,03	0,03
	0,05	0,105	0,162	0,19	0,17	0,11	0,06	0,02	0,007

Отметим теоретические вероятности на полигоне относительных частот.

5) Рассчитаем значение критерия .

.

6) Из таблицы «Критические точки распределения » находим соответствующее нашим значениям .



. .

Сравниваем и . Так как , то гипотеза (выборка распределена по нормальному закону) принимается, по правилу 2.1.