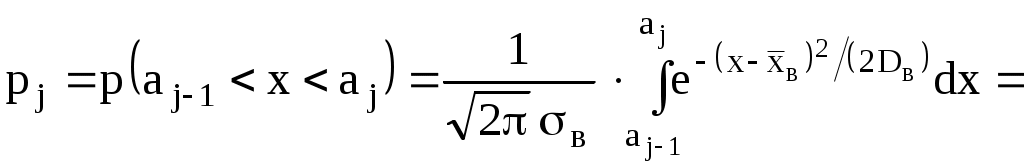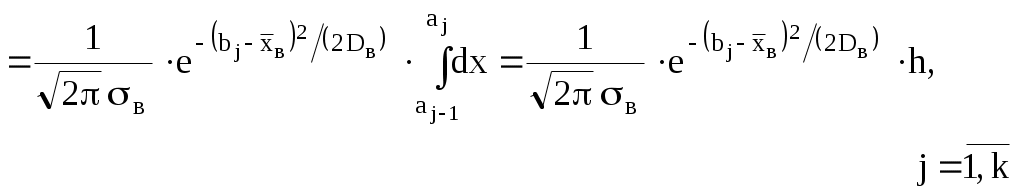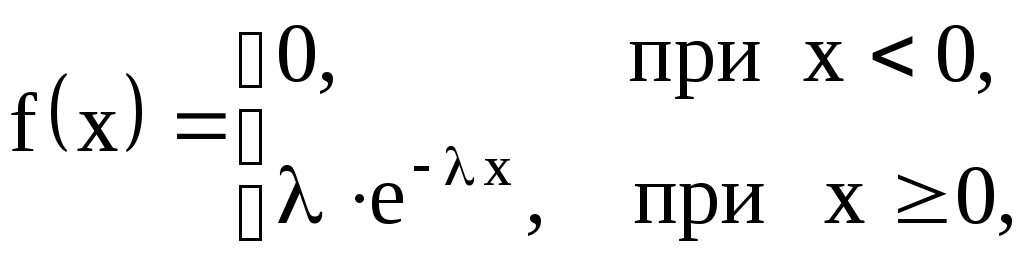Лабораторная работа 1-3. Теория и образец выполнения. Лабораторная работа 1 Первичная обработка статистических данных

• Название: Лабораторная работа 1 Первичная обработка статистических данных
• Дата: 28.03.2023
• Размер: 0.75 Mb.
• Имя файла: Лабораторная работа 1-3. Теория и образец выполнения.doc
• Тип: Лабораторная работа; #1022449
• страница: 2 из 3

ПРИМЕР 2.2. Найти точечные и интервальные оценки генерального математического ожидания и генеральной дисперсии, исходя из данных примера 2.1.

1) По данным таблицы 2.5 рассчитываем выборочное математическое ожидание и выборочную дисперсию, среднее квадратическое отклонение.











.

.

По данным табл. 2.4 вычисляем еще одну точечную характеристику среднее арифметическое значение нашей выборки : .

2) Делаем расчет интервальных оценок, то есть будем строить доверительные интервалы с доверительной вероятностью .

а)

Ищем соответствующее значение по таблице в приложении 2 .

Точность оценки . Тогда

;

.

б)

.

;

.

Строим полученные интервалы на полигоне распределения относительных частот.

2


.3 Лабораторная работа № 3

«Проверка гипотезы о законе распределения генеральной совокупности».
В лабораторной работе №1 в результате первичной обработки исходных данных получено эмпирическое распределение (табл. 2.3) и по данным этой таблицы построен полигон относительных частот. Относительные частоты иногда называют эмпирическими вероятностями. Из визуального наблюдения полигона можно сделать один из следующих выводов:

Гипотеза : Генеральная совокупность распределена по нормальному закону;

Гипотеза : Генеральная совокупность распределена по

показательному закону;

Гипотеза : Генеральная совокупность распределена по равномерному закону.

Гипотеза .

Для того, чтобы при заданном уровне значимости ( доверительная вероятность, то есть вероятность принять верную гипотезу; это вероятность отвергнуть верную гипотезу ), проверить гипотезу о нормальном распределении генеральной совокупности надо:

1. Вычислить (лабораторная работа № 2).

2. Вычислить теоретические вероятности . Поскольку плотность распределения для нормального закона есть

.

(2.12)

Тогда

	(2.13)

где границы частичных интервалов;

середина го частичного интервала;

длина частичного интервала (см. формулу (2.2)).

3. Составить сводную таблицу на основе данных табл. 2.3 и рассчитанных теоретических вероятностей:

Таблица 2.6

			…		…
			…		…		эмпирические вероятности
			…		…		теоретические вероятности

4. Оценку отклонения эмпирических вероятностей от теоретических вероятностей произвести с помощью критерия Пирсона :

.

(2.14)

5. По таблице критических точек распределения (приложение 4) по заданному уровню значимости и числу степеней свободы ( количество подынтервалов, - число параметров распределения, ) найти критическое значение правосторонней критической области.

Правило 2.1. Если , тогда нет оснований отвергать гипотезу о нормальном распределении генеральной совокупности (то есть эмпирические и теоретические частоты различаются незначимо (случайно).

Правило 2.2. Если , тогда гипотезу отвергаем.
Гипотеза .

Для того, чтобы при заданном уровне значимости , проверить гипотезу о показательном распределении генеральной совокупности надо:

1. Вычислить (лабораторная работа № 1). Принять в качестве оценки параметра показательного распределения величину, обратную выборочной средней:

.

(2.15)

2. Вычислить теоретические вероятности . Поскольку плотность распределения для показательного (экспоненциального) закона есть

(2.16)

тогда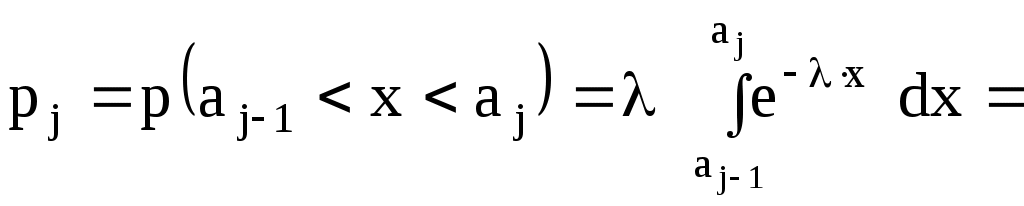



,

где границы частичных интервалов;

вычисляем по формуле (2.15).

3. Составить сводную таблицу на основе данных табл. 2.3 и рассчитанных теоретических вероятностей (см. табл. 2.6).

4. Оценку отклонения эмпирических вероятностей от теоретических вероятностей произвести с помощью критерия Пирсона (формула (2.14)).

5. По таблице критических точек распределения по заданному уровню значимости и по числу степеней свободы ( количество подынтервалов, - число параметров распределения, ) найти критическое значение правосторонней критической области (см. Приложение 4).

Далее необходимо проанализировать в соответствии с правилами 2.1 и 2.2 (для предыдущей гипотезы).

Гипотеза .

Для того, чтобы при заданном уровне значимости , проверить гипотезу о равномерном распределении генеральной совокупности надо:

1. Оценить параметры и концы интервала, в котором наблюдались возможные значения , по формулам (через и обозначены оценки параметров):

.

(2.17)

2. Вычислить теоретические частоты . Поскольку плотность распределения для равномерного закона есть

,

(2.18)