Аминев.ФФ лаба 4 тервер. Математическая статистика

Название	Математическая статистика
Дата	15.01.2022
Размер	184.45 Kb.
Формат файла
Имя файла	Аминев.ФФ лаба 4 тервер.docx
Тип	Лабораторная работа #331709

ФБГОУ ВО УФИМСКИЙ ГОСУДАРСТВЕННЫЙ АВИАЦИОННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

Лабораторная работа №4 на тему

«Математическая статистика»

Выполнил

студент гр. ИВТ-224

Аминев Ф.Ф
Проверил доц. каф. ВМиК

Гаянова М.М.

УФА-2021

Задание 1.

Найти точечные оценки математического ожидания, дисперсии, стандартного отклонения, а также стандартную ошибку математического ожидания:

а) по данным малой выборки (n=20);
б) по данным большой выборки (n=40);

Результаты представлены на рисунке 1.

Рисунок 1.

Задание 2.

Найти доверительные интервалы, соответствующие доверительные вероятности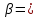

0,95

а) без использования MSExcel

Доверительный интервал для математического ожидания при малой выборки вычисляем по формуле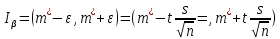

.

Число степ. свободы: n – 1 = 19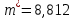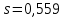

По таблице функции Лапласа найдемt: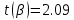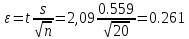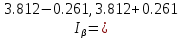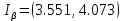

Доверительный интервал для математического ожидания при большей выборке вычисляем по формуле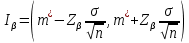

.

Число степ. Свободы: n – 1 = 39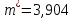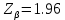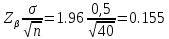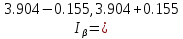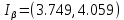

б) с использованием MSExcel

Результаты представлены на рисунке 2.

Рисунок 2.
Результаты выполнения заданий 2.2 и 2.3 представлены на рисунке 3.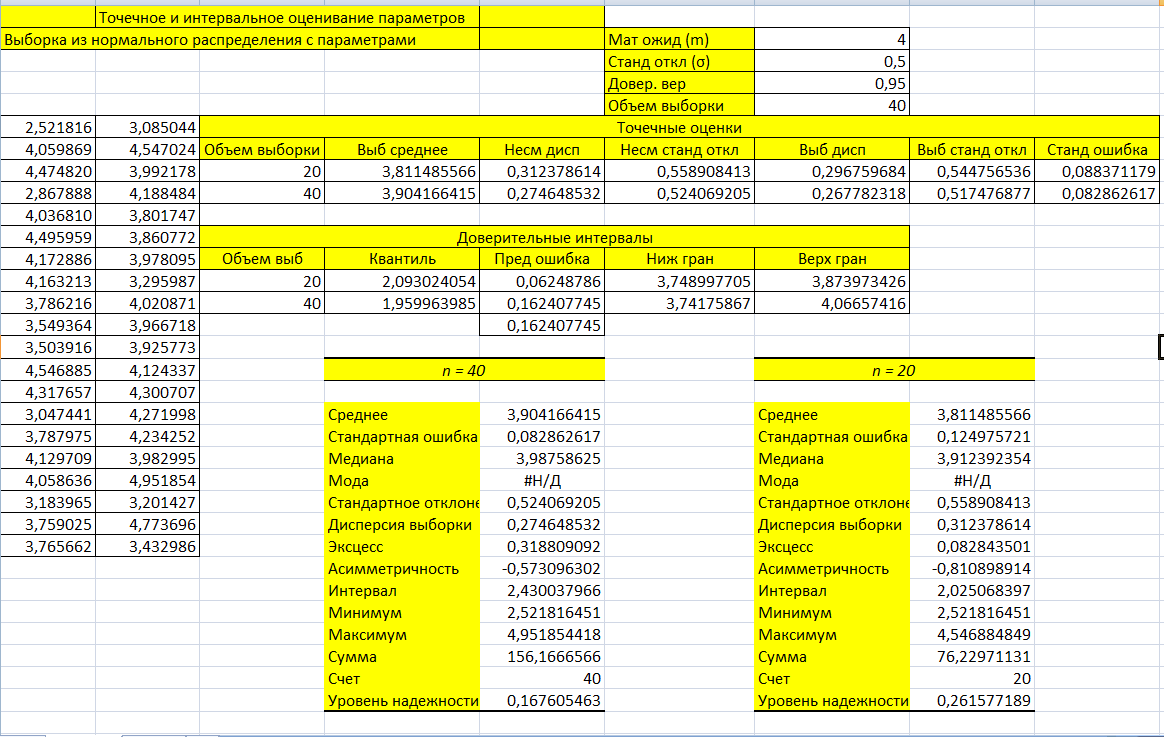

Рисунок 3.

Задание 3.

Выполнить с использованием MSExcel точечное и интервальное оценивание математического ожидания генеральной совокупности по данным выборки. Значение доверительной вероятности возьмите равным 0,90.

Таблица 1.

Последняя цифра шифра	0	1	2	3	4	5	6	7	8	9
m, σ	1; 0,4	1; 0,5	2; 0,5	2; 0,4	3; 0,5	3; 0,6	5; 0,6	6; 0,7	7; 0,6	8; 0,7
n	42	44	46	48	50	49	47	45	43	41

Результаты представлены на рисунке 4.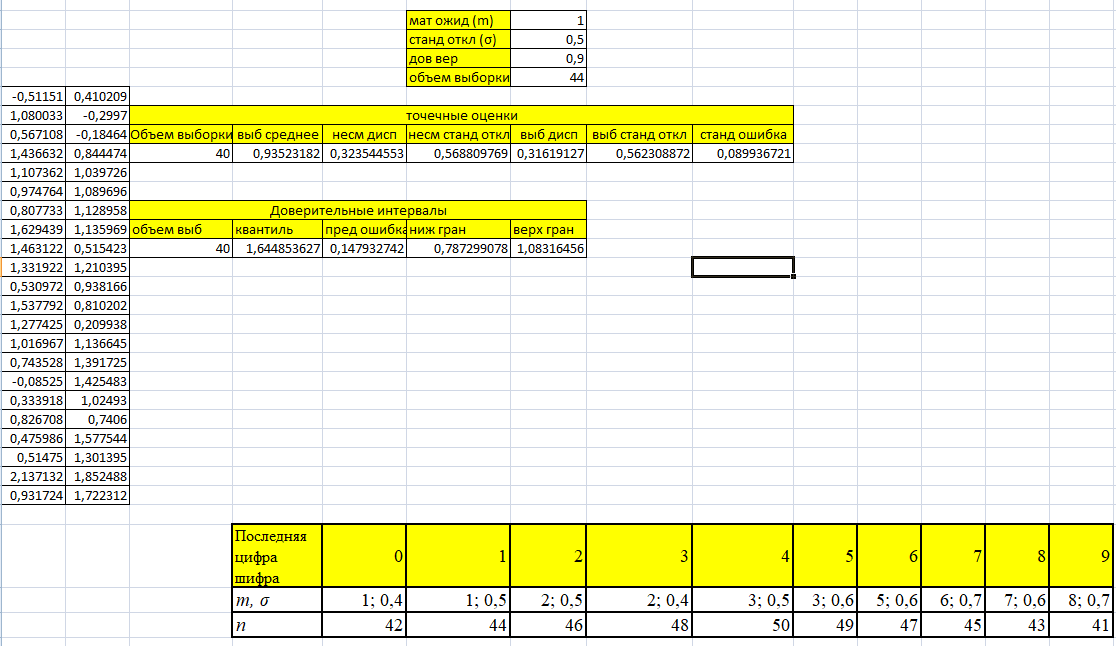

Рисунок 4.
Задание 4.

По результатам выполнения заданий 1 и 2 сформулировать и обосновать выводы о том, как изменяется точность найденных параметров в зависимости от объема выборки.

При увеличении числа выборки увеличивается точность оценок. Стандартное отклонение, дисперсия (несмещенная и выборочная), стандартная ошибка и предельная ошибка будут уменьшаться так как происходит повышение точности, что и ведёт к повышению точности оценки выборки.

При этом уменьшается нижняя граница и увеличивается верхняя, что свидетельствует о сужении интервала и к увеличению точности математического ожидания.