Лабораторная 1в18. Лабораторная работа 1 по дисциплине Дискретная математика
 Скачать 412.71 Kb. Скачать 412.71 Kb.
|
1 2 Задание 5.С помощью алгоритма Магу – Вейсмана выполнить правильную раскраску вершин графа с минимальным количеством цветов. Решение: Шаг 1. Для графа L = (X,U; P) общего вида построить его скелет. 1 3 2   7 8 6 4 5     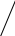   Шаг 2. Построить матрицу инциденций A графа L = (X,U) с элементами aij, где i = 1, n, j = 1,m, n = SXS — число вершин и m = SUS — число рёбер в графе L = (X,U).
Шаг 3. Ввести систему логических переменных x1, x2, . . ., xi , . . ., xn, подчинив её условиям, вытекающим из законов булевой алгебры: x2i = xi, xi + 1 = 1, а также законам коммутативности, ассоциативности и дистрибутивности. Шаг 4. Матрицу инциденций A преобразовать в матрицу Ax
и составить произведение 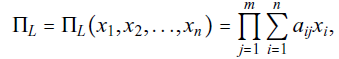 где j-й сомножитель произведения ΠL есть сумма двух слагаемых, соответствующих тем двум вершинам, которые в графе L соединены j-м ребром. ΠL = (x1+x2)*(x2+x3)*(x1+x5)*(x2+x5)*(x3+x5)*(x3+x6)*(x4+x5)*(x5+x6)* *(x5+x7)*(x5+x8)*(x7+x8) Шаг 5. Преобразовать выражение произведения ΠL к бесскобочному виду и при- вести его к минимальной форме, применяя законы дистрибутивности, ассоциативности, коммутативности и закон поглощения: а) a + a ⋅ b = a; б) (a + b)(a + c). . .(a + p) = a + b ⋅ c. . .p, где a, b, c, . . ., p — логические переменные, принимающие значения 0; 1, выполняя при этом условия, описанные в шаге 3. В результате выполненных преобразований выражение ΠL будет иметь минимальную форму и представлять выражение суммы произведений переменных из множества x1, x2, . . ., xi, . . ., xn, т. е. многочлен. Обозначим его ΣL. ΣL= x1x3x5x7 + x1x3x5x8 + x2x3x5x7 + x2x3x5x8 + x2x5x6x7 + x2x5x6x8 + +x1x2x3x4x6x7x8 Шаг 6. Для каждого слагаемого многочлена ΣLвыделить переменные, которые в него не входят, но входят в множество {x1, x2, . . ., xi, . . ., xn}. Эти переменные порождают максимальные пустые подграфы данного графа L, так как соответствующие им вершины в графе L образуют максимальные пустые подграфы.Упорядочить все максимальные пустые подмножества X1,X2,X3, . . .,Xi, . . ., Xk x2x4x6x8; x2x4x6x7; x1x4x6x8; x1x4x6x7; x1x3x4x8; x1x3x4x7; x5; Шаг 7. графа G в порядке возрастания их кардинальных чисел — │Xi│.Выбрать подмножество Xi, имеющее наибольшее значение кардинального числа — max │Xi│. max │Xi│= x2x4x6x8 Шаг 8. Присвоить цвет (допустим, синий) всем вершинам xt ∈ maxXi.  Шаг 9. Вычеркнуть из других подмножеств вершины, которым присвоен цвет. x7; x1; x1x7; x1x3; x1x3x7; x5; Выбрать подмножество Xi, имеющее наибольшее значение кардинального числа — max │Xi│. max │Xi│= x1x3x7, присвоить указанным вершинам цвет  Припишем оставшейся вершине множества x5 цвет  Ответ: хроматическое число γ(G) графа G равно трем: γ(G) = 3. Задание 6.Определить число вершинного покрытия графа (рис. 1). Вершинное покрытие – это такое множество S вершин графа, что у каждого ребра графа хотя бы один конец входит в S. Найдем минимальное вершинное покрытие.  Выбираем случайное ребро u6 . Добавляем в S обе его вершины: S={x2,x3}.Удаляем все ребра инцидентные x2,x3 .  Выбираем ребро u16. Добавляем в S его вершины: S={x2,x3 ,x7,x8} Удаляем все ребра инцидентные x7,x8 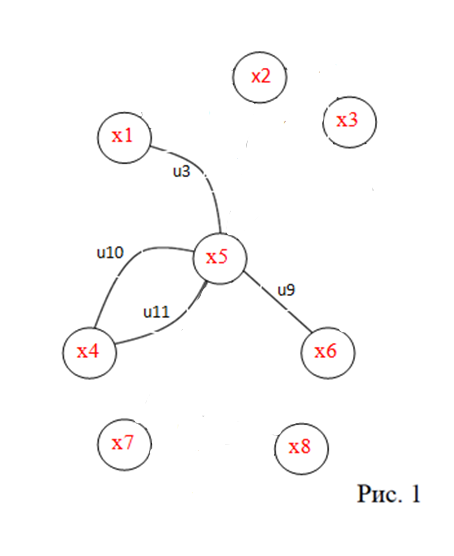 3. Выберем ребро u9 . Добавляем в S его вершины: S={x2,x3 ,x7,x8,x5,x6}. Удаляем все ребра инцидентные x7,x8  Получим вершинное покрытие S={x2,x3 ,x7,x8,x5,x6} Ответ: S={x2,x3 ,x7,x8,x5,x6} Число вершинного покрытия равно 6. Задание 7. Определить, содержит ли граф (рис. 1) эйлерову цепь или эйлеров цикл. Ответ обосновать.  Решение: Теорема. Для того, чтобы связный граф G был эйлеровым, необходимо и достаточно, чтобы степени всех его вершин были четными. Найдем все степени в графе, степенью вершины называется число ребер инцидентных данной вершине. Deg(x1)=3, Deg(x2)=5, Deg(x3)=4, Deg(x4)=2, Deg(x5)=8, Deg(x6)=2, Deg(x7)=4, Deg(x8)=4 Есть 2 вершины с нечетными степенями x1 и x2, степень 3 и 5 соответственно Значит эйлерова цикла нет, но есть эйлерова цепь, между вершинами x1 и x2. Найдем ее Добавим фиктивное ребро между x1 и x2. 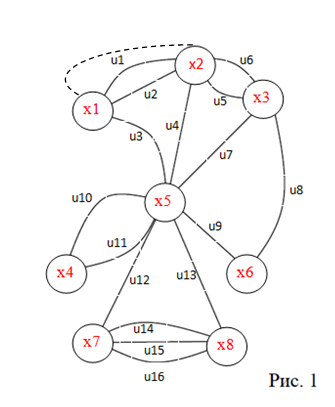 Разобьем новый граф на простые циклы, найдем в нем эйлеров цепь и отбросим потом фиктивное ребро. Получим 6 циклов: x1u1x2u5x3u8x6u9x5u3x1, x2u6x3u7u4x2, x5u10x4u11, x5u12x7u14x8u13x5, x7u15x8u16x7 x1u2x2фиктивное ребро x1 Отбросим фиктивное ребро и получим эйлерова цепь x1u1x2u5x3u8x6u9x5u13x8u14x7u15x8u16x7u12x5u10x4u11x5u7x3u6x2u2x1u3x5 Эйлеровой цепью Ответ : получим эйлерова цепь в неориентированном графе, цепь содержащая все ребра графа x1u1x2u5x3u8x6u9x5u13x8u14x7u15x8u16x7u12x5u10x4u11x5u7x3u6x2u2x1u3x5. Задание 8. Аналитическим способом определить число компонент связности графа. Решение: Построим скелет графа 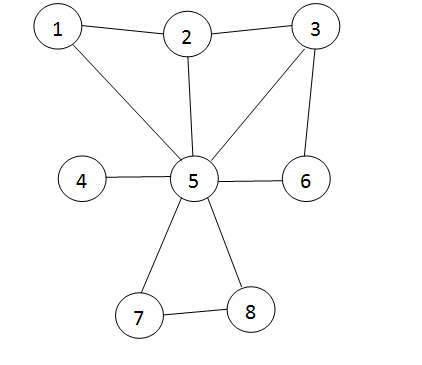 Компонента связности графа– максимальный подграф графа , в котором все вершины попарно достижимы. Найдем количество компонент связности K методом поиска в глубину. Пусть x1 – начальная вершина. Перейдем из нее в вершину x2 по ребру u1, из вершины x2 в вершину x3 по ребру u5, из вершины x3 в вершину x6 по ребру u8, из вершины x6 в вершину x5 по ребру u9, из вершины x5 в вершину x7 по ребру u12, из вершины x7 в вершину x8 по ребру u14 У вершины x8 нет смежных непосещенных вершин, вернемся к вершине x7. У вершины x7 нет смежных непосещенных вершин, вернемся к вершине x5. Перейдем из нее в вершину x4 по ребру u10. У вершины x4 нет смежных непосещенных вершин, вернемся к вершине x5. У вершины x5 нет смежных непосещенных вершин, вернемся к вершине x6. У вершины x6 нет смежных непосещенных вершин, вернемся к вершине x3. У вершины x3 нет смежных непосещенных вершин, вернемся к вершине x2. У вершины x2 нет смежных непосещенных вершин, вернемся к вершине x1. У вершины x1 нет смежных непосещенных вершин. Все вершины графа посещены. Компонента связности найдена К=1. Ответ: у графа изображенного на рисунке 1 компонента связанности равна одному. 1 2 |
