«Дискретная математика лаба 1. лаб раб 1. Лабораторная работа 1 по дисциплине Дискретная математика
 Скачать 1.97 Mb. Скачать 1.97 Mb.
|
|
Министерство науки и высшего образования РФ Федеральное государственное бюджетное образовательное учреждение высшего образования ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ СИСТЕМ УПРАВЛЕНИЯ И РАДИОЭЛЕКТРОНИКИ (ТУСУР) Кафедра компьютерных систем в управлении и проектировании (КСУП) ОТЧЕТ Лабораторная работа № 1 по дисциплине «Дискретная математика»
Санкт-Петербург 2021 Цель лабораторной работы Изучить основные понятия, определения и терминологию теории графов, классы графов, способы задания графа, простейшие операции на графах, числовые характеристики графа и способы их вычисления. 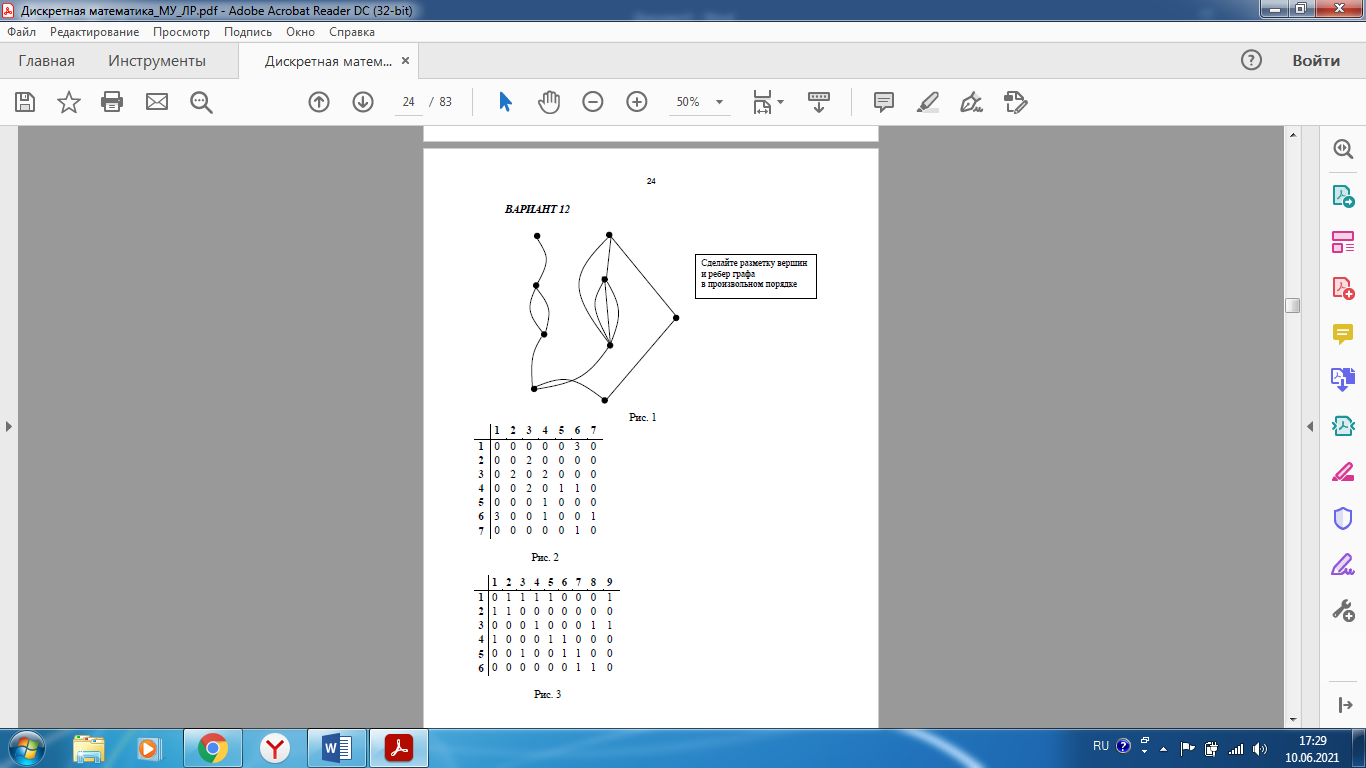 Задание 1. По матрицам (рис. 2 и 3) построить диаграммы графов, определив предварительно вид данных матриц. На рисунке 2 представлена матрица смежности графа. Граф содержит 7 вершин. Т.к. матрица смежности симметрична относительно главной диагонали, граф является неориентированным. На рисунке 3 представлена матрица инцидентности графа. Т.к. все значения в матрице положительные, то граф неориентированный. Граф содержит 6 вершин и 9 ребер. 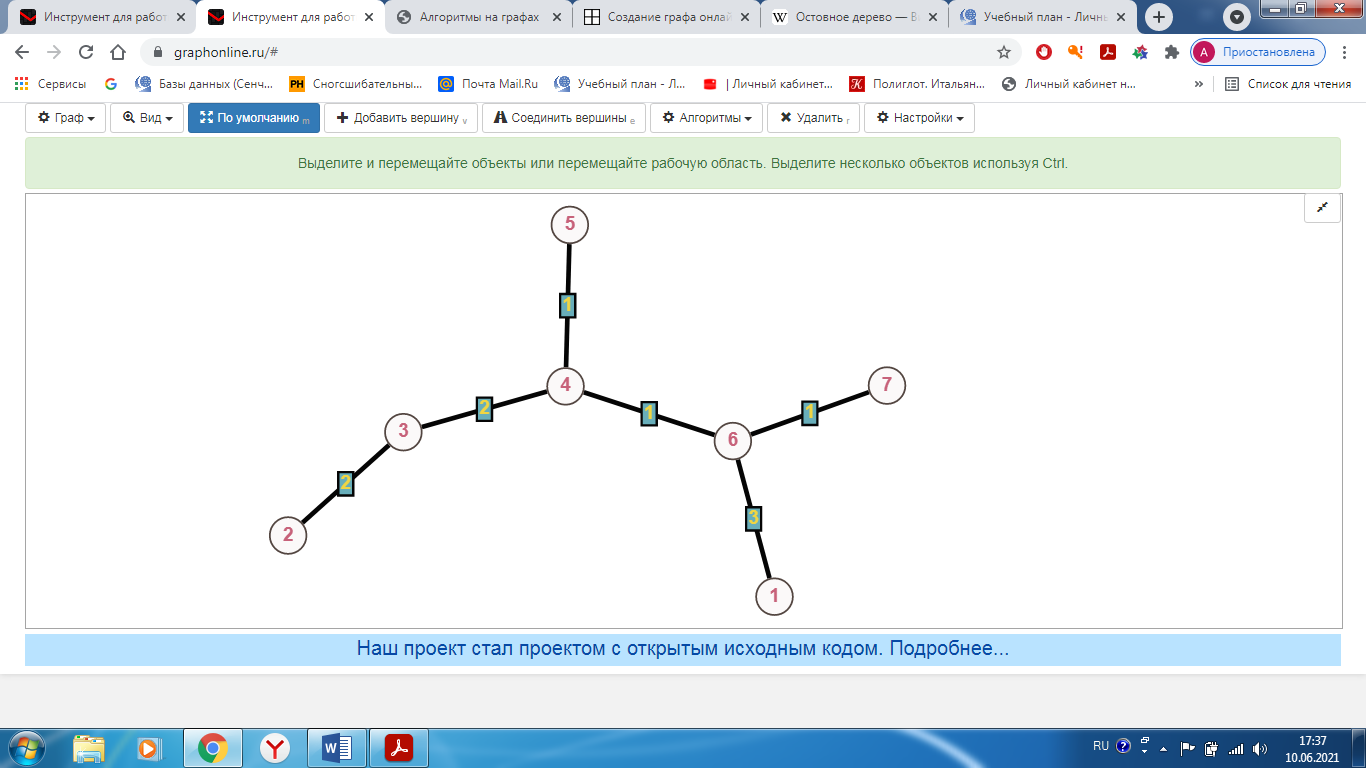  Задание 2. Методами поиска «в глубину» и «в ширину» найти наибольший минимальный маршрут между вершинами графа (рис. 1). 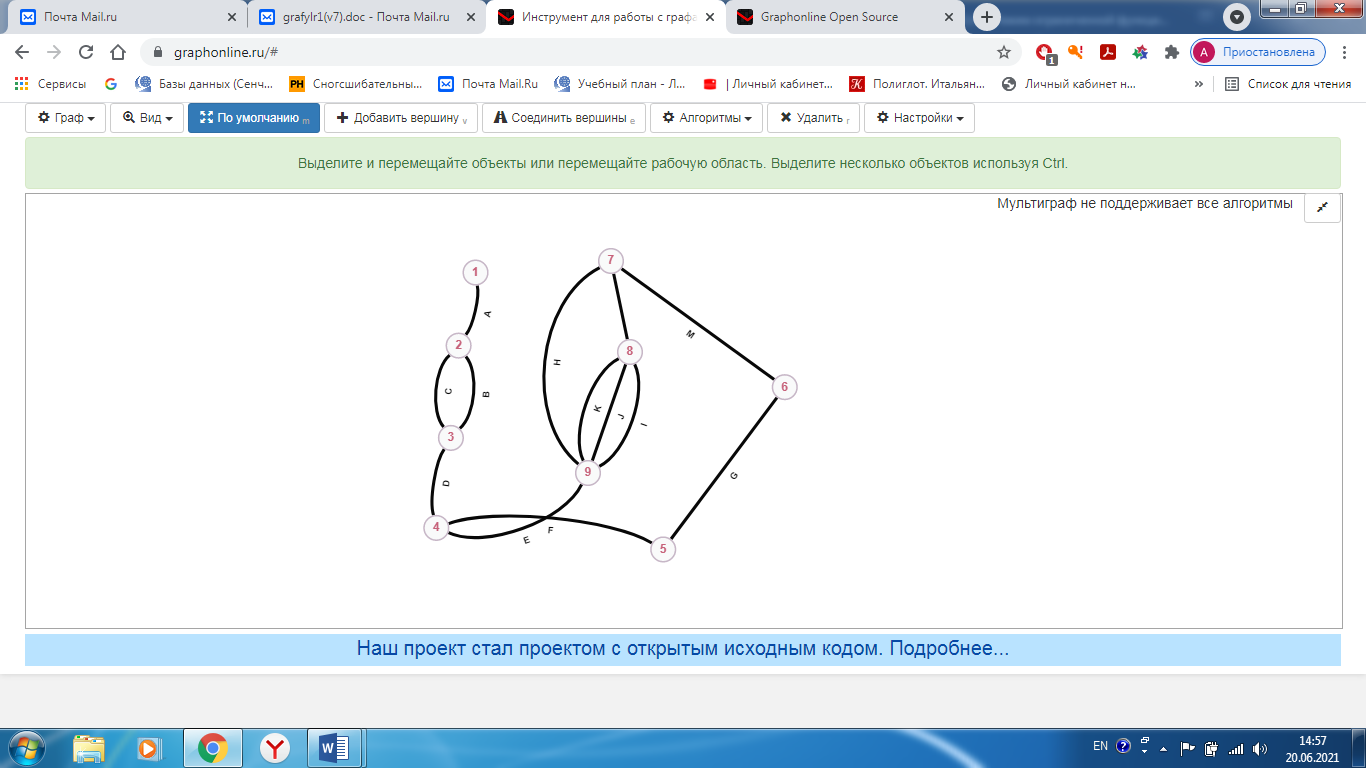 Поиск в «глубину» Начинаем с вершины 1. Из вершины 1 можем перейти в вершину 2 по ребру A Из вершины 2 можем перейти в вершину 3 по ребру B Из вершины 3 можем перейти в вершину 4 по ребру D Из вершины 4 можем перейти в вершину 5 по ребру F Из вершины 5 можем перейти в вершину 6 по ребру G Из вершины 6 можем перейти в вершину 7 по ребру M Из вершины 7 можем перейти в вершину 8 по ребру L Из вершины 8 можем перейти в вершину 9 по ребру I У вершины 9 нет смежных не посещённых вершин. Алгоритм закончен. Получили дерево путей (выделено жёлтым цветом)  Максимальный путь: 1→2→3→4→5→6→7→8→9 Поиск в «ширину» Поиск в ширину — это один из основных алгоритмов на графах. В результате поиска в ширину находится путь кратчайшей длины в невзвешенном графе, т.е. путь, содержащий наименьшее число рёбер. Начинаем с вершины 1. Из вершины 1 можем попасть в вершину 2, добавим ее в очередь: (2). Из вершины 2 можем попасть в вершину 3, добавим ее в очередь и удалим 2: (3) Из вершины 3 можем попасть в вершины 4, добавим ее в очередь и удалим 3: (4) Из вершины 4 можем попасть в вершины 5, 9, добавим их в очередь и удалим 4: (5,9) Из вершины 9 можем попасть в вершины 7,8, добавим их в очередь и удалим 9: (7,8) Из вершины 5 можем попасть в вершину 6, добавим ее в очередь и удалим 5: (6) У вершины 6 нет не посещенных смежных вершин, удаляем ее из очереди () У вершины 7 нет не посещённых смежных вершин, удаляем ее из очереди: () У вершины 8 нет не посещённых смежных вершин, удаляем ее из очереди: () Очередь пуста. Алгоритм закончен. Дерево путей (выделено желтым цветом)  Максимальные пути: 1→2→3→4→5→6 1→2→3→4→9→8 1→2→3→4→9→7 Задание 3. Для каждой пары вершин графа (рис. 1) аналитическим способом вычислить количество маршрутов длины, равной 4, и выделить те пары вершин, для которых их количество ≥ 3, но не более 10. Выписать эти маршруты для какой-либо из выделенных пар. В описании маршрутов указывать вершины и ребра, входящие в него.  Запишем матрицу смежности графа  . Элемент . Элемент 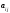 матрицы А равен числу ребер, соединяющих вершины Vi и Vj графа матрицы А равен числу ребер, соединяющих вершины Vi и Vj графа  . .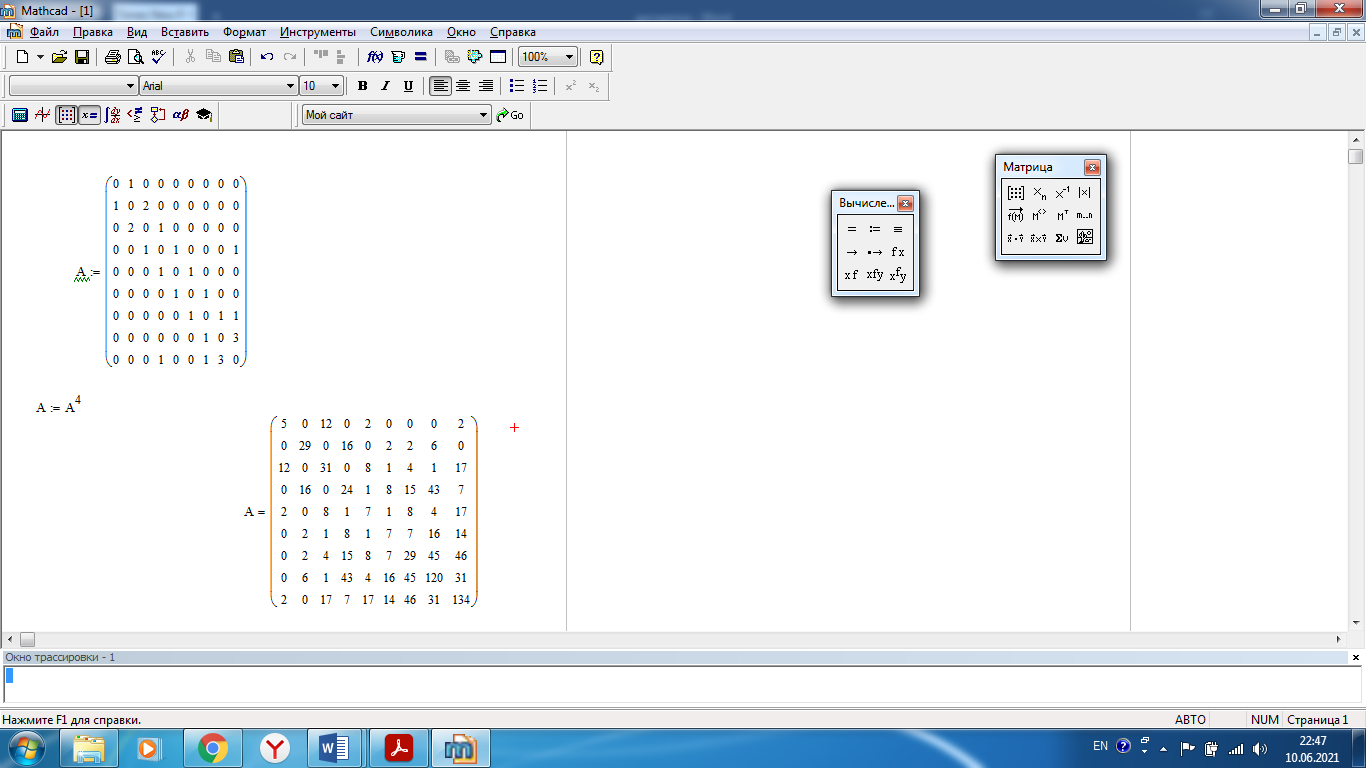 Возведем матрицу смежности в 4ю степень, получим матрицу, в которой каждый элемент aij равен количеству маршрутов длины 4 между вершинами i и j.  В графе 19 пар вершин, для которых количество маршрутов длины 4 не менее 3, но не более 10. Искомые пары вершин: (1,1), (2,8), (3,5), (3,7), (4,7), (4,9), (5,3), (5,5), (5,7), (5,8), (6,4), (6,6), (6,7), (7,3), (7,5), (7,7), (8,2), (8,5), (9,4). Маршруты между вершинами (2,8): 2B3D4F9I 2B3D4F9J 2B3D4F9K 2C3D4F9I 2C3D4F9J 2C3D4F9K Задание 4. Построить матрицу метрики графа. Для этого, для матрицы связности 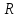 найдём найдём  , затем каждый шаг будем получать , затем каждый шаг будем получать 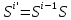 , для всех ячеек, которые являются нулевыми в , для всех ячеек, которые являются нулевыми в  и ненулевыми в и ненулевыми в 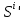 зададим значение зададим значение 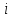 , прочие скопируем из , прочие скопируем из  в в 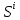 . Если . Если 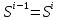 , то завершаем алгоритм, находя матрицу метрики , то завершаем алгоритм, находя матрицу метрики 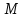 , копируя туда все ненулевые ячейки из , копируя туда все ненулевые ячейки из 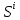 , а вместо нулевых задавая , а вместо нулевых задавая 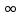 , , 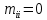 . .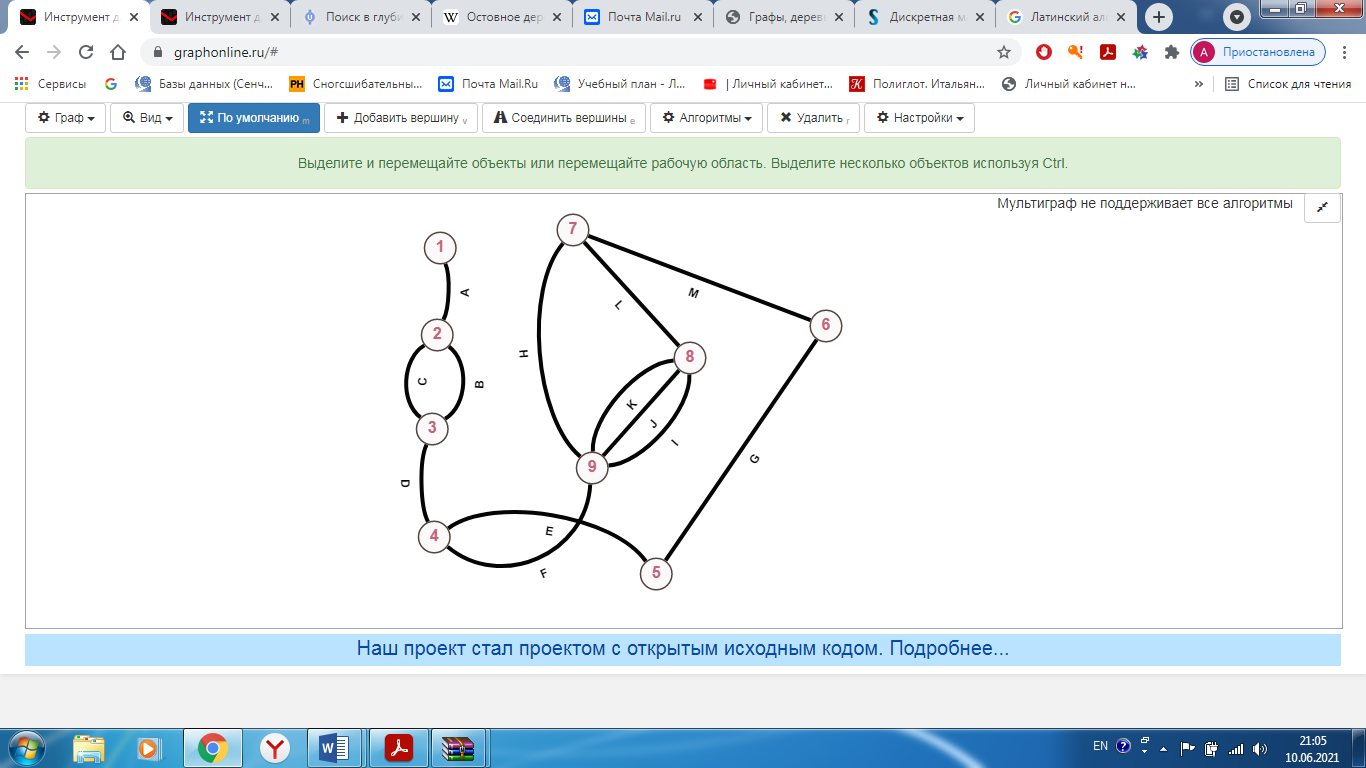  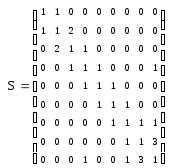     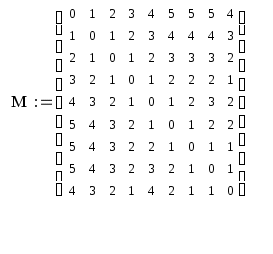 Задание 5. С помощью алгоритма Магу—Вейсмана выполнить правильную раскраску вершин графа с минимальным количеством цветов. По методу Магу - Вейсмана для поиска семейства МВУП составим произведение ПG:  Составим произведение 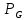 и найдем семейство МВУП: и найдем семейство МВУП:  Для каждого слагаемого преобразованного выражения X1X4X6X8, X1X3X5X9, X1X3X5X8, X1X3X5X7, X1X3X6X9, X1X3X6X8, X1X4X7, X2X4X6X8, X2X5X9, X2X5X8, X2X5X7, X2X6X9. Определяем хроматическое число γ(G) графа G. Упорядочим полученные множества вершин в порядке убывания их кардинальных чисел: X1X3X5X7, X1X3X5X8, X1X3X5X9, X1X3X6X8, X1X3X6X9, X1X4X6X8, X2X4X6X8, X1X4X7, X2X5X7, X2X5X8, X2X5X9, X2X6X9. Припишем вершинам множества X1X3X5X7 цвет «1». Удалим раскрашенные вершины из всех множеств и оставшиеся множества упорядочим в порядке убывания их мощности: X2X4X6X8, X4X6X8, X2X6X9, X6X9, X6X8, X2X9, X2X8, X9, X8, X4, X2. Припишем вершинам множества X2X4X6X9 цвет «2». Удалим раскрашенные вершины из всех множеств и оставшиеся множества упорядочим в порядке убывания их мощности: X9, X9, X9, X9 и припишем ему цвет «3». Всё. Хроматическое число графа:  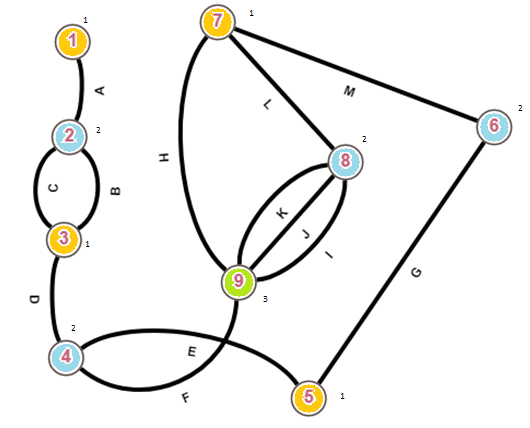 Задание 6. Определить число вершинного покрытия графа (рис. 1).  Вершинное покрытие – это такое множество S вершин графа, что у каждого ребра графа хотя бы один конец входит в S. Алгоритм: На каждом шаге алгоритма производим следующие действия: Выбираем случайное ребро графа e=(u, v). Добавляем в решение S обе выбранные вершины u и v. Удаляем из графа все ребра, инцидентные вершинам u или v. Выберем ребро Е=(4;5) S={4;5} удаляем ребра, инцидентные этим вершинам. 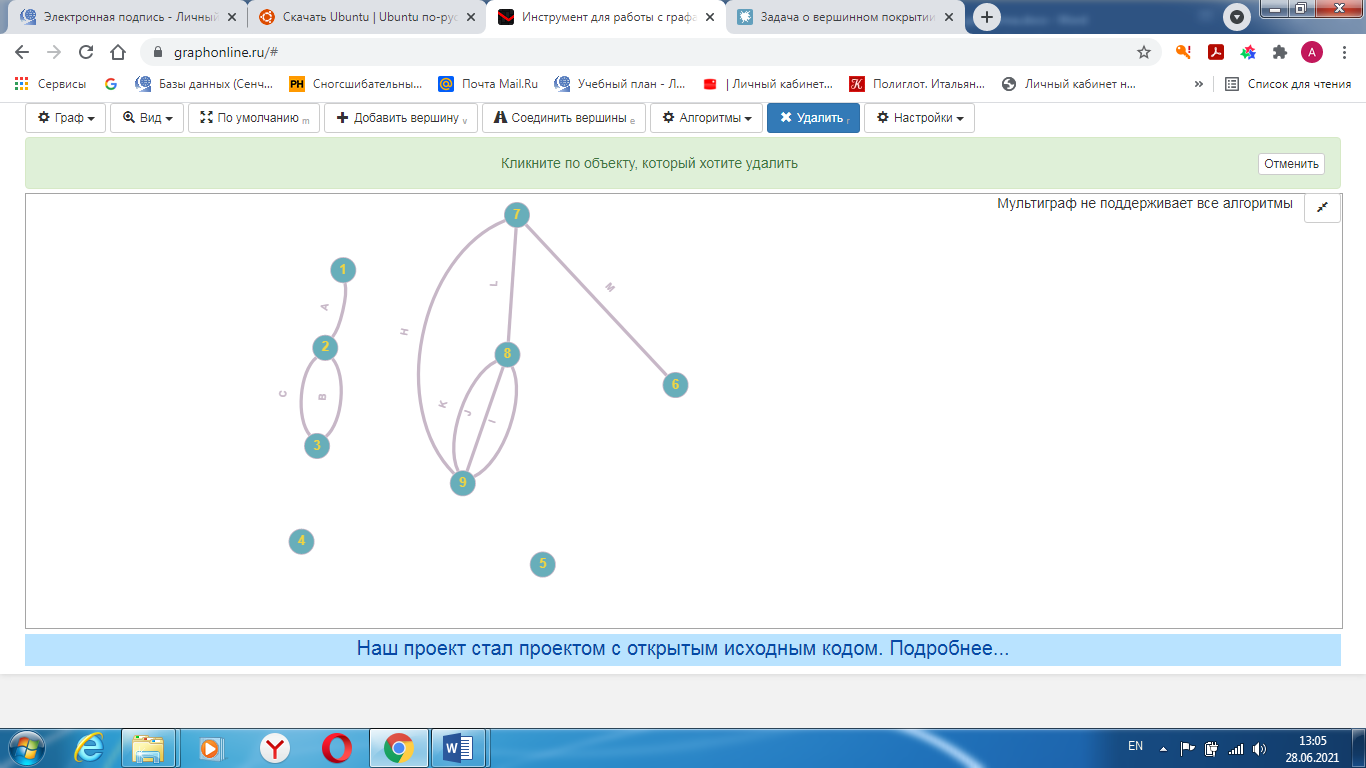 Выберем ребро L=(7;8). Добавляем вершины в S={4,5,7,8}и удаляем инцидентные ребра. 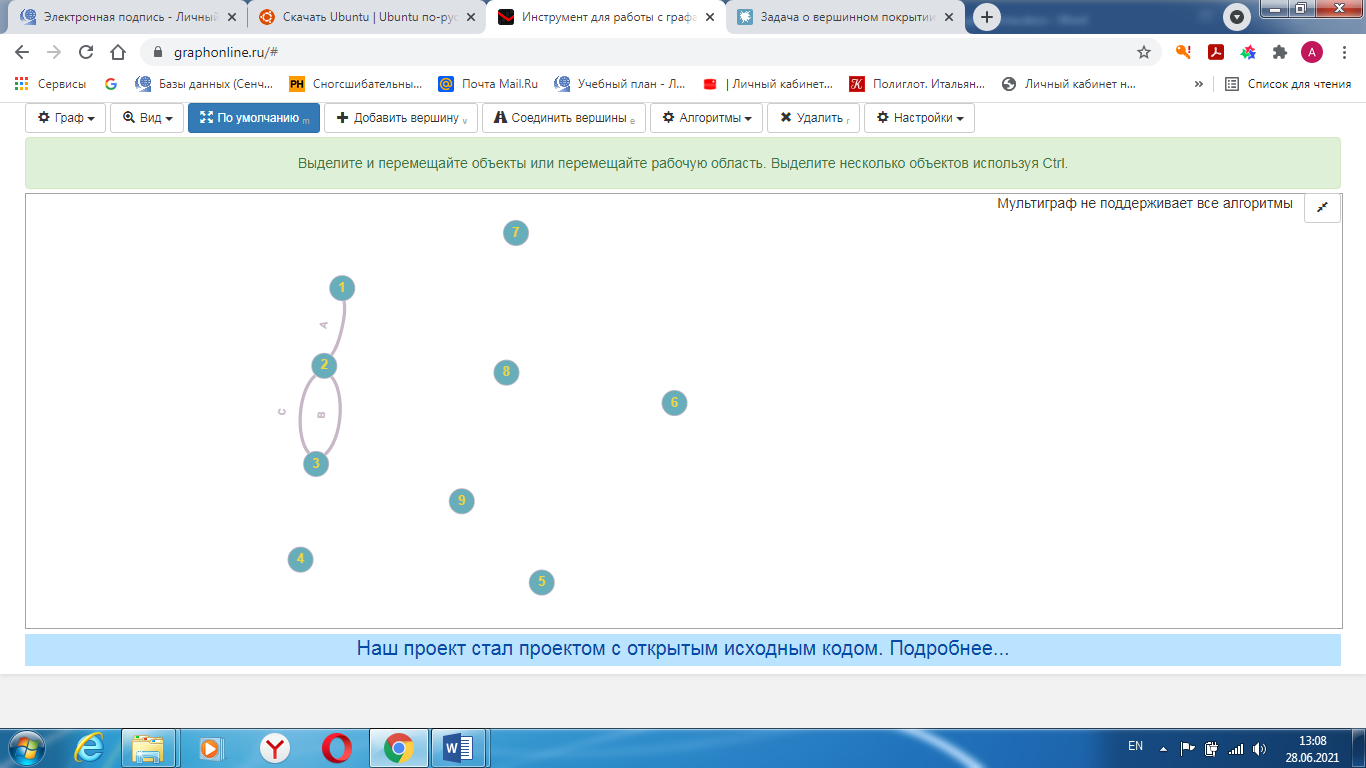 Выберем ребро А=(1;2). Добавляем вершины в S={4,5,7,8,1,2} и удаляем инцидентные ребра.  Число вершинного покрытия S={4,5,7,8,1,2}. Равно 5. Задание 7. Определить содержит ли граф (рис. 1) эйлерову цепь или эйлеров цикл?  Найдем степени вершин графа.
Согласно теореме, доказанной Эйлером, в графе без одиночных вершин эйлеров цикл существует тогда и только тогда, когда граф связный и в нём отсутствуют вершины нечётной степени. Значит, эйлерового цикла в заданном графе нет. Эйлерова цепь в графе существует тогда и только тогда, когда граф связный и содержит не более двух вершин нечётной степени. Значит, в заданном графе нет эйлеровой цепи. Задание 8. Аналитическим способом определить число компонент связности графа. ВАРИАНТ 12 r1,2 = 2 r3,5 = 2 r8,9 = 2 r1,6 = 1 r3,7 = 3 r9,10 = 2 r2,4 = 2 r8,8 = 1 r10,8 = 2 r2,6 = 1 r7,5 = 2 Компонента связности графа — некоторое множество вершин графа такое, что для любых двух вершин из этого множества существует путь из одной в другую, и не существует пути из вершины этого множества в вершину не из этого множества. Построим граф 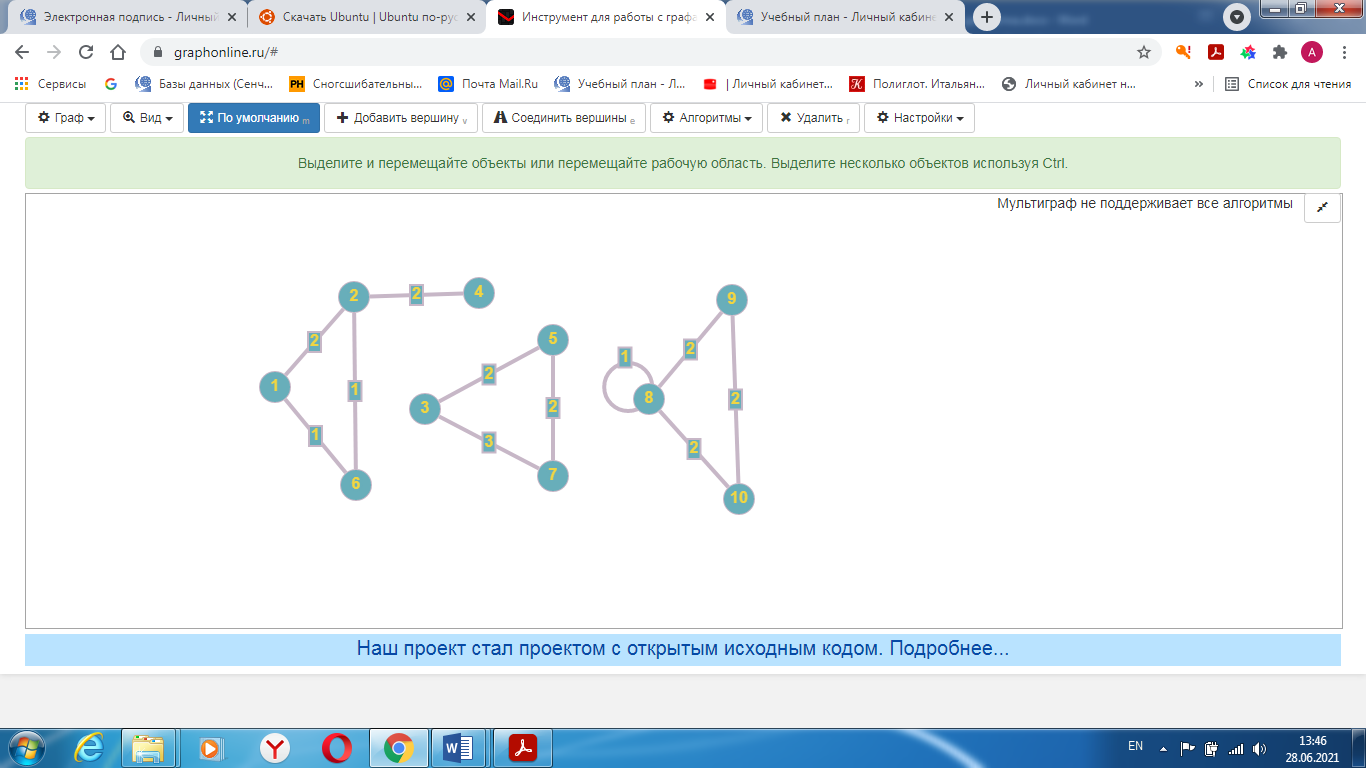 Найдем количество компонент связности K методом поиска в глубину. К=1 Из вершины 1 можем попасть в 2 и 6. У вершины 6 нет смежных не посещённых вершин, вернемся к 2. Из 2 – в 4. У вершины 4 нет смежных не посещённых вершин, вернемся к 2. У вершины 2 нет смежных не посещённых вершин, вернемся к 1. У вершины 1 нет не посещенных вершин. Компонента связности найдена. К=2 Из вершины 3 можем попасть в 5 и 7. У вершины 5 нет смежных не посещённых вершин, вернемся к 7. У вершины 7 нет смежных не посещённых вершин. Компонента связности найдена. К=3 Из вершины 8 можем попасть в 9 и 10. У вершины 9 нет смежных не посещённых вершин, вернемся к 10. У вершины 10 нет смежных не посещённых вершин. Вернемся к 8, у вершины 8 нет не посещенных вершин. Компонента связности найдена. Все вершины графа были посещены. Ответ: К=3. Список литературы: Дискретная математика: учебное пособие / Е.Ф.Жигалова. — Томск: Эль Контент, 2014. — 98 с. 2. Макоха А.Н. Дискретная математика: учеб. пособие для вузов / А.Н.Макоха. —М.: Физматлит, 2005. — 368 с. | ||||||||||||||||||||||||
