Главная страница
Навигация по странице:

  • Найти решение

  • A9:A12

    		•

    лабораторная. Лабораторная работа 1 По дисциплине Основы математического моделирования Вариант 8 Выполнил студент группы грз2011


    Скачать 0.55 Mb.
    НазваниеЛабораторная работа 1 По дисциплине Основы математического моделирования Вариант 8 Выполнил студент группы грз2011
    Дата11.03.2023
    Размер0.55 Mb.
    Формат файлаdocx
    Имя файлалабораторная.docx
    ТипЛабораторная работа
    #980023



    Лабораторная работа №1

    По дисциплине «Основы математического моделирования»

    Вариант 8

    Выполнил студент группы ГРЗ-20-11

    Проверил профессор

    г.Октябрьский

    2022

    Задача. Завод выпускает продукцию в четырех цехах: А, В,С,D,расположенных на разных территориях. Свою продукцию завод поставляет в шесть магазинов города. Цех А производит 130 тыс. шт. изделий, цех В — 90; цех С — 100 и цех D соответственно 140 тыс. шт. изделий. Плановая потребность магазинов в продукции завода следующая: магазин 1 — 110 тыс.шт изделий; магазин 2 — 50 тыс. шт.; магазин 3 — 30 тыс. шт., магазин 4 — 80 тыс. шт., магазин 5 — 100 тыс. шт. и магазин 6 — 90 тыс. шт. изделий. Стоимость перевозки 1 тыс. шт. изделий из цехов в магазины приведена в таблице.

    Цех завода
    Магазины



    М1
    М2
    М3
    М4
    M5
    М6



    А
    2
    3
    6
    8
    2
    10



    В
    8
    1
    2
    3
    9
    5

    С
    7
    6
    4
    1
    5
    9

    D
    2
    10
    8
    5
    3
    4


    Составьте такой план перевозки изделий, при котором расходы на перевозку изделий были бы наименьшими.

    Полностью, условие транспортной задачи, можно представить таблицей следующего содержания:

    Цех завода
    Магазины



    110
    50
    30
    80
    100
    90006
    Bj

    130
    2
    3
    6
    8
    2
    10



    90
    8
    1
    2
    3
    9
    5

    100
    7
    6
    4
    1
    5
    9

    140
    2
    10
    8
    5
    3
    4

    Ai

    Решение:

    1. Выполним проверку сбалансированности математической модели задачи. Модель является сбалансированной, так как суммарный объем производимой продукции в день равен суммарному объему потребности в ней:

    130+90+100+140=460

    110+50+30+80+100+90=460

    1. Откроем новый рабочий лист Excel.

    2. В интервал ячеек A3:A6 вносим запасы поставщиков — Ai: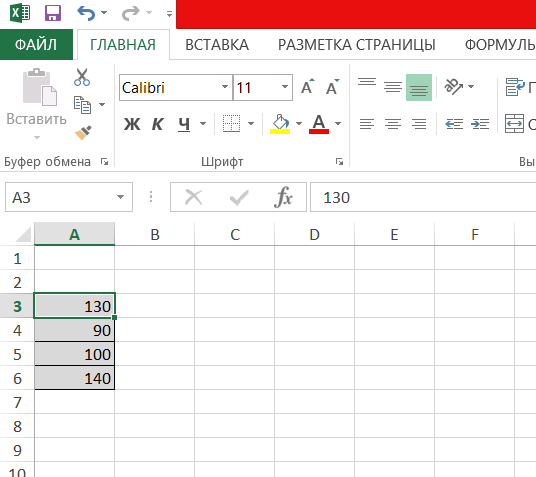




    1. В интервал ячеек B2:G2 вводим количество необходимого груза  Bj–го потребителя: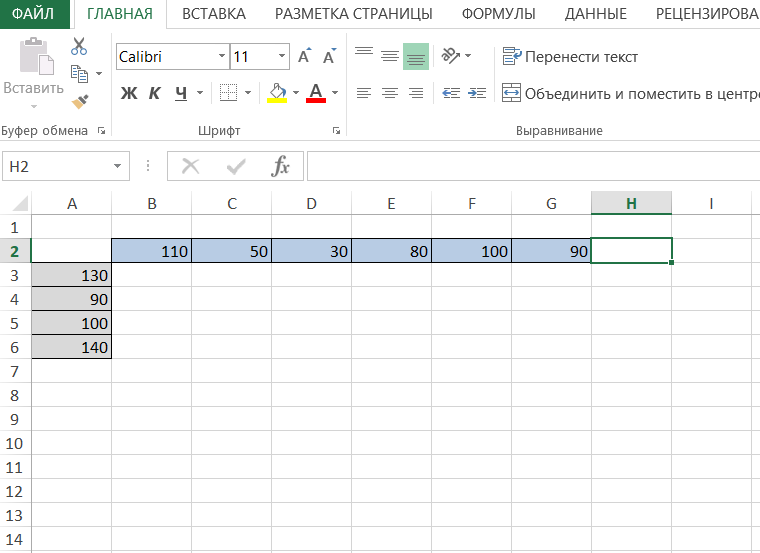




    1. В интервал ячеек B3:G6 вводим матрицу Cij издержек перевозки единицы груза от i-ого поставщика к j-ому потребителю: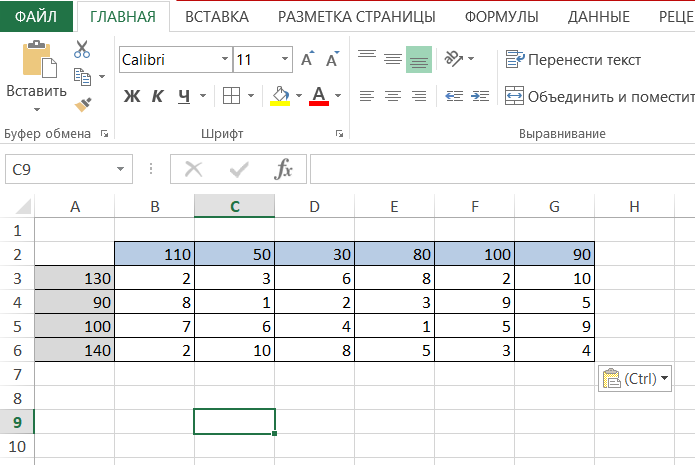




    1. Вячейку Н2 введите формулу: СУММAПРОИЗВ(В3:G6;B9:G12)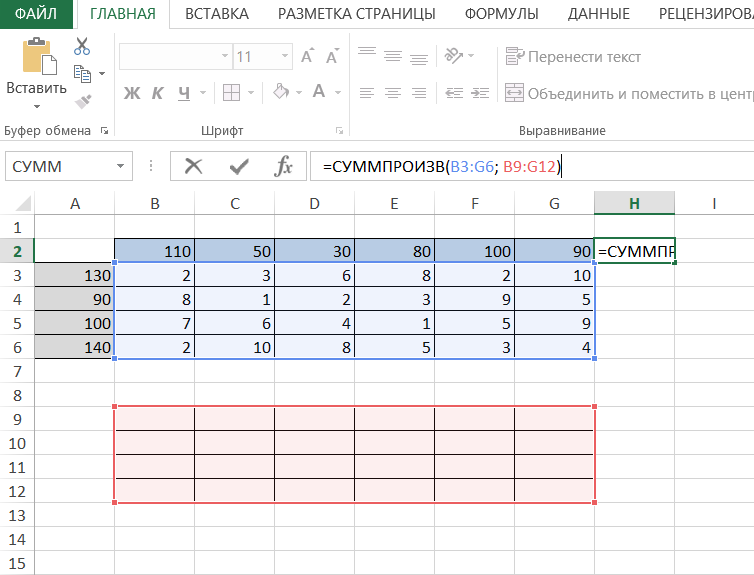 




    1. В ячейку A9 вводим формулу СУММ(B9:G9) и протягиваем её до А12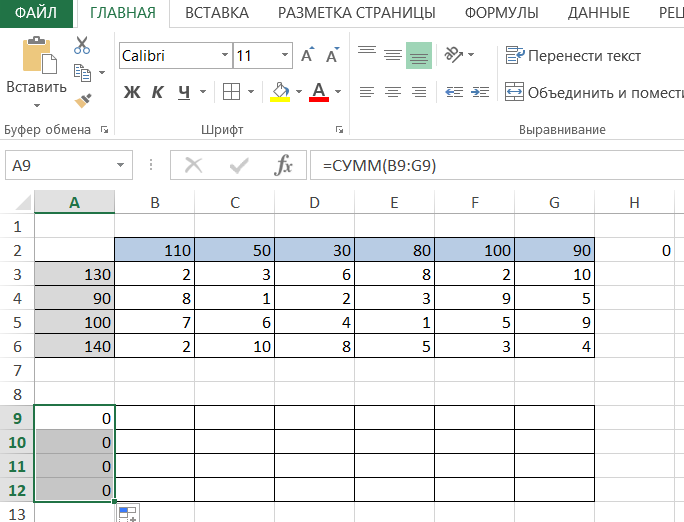



    1. В ячейку B8  вводим формулу СУММ(B9:B12) и протягиваем ее в диапазон от B8 до G8: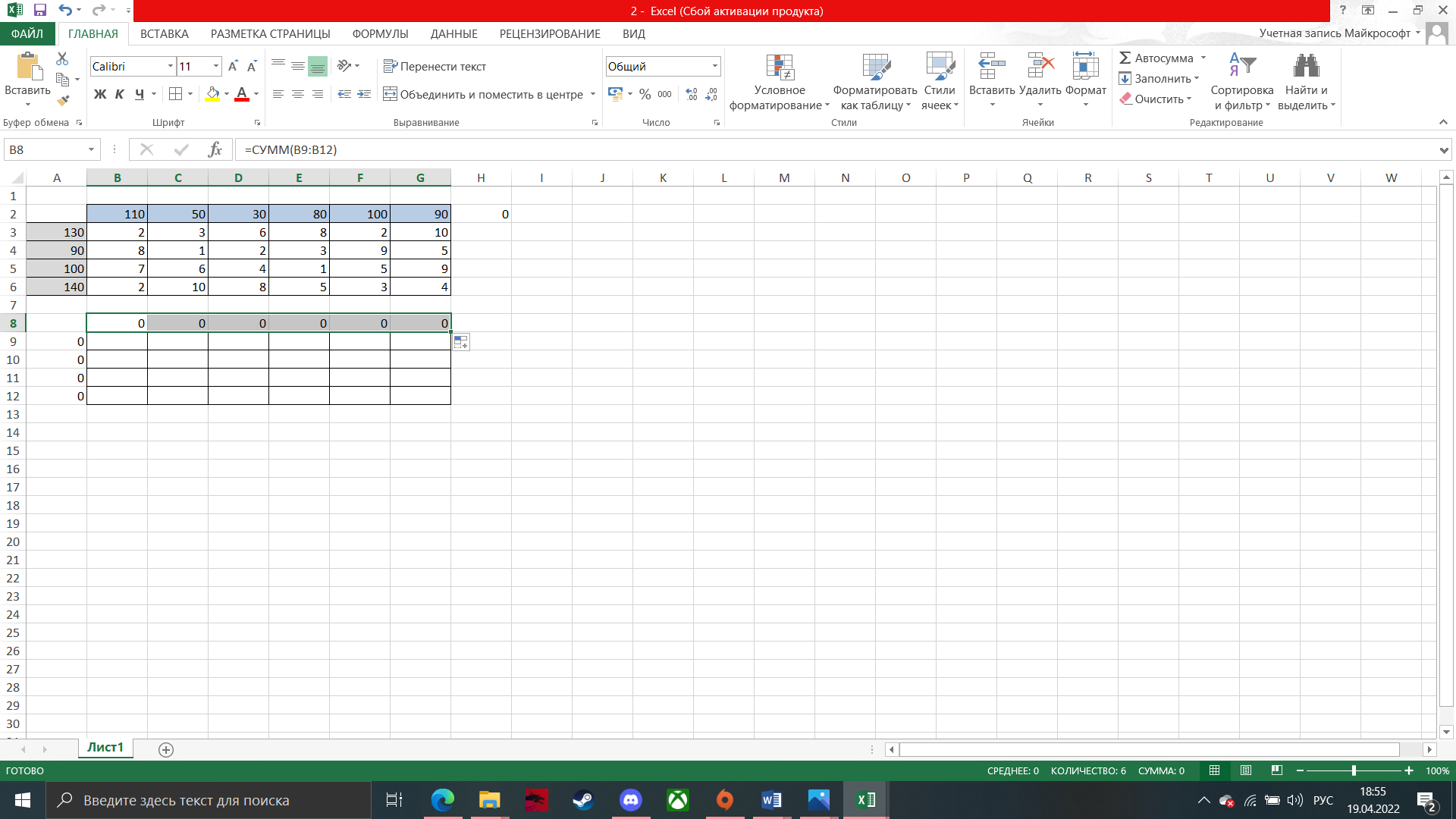




    1. Для решения задачи на панели вкладок выбираем вкладку «Данные», а затем «Поиск решения»:



    1. Заполняем открывшееся окно в соответствие с рисунком и нажимаем

     Найти решение: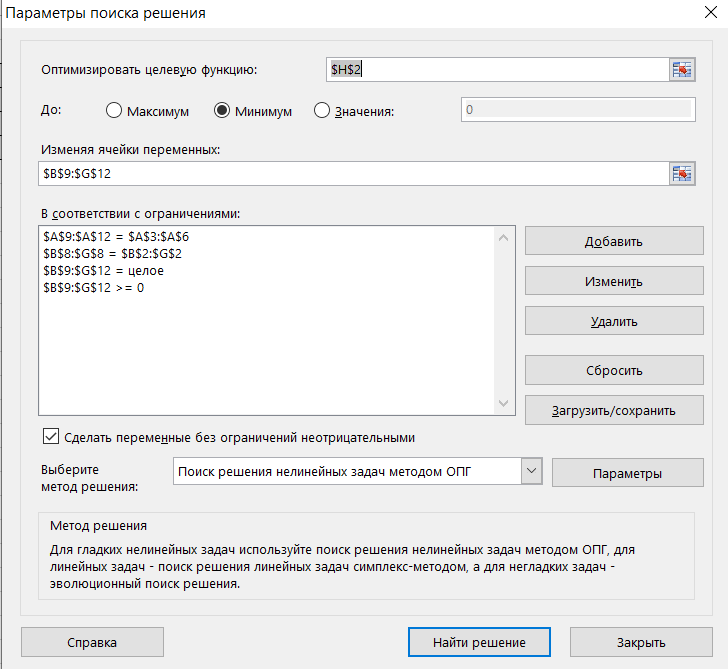

    потребителю на количество единиц груза, которые необходимо перевезти между ними.

     

    1. Оформим  полученный результат и получим следующее: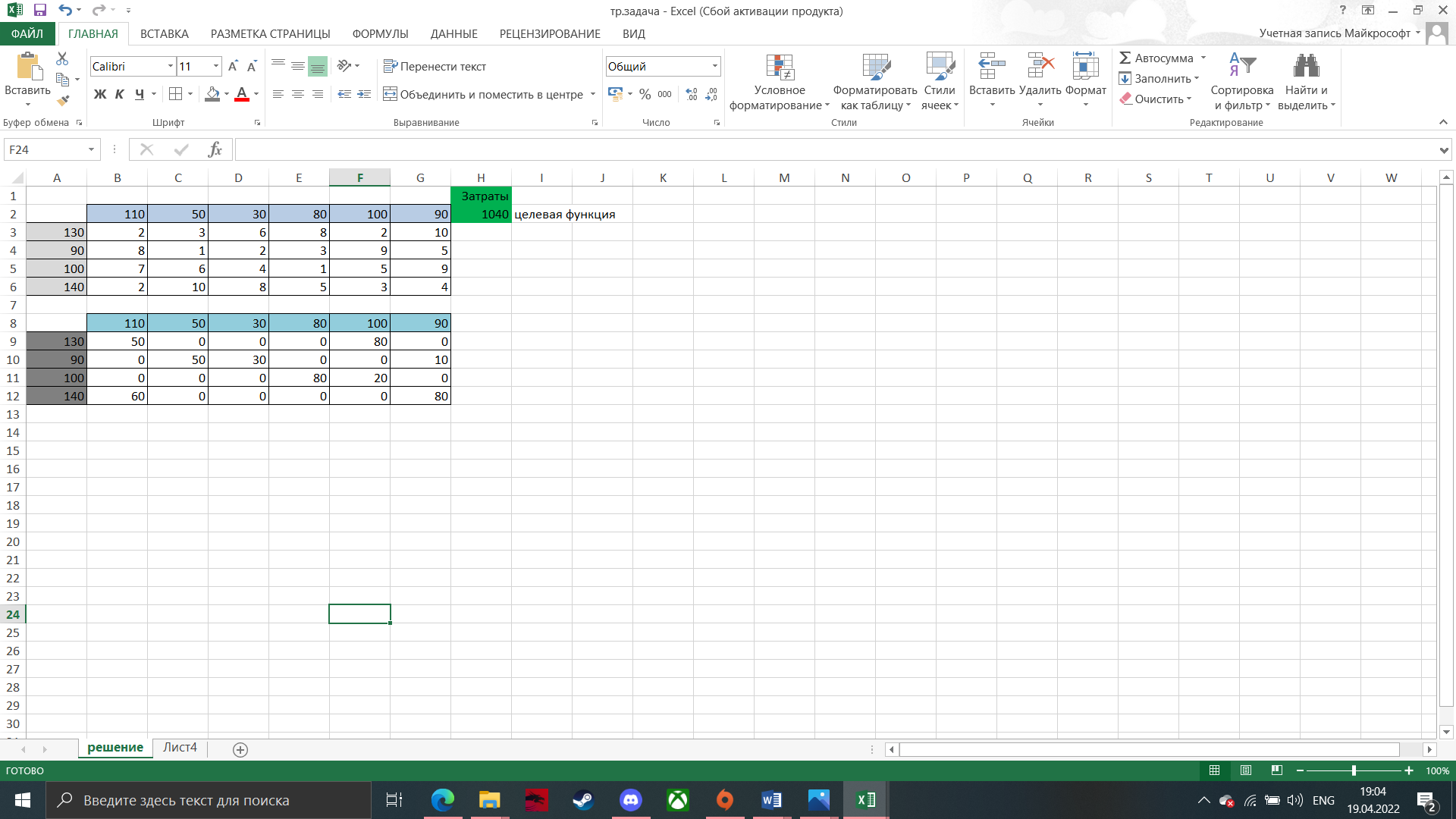




    Вывод:

    В диапазоне B9:G12 получаем результат решения транспортной задачи (т.е. значение в ячейке соответствует количеству груза перевезенного от i-ого поставщика к j-ому потребителю).

     

    В диапазоне A9:A12 количество груза, которое необходимо вывезти от поставщиков.

     

    В диапазоне B8:G8 количество которое будет доставлено потребителям согласно найденному решению.

     

    В ячейке H2 значение целевой функции при найденном решении (минимально возможное). Это значение получено в результате умножения стоимости перевозки от от i-ого поставщика к j-ому потребителю на количество единиц груза, которые необходимо перевезти между ними.

    написать администратору сайта