ОТЧЁТ по Лабораторной работе №2 “Удаление невидимых линий у многогранников”. Лабораторная работа 1 по дисциплине Вычислительная математика Вариант 5 Выполнили Проверил
 Скачать 0.84 Mb. Скачать 0.84 Mb.
|
|
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ ФЕДЕРАЛЬНОЕ государственное БЮДЖЕТНОЕ образовательное учреждение высшего образования «НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ» Кафедра систем сбора и обработки данных  Лабораторная работа №1 по дисциплине: « Вычислительная математика » Вариант № 5 Выполнили Проверил Студенты гр. АО-12 Уберт Алексей Игоревич Васютич С.В. Смыков Е.Д. Новосибирск 2022 Цель работы Ознакомиться с квадратурными формулами Ньютона-Котеса численного интегрирования, исследовать влияние порядка точности квадратурной формулы и шага интегрирования на точность вычисления определенного интеграла. Постановка задачи Вычислить определенный интеграл 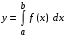 , , 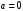 , , 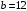 от функции 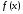 , заданной на , заданной на 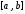 с шагом с шагом 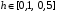 посредством квадратурных формул Ньютона-Котеса порядка точности посредством квадратурных формул Ньютона-Котеса порядка точности 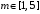 (при (при 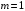 имеет место формула левых прямоугольников). имеет место формула левых прямоугольников).При вычислении погрешностей интегрирования 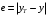 за точное значение интеграла за точное значение интеграла 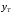 принимается результат интегрирования, полученный с минимальным шагом принимается результат интегрирования, полученный с минимальным шагом 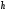 и максимальным порядком и максимальным порядком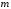 . .Квадратурные формулы (обобщенные) для 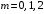 . .При m = 0: 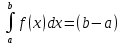 При m = 1: 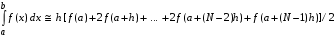 . .При m = 2: 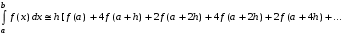 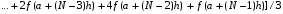 . .Результаты вычислений (значения интегралов). Значения интеграла, высчитанные по изменению порядка точности: 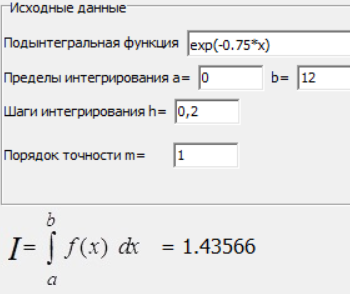 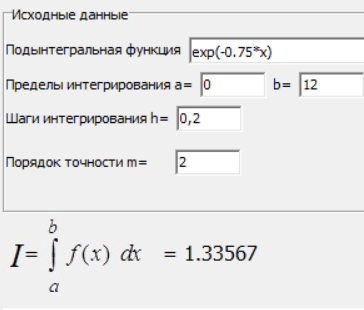 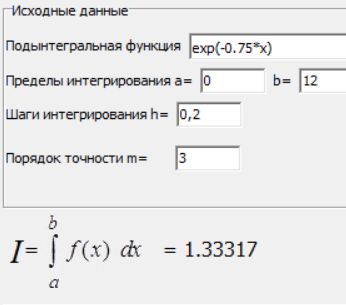 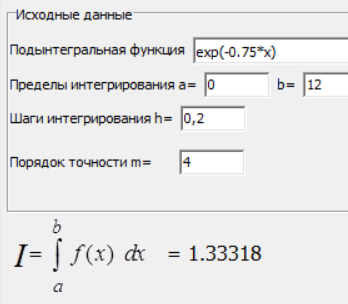 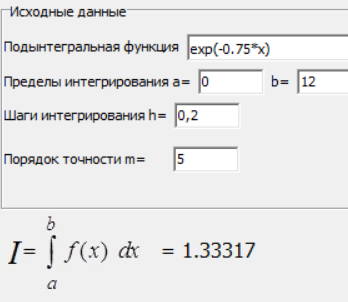 Значения интеграла, высчитанные по изменению шага: 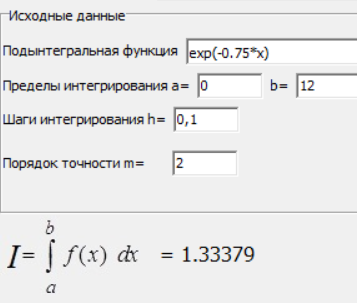 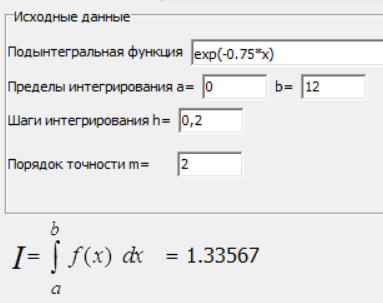 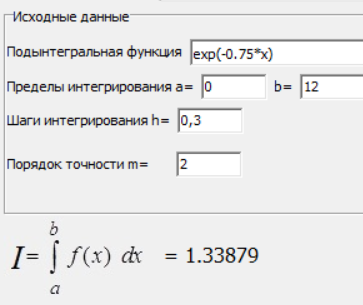 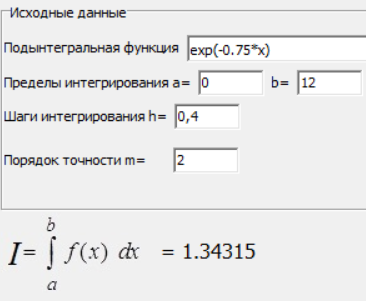 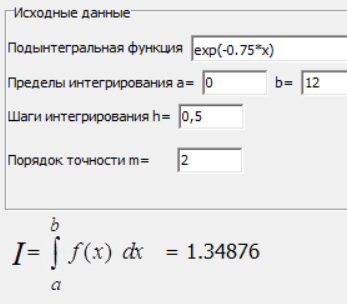 График исследуемой функции и погрешностей, от шага и порядка точности 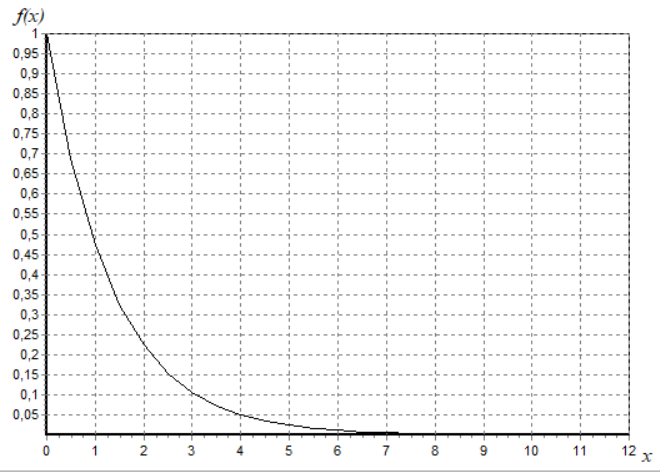 График по порядку точности: 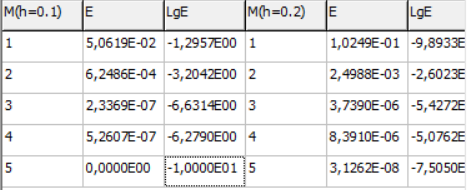 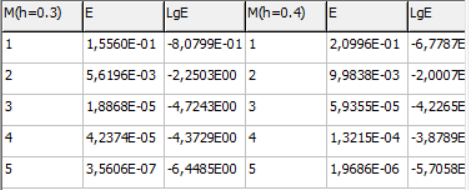 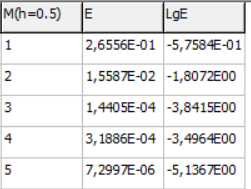 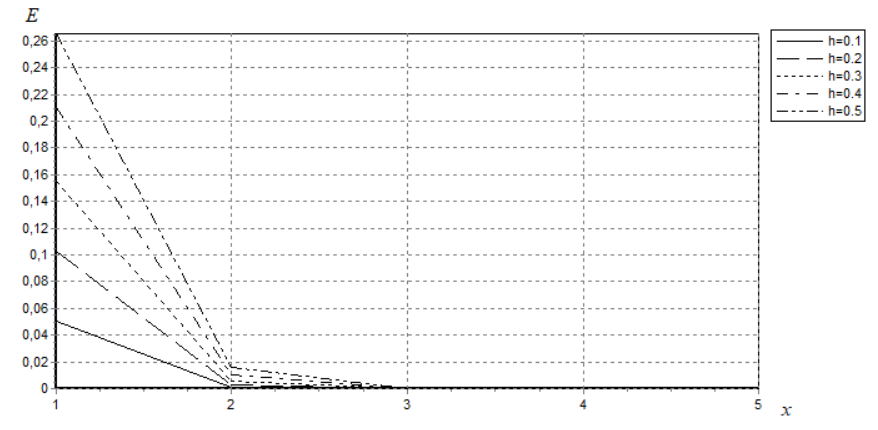 График по шагу: 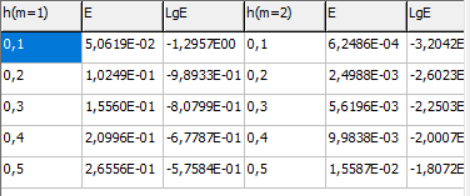 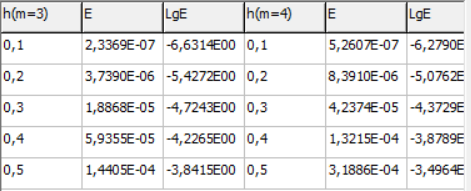 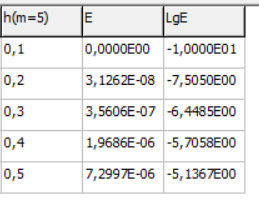 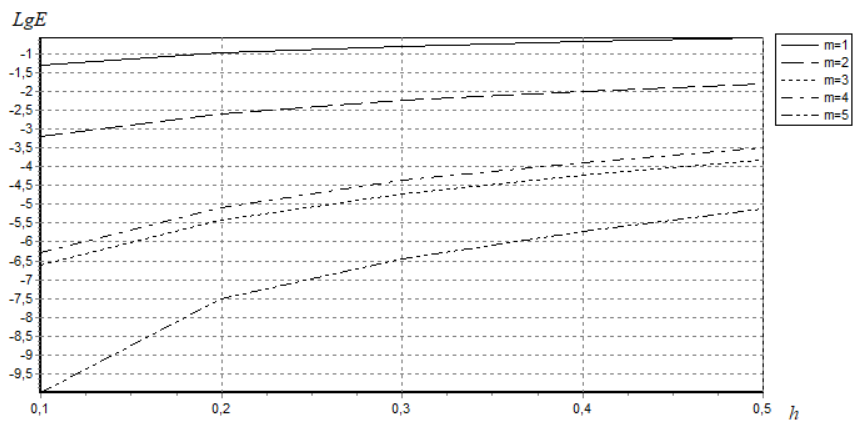 |
