Исследование логических схем на элементах «И–НЕ». лр1. Лабораторная работа 1 По дисциплине Вычислительная техника и информационные технологии
 Скачать 1.03 Mb.
|
|
Федеральное агентство связи Сибирский Государственный Университет Телекоммуникаций и Информатики Межрегиональный центр переподготовки специалистов Лабораторная работа №1По дисциплине: Вычислительная техника и информационные технологииВыполнил: Группа: Вариант: 21 Проверил: ___________________ Новосибирск, 2014 г Лабораторная работа №1 Исследование логических схем на элементах «И–НЕ» 1. Цель работы Изучение свойств логических элементов «И–НЕ»; приобретение навыков синтеза логических схем. 2.Подготовка к работе 2.1. Изучить основные логические функции и их условное обозначение, способы представления логических функций, основные правила выполнения логических операций, функционально полные системы логических элементов. 2.2. Синтезировать логические выражения, реализующие в базисе И – НЕ следующие логические функции: НЕ, ИЛИ, И, ИЛИ – НЕ, И – НЕ, И – ИЛИ – НЕ, неравнозначность (исключающее ИЛИ), равнозначность (исключающее ИЛИ – НЕ). По полученным выражениям составить схемы логических функций и записать для них таблицы истинности. 3. Описание схемы 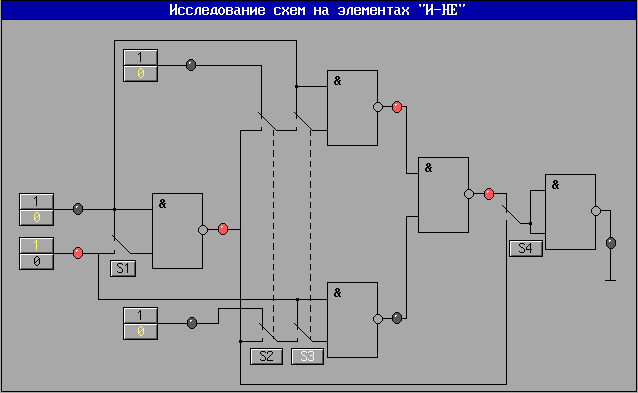 Рис.1 Функциональная схема (рис.1) лабораторной работы представляет собой упорядоченное соединение 5 двухвходовых логических элементов, выполняющих логические операции И – НЕ. Коммутация цепей производится с помощью переключателей S 1 – S 4 путем щелчка указателя мыши на изображении ключа. Обратите внимание на то, что переключатели S 2 и S 3 – сдвоенные. Входные сигналы логических уровней «0» и «1» выбираются нажатием на соответствующие кнопки источников. Красное свечение лампочки свидетельствует о том, что в данном узле схемы действует логическая «1», отсутствие свечения лампочки соответствует сигналу логического «0». 4. Задание к лабораторной работе Экспериментально исследовать правила построения различных логических функций в базисе И-НЕ, снять таблицы истинности для указанных выше логических функций. Логическая функция «НЕ» 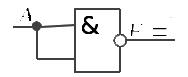  Рис.2 Функциональная схема Таблица 1 Таблица истинности
Логическая функция «ИЛИ»  В базисе И-НЕ: 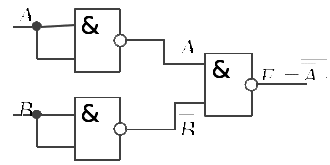  Рис.3 Функциональная схема Таблица 2 Таблица истинности
Логическая функция «И»  В базисе И-НЕ: 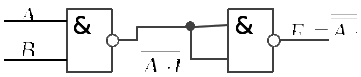  Рис.3 Функциональная схема Таблица 3 Таблица истинности
Логическая функция «ИЛИ-НЕ»  В базисе И-НЕ: 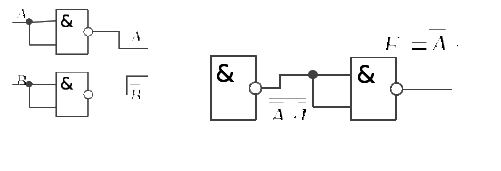  Рис.4 Функциональная схема Таблица 4 Таблица истинности
Логическая функция «И-НЕ» 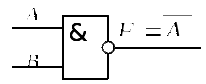  Рис.5 Функциональная схема Таблица 5 Таблица истинности
Логическая функция «И-ИЛИ-НЕ»  В базисе И-НЕ: 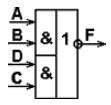  Рис.6 Функциональная схема Таблица 6 Таблица истинности
Логическая функция «неравнозначность (исключающая ИЛИ)»  В базисе И-НЕ: 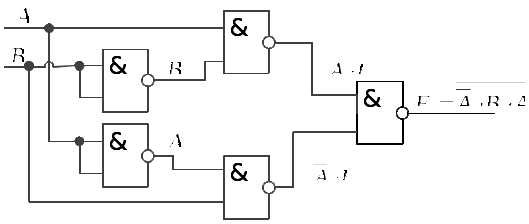  Рис.7 Функциональная схема Таблица 7 Таблица истинности
Логическая функция «равнозначность (исключающая ИЛИ-НЕ)»  В базисе И-НЕ: 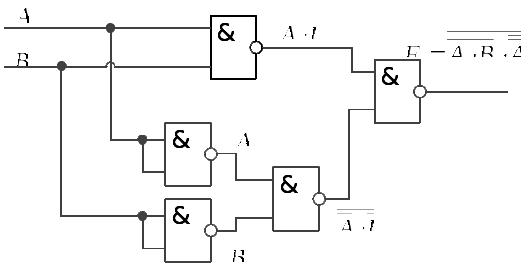  Рис.8 Функциональная схема Таблица 8 Таблица истинности
Таблицы истинности снятые экспериментально - Логическая функция «НЕ» Таблица 9 Таблица истинности
- Логическая функция «ИЛИ» Таблица 10 Таблица истинности
- Логическая функция «И» Таблица 11 Таблица истинности
- Логическая функция «ИЛИ-НЕ» Таблица 12 Таблица истинности
- Логическая функция «И-НЕ» Таблица 13 Таблица истинности
- Логическая функция «И-ИЛИ-НЕ» Таблица 14 Таблица истинности
- Логическая функция «неравнозначность (исключающая ИЛИ)» Таблица 15 Таблица истинности
- Логическая функция «равнозначность (исключающая ИЛИ-НЕ)» Таблица 16 Таблица истинности
Вывод: - Изучены основные логические функции и их условное обозначение, способы представления логических функций, основные правила выполнения логических операций, функционально полные системы логических элементов; - Таблицы истинности полученные экспериментальным путем согласуются с таблицами истинностей полученными при подготовке к работе. Контрольные вопросы: 1. Что такое полный и минимальный базис? Имея элементы, осуществляющие элементарные операции f0,..., f15 можно выполнить любую сложную логическую операцию. Такую систему функций можно назвать полной системой, или полным базисом. Условие наличия 16 различных типов логических элементов, каждый из которых реализует одну из 16 элементарных функций /о,..., /is, является достаточным для синтеза логического устройства любой сложности, но оно не является необходимым, т. е. при синтезе можно ограничиться меньшим набором элементарных функций, взятых f0,..., f15. Последовательно исключая из базиса функции, можно получить так называемый минимальный базис. Под минимальным базисом понимают такой набор функций, исключение, из которого любой функции превращает полную систему функций в неполную. Возможны различные базисы и минимальные базисы, отличающиеся друг от друга числом входящих в них функций и видом этих функций. Выбор того или иного базиса для синтеза логических устройств связан с тем, насколько просто, удобно и экономично технически выполнить элементы, реализующие входящие в базис функции, и в целом все логическое устройство. 2. Почему логический элемент И – НЕ обладает функциональной полнотой? Существуют такие наборы логических функций, с помощью которых можно выразить любые другие логические функции. Они называются функционально полными или базисами. Наиболее известный базис - это набор функций И, ИЛИ, НЕ. Функция штрих Шеффера (И – НЕ) является базисной. Так как с помощью логических элементов И-НЕ можно собрать любую логическую схему. На таких элементах собран микропроцессор компьютера и другие логические устройства. Логические схемы состоят из логических элементов, осуществляющих логические операции. 3. Основные свойства логических функций. Логическая функция - это функция логических переменных, которая может принимать только два значения: 0 или 1. В свою очередь, сама логическая переменная (аргумент логической функции) тоже может принимать только два значения: 0 или 1. Это и является основным свойством логической функции. Логические функции характеризуются таблицами истинности. Определим логические функции:  - логическое умножение (конъюнкция),  - логическое сложение (дизъюнкция),  - логическое умножение с инверсией,  - логическое сложение с инверсией,  — суммирование по модулю 2,  - равнозначность. 4. Дайте формулировку правила де Моргана. Смысл законов де Моргана (Август де Морган (1806-1871) - шотландский математик и логик) можно выразить в кратких словесных формулировках:  - отрицание логического произведения эквивалентно логической сумме отрицаний множителей. - отрицание логической суммы эквивалентно логическому произведению отрицаний слагаемых.5. Какова цель минимизации логических функций? Под минимизацией понимают преобразование логических функций. Цель минимизации логических функций заключается в упрощении их аналитического представления. Существуют два направления минимизации: 1. Кратчайшая форма записи (цель – минимизировать ранг каждого терма). При этом получаются кратчайшие формы КДНФ, ККНФ, КПНФ. 2. Получение минимальной формы записи (цель – получение минимального числа символов для записи всей функции сразу). |