Лабораторная работа 1 Почему анализ называется линейным

• Название: Лабораторная работа 1 Почему анализ называется линейным
• Дата: 20.03.2021
• Размер: 97.11 Kb.
• Имя файла: 9074 (1).docx
• Тип: Лабораторная работа; #186496

Примерные вопросы при онлайн-защите лабораторных работ

Лабораторная работа 1

1. 
   
   Почему анализ называется линейным?
   

Линейная регрессия - выраженная в виде прямой зависимость среднего значения какой-либо величины от некоторой другой величины.

2. 
   
   Почему анализ называется регрессионным?
   

Регрессионный анализ (regression analysis) – это метод изучения статистической взаимосвязи между одной зависимой количественной зависимой переменной от одной или нескольких независимых количественных переменных.

3. 
   
   Почему анализ называется парным?
   

Парный регрессионный анализ – это метод математической статистики, который позволяет найти наиболее точное и достоверное отображение (модель, аппроксимацию) стохастической зависимости между откликом Y и одним из факторов X.

4. 
   
   Какой показатель использовался как факторный, какой- как результативный?
   

Факторный анализ – это анализ влияния отдельных факторов на результативный показатель с помощью детерминированных или стохастических приемов исследования.

5. 
   
   Как выглядит уравнение регрессии в парном линейном регрессионном анализе?
   
6. 
   К
   ак выглядит оцененное уравнение?
   

Y = a+bx+E

i=1,…n

7. 
   
   Почему в модели появляются остатки?
   

Остатки – результат деятельности большого числа различных факторов, поэтому логично ожидать, что ни один из этих факторов не должен оказывать большего влияния, чем остальные. Остатки должны представлять собой случайные величины, а значит подчиняться закону нормального распределения. Это означает следующее: основная масса точек должна лежать близко к регрессионной прямой, а чем дальше от прямой, тем точек должно быть меньше

8. 
   
   Каким методом получаются значения коэффициентов модели? В чем суть этого метода?
   

Метод наименьших квадратов

Общий смысл оценивания по методу наименьших квадратов заключается в минимизации суммы квадратов отклонений наблюдаемых значений зависимой переменной от значений, предсказанных моделью.

9. 
   Сколько получился, что показывает и в чем измеряется коэффициент a? (в контексте рассматриваемой проблемной ситуации);
   

а = 8,0626615

10. 
    Сколько получился, что показывает и в чем измеряется коэффициент b? (в контексте рассматриваемой проблемной ситуации);
    

b = 0,9373385

11. 
    
    Каково направление связи между фактором и результативным показателем (зависимой переменной)?
    

Стохастический (корреляционный) – связь между результативным и факторными показателями является неполной или вероятностной.

12. 
    
    Чем прямая связь отличается от обратной?
    

По направлению корреляционная связь бывает положительной («прямой») и отрицательной («обратной»).

При прямой (обратной) связи увеличение одной из переменных ведет к увеличению (уменьшению) условной (групповой) средней другой.

13. 
    
    Что показывает коэффициент детерминации?
    

Он показывает, какая доля дисперсии результативного признака объясняется влиянием независимых переменных.

14. 
    
    Какой вывод сделали на основе коэффициента детерминации?
    

Коэффициент детерминации показывает, какую часть вариации (дисперсии) зависимой переменной Y воспроизводит (объясняет) построенное уравнение регрессии. В нашем случае построенное уравнение регрессии на 38,7% объясняет зависимость переменной Y от переменной X.

15. 
    
    Как обозначаются расчетные значения результативного показателя?
    

Y = 0,937339+ 8,062661*X.

16. 
    
    Как рассчитываются прогнозные (расчетные) значения результативного показателя?
    

Результативный показатель факторной модели представлен в виде произведения, частного или алгебраической суммы факторов.

17. 
    
    Как обозначается коэффициент детерминации?
    

R^2

18. 
    
    В чем он измеряется и каких пределах может варьировать?
    

Доля дисперсии зависимой переменной, 02<1, R²=1

19. 
    
    Каковы недостатки коэффициента детерминации? Какой коэффициент позволяет их решить?
    

Основная проблема применения (выборочного) заключается в том, что его значение увеличивается (не уменьшается) от добавления в модель новых переменных, даже если эти переменные никакого отношения к объясняемой переменной не имеют! Поэтому сравнение моделей с разным количеством факторов с помощью коэффициента детерминации, вообще говоря, некорректно. Для этих целей можно использовать альтернативные показатели.

скорректированный коэффициент детерминации , в котором используются несмещённые оценки дисперсий.

20. 
    
    В каких пределах находится скорректированный коэффициент детерминации?
    

От 0 до 1

21. 
    
    Что означает термин «значимость»?
    

Значимость F – это вероятность значимости для F критерия

22. 
    Какова нулевая гипотеза в F-критерии (в контексте рассматриваемой проблемной ситуации);
    

Коэффициент корреляции = 1,716439

23. 
    Какова альтернативная гипотеза в F-критерии? (в контексте рассматриваемой проблемной ситуации);
    

= 2,306

24. 
    
    В результате выполнения F-критерия нулевая гипотеза была принята или отвергнута? Почему?
    

В результате выполнения F-критерия альтернативная гипотеза была принята или отвергнута? Почему?

Поскольку |tкрит| > tрасч, то нулевую гипотезу о равенстве нулю коэффициента корреляции отвергаем с вероятностью ошибки меньше 5% и делаем вывод о значимости коэффициента корреляции.

25. 
    Какова нулевая гипотеза в t-критерии для коэффициента b? (в контексте рассматриваемой проблемной ситуации);
    

Какова альтернативная гипотеза в t-критерии для коэффициента b? (в контексте рассматриваемой проблемной ситуации);

В результате выполнения t-критерия для b нулевая гипотеза была принята или отвергнута? Почему?

В результате выполнения t-критерия для b альтернативная гипотеза была принята или отвергнута? Почему?

b = 0,937339

Нулевая гипотеза принята, так как коэффициент b меньше расчетного, то есть альтернативного (2,306).

26. 
    
    Как на основе доверительных интервалов для оценок коэффициентов регрессии можно сделать вывод об их значимости?
    

Если окажется, что доверительный интервал включает 0, то соответствующий коэффициент регрессии объявляется незначимым.

При заданном уровне значимости а = 0,05 и числе степеней свободы, равном n – 2, где n – заданный объем выборки (у нас n = 10) критическое значение статистики Стьюдента tкрит = 2,306.

27. 
    
    Как рассчитывается точечный прогноз результативной переменной?
    

Точечный прогноз результативной переменнойу на основе линейной модели парной регрессии при заданном значении факторной переменной хm будет осуществляться по формуле: ym=β0+β1xm+εm.

28. 
    Как рассчитали доверительные интервалы для прогноза результативной переменной? Что нужно рассчитать для нахождения доверительного интервала зависимой переменной?
    

[b1 – tкрит*S(b1);b1 + tкрит*S(b1)]; [b0 – tкрит*S(b0);b0 + tкрит*S(b0)].

29. 
    
    Какой интервал получится шире- 95% или 99%?
    

Шире 99%

30. 
    В чем различие между доверительными интервалами для оценки среднего и индивидуального значения результативного признака? Какой из этих интервалов получился шире, почему? Что еще влияет на ширину доверительного интервала результативного признака?
    

Различие в формулах S( y^ˆ_x* ) = S_E* S_E*

?Одинаковая ширина?

Расположение и ширина доверительных интервалов меняются от выборки к выборке. Действительно, их расположение и ширина зависят как от оценок коэффициентов, которые являются переменными (случайными величинами), так и от случайных значений выборочных оценок среднеквадратичных отклонений a и b.

31. 
    Что удалось доказать по результатам проверки значимости (ответ обосновать):
    
32. 
    
    Что такое автокорреляция в остатках? Как она влияет на результаты оценивания регрессионного уравнения?
    

Автокорреляция в остатках - корреляционная зависимость между значениями остатков zt за текущий и предыдущие моменты времени.

33. 
    
    Для чего используется статистика Дарбина-Уотсона?
    

Применяют для обнаружения автокорреляции, подчиняющейся авторегрессионному процессу 1-го порядка. Предполагается, что величина остатков еt в каждом t-м наблюдении не зависит от его значений во всех других наблюдениях.

34. 
    
    Какова нулевая гипотеза в тесте Дарбина-Уотсона?
    

Если коэффициент автокорреляции ρ положительный, то автокорреляция положительна, если ρ отрицательный, то автокорреляция отрицательна. Если ρ = 0, то автокорреляция отсутствует

35. 
    
    Какова альтернативная гипотеза в тесте Дарбина-Уотсона?
    

Альтернативные гипотезы и состоят, соответственно, в наличии положительной или отрицательной автокорреляции в остатках

36. 
    Нарисуйте числовую ось, которую использовали для формулировки решения в тесте Дарбина-Уотсона.
    

37. 
    
    Какой вывод сделали по результатам теста Дарбина-Уотсона?
    

Поскольку |tкрит| > tрасч, то нулевую гипотезу о равенстве нулю коэффициента корреляции отвергаем с вероятностью ошибки меньше 5% и делаем вывод о значимости коэффициента корреляции.

38. 
    
    Для чего проводили тест Голфелда-Квандта?
    

Оценить значимость уравнения регрессии. Пояснение: Тестирования гетероскедастичности случайных ошибок в регрессионной модели, которая применяется при существовании основания полагать, что может быть пропорционально стандартное отклонение ошибок некоторой переменной. 

39. 
    Что такое гомоскедастичность и гетероскедастичность остатков модели? Какое из этих свойств негативно сказывается на качество оценивания регрессионной модели?
    

Гетероскедастичность 
Случайной ошибкой называется отклонение в линейной модели множественной регрессии. Термин гетероскедастичность в широком смысле понимается как предположение о дисперсии случайных ошибок модели регрессии.

Гомоскедастичность

Гомоскедастичность остатков означает, что дисперсия каждого отклонения одинакова для всех значений x. Если это условие не соблюдается, то имеет место гетероскедастичность.

Гетероскедастичность остатков модели регрессии может привести к негативным последствиям:1) оценки неизвестных коэффициентов нормальной линейной модели регрессии являются несмещёнными и состоятельными, но при этом теряется свойство эффективности;2) существует большая вероятность того, что оценки стандартных ошибок коэффициентов модели регрессии будут рассчитаны неверно, что конечном итоге может привести к утверждению неверной гипотезы о значимости коэффициентов регрессии и значимости модели регрессии в целом.

40. 
    
    Какова нулевая гипотеза в тесте Голфелда-Квандта?
    

Нулевая гипотеза о гомоскедастичности остатков отвергается на 5%-ном уровне значимости.

41. 
    
    Какова альтернативная гипотеза в Голфелда-Квандта?
    

Гетероскедастичность - это свойство данных, используемых при построении регрессионной модели, когда разброс точек наблюдений вдоль линии регрессии является неравномерным на всем диапазоне изменения независимой переменной.

42. 
    
    Какой вывод сделали по результатам теста Голфелда-Квандта?
    

Принимая стандартный 5% уровень значимости, в таблице критических точек распределения Фишера находим Fкрит = F(0,05;1;8) = 5,32. Поскольку Fрасч = 28,6 превышает Fкрит = 5,32, то делаем вывод о значимости уравнения регрессии

43. 
    Что такое степень свободы для распределения? Какие значения степеней свободы использовали для нахождения табличного значения в F-критерии, t –критерии, тесте Дарбина-Уотсона, тесте Голфелда-Квандта?
    

Количество степеней свободы — это количество значений в итоговом вычислении статистики, способных варьироваться.

Значение – 8

44. 
    
    Что понимается под адекватностью модели?
    

Адекватность модели — совпадение свойств (функций/параметров/характеристик и т. п.) модели и соответствующих свойств моделируемого объекта

45. 
    
    С каких позиций исследуется адекватность линейной парной регрессии?
    

С позиции коэффициента детерминации – R^2

46. 
    
    Какой вывод по результатам проведенного анализа можете сделать об адекватности модели?
    

Коэффициент детерминации показывает, какую часть вариации (дисперсии) зависимой переменной Y воспроизводит (объясняет) построенное уравнение регрессии. В нашем случае построенное уравнение регрессии на 38,7% объясняет зависимость переменной Y от переменной X.

47. 
    
    Что характеризует коэффициент корреляции?
    

Коэффициент корреляции – это статистическая мера, которая вычисляет силу связи между относительными движениями двух переменных.

48. 
    
    Как меняется значение коэффициента корреляции при изменении ролей результативного признака и фактора?
    

с увеличением или с уменьшением значений одного признака происходит уменьшение или увеличение значений другого признака.

49. 
    
    Как на основе коэффициента корреляции делается вывод о тесноте и направлении связи между переменными?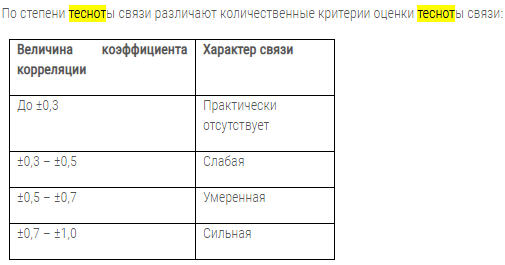
    

При отрицательной корреляции значения силы связи между переменными меняют на противоположные:

если величина коэффициента корреляции равна 0, следовательно переменные не связаны между собой;

если величина коэффициента корреляции между переменными равна 0,25 то это очень слабая корреляция и в большинстве случаев мы не берем ее в расчет;

если величина коэффициента корреляции между переменными равна 0, 75 то это высокая корреляция и в своих интерпретациях нам стоит обратить на нее внимание;

если величина коэффициента корреляции равна 1, следовательно полностью взаимосвязаны.

50. 
    
    Что означает значимость коэффициента корреляции?
    

51. 
    Какая статистика используется для проверки значимости коэффициента корреляции? Как формулируется нулевая и альтернативная гипотезы при проверке значимости коэффициента корреляции?
    

Для оценки значимости коэффициента корреляции следует использовать статистику

t = r_xy *

которая в условиях нулевой гипотезы H₀ : ρ_xy = 0