ПОЛУЧЕНИЕ МАТЕМАТИЧЕСКОЙ МОДЕЛИ ЭЛЕМЕНТОВ САР И ИХ ИССЛЕДОВАНИЕ С ПОМОЩЬЮ ЭВМ. ПОСТРОЕНИЕ ЧАСТОТНЫХ ХАРАКТЕРИСТИК. Мурзин Д.И. 13 вари пр.раб.. Лабораторная работа 1 "получение математической модели элементов сар и их исследование с помощью эвм. Построение частотных характеристик"
 Скачать 157.37 Kb. Скачать 157.37 Kb.
|
|
ЛАБОРАТОРНАЯ РАБОТА №1 "ПОЛУЧЕНИЕ МАТЕМАТИЧЕСКОЙ МОДЕЛИ ЭЛЕМЕНТОВ САР И ИХ ИССЛЕДОВАНИЕ С ПОМОЩЬЮ ЭВМ. ПОСТРОЕНИЕ ЧАСТОТНЫХ ХАРАКТЕРИСТИК" Цель работы: получение навыков построения математической модели элементов САР, ознакомление с понятием передаточной функции и построение частотных характеристик с использованием различных программ. 1 КРАТКИЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ 1.1 Математическое моделирование элементов САР. Одним из основных методов исследования САР и его элементов является моделирование. Моделирование – это исследование некоторого процесса при помощи модели. Моделью процесса является некоторый другой процесс, имеющий с данным процессом общие свойства, что позволяет использовать модель для изучения свойств моделируемого процесса. Наиболее широкое распространение в ТАУ при исследовании элементов САР используется математическое моделирование. Математическое моделирование – это метод изучения процессов и систем путем анализа их описания, выполненного на языке математики, т.е. их математической модели. Обычно для представления математической модели используется аналитическое описание, т.е. описание процессов в элементах с помощью уравнений, получаемых на основе физических, химических и других законов, которым подчиняются данные процессы, или экспериментально. Для линейных элементов и систем математическое аналитическое описание представляется совокупностью уравнений состояния системы (1.1) и уравнений связи (1.2): 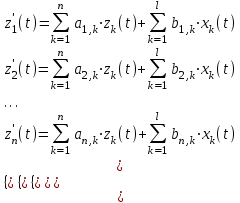 , (1.1) , (1.1)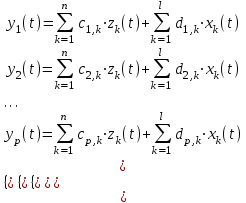 , (1.2) , (1.2)где 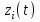 – переменные состояния системы, характеризующие ее параметры в момент времени t; – переменные состояния системы, характеризующие ее параметры в момент времени t; 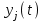 – выходные или управляемые параметры системы; – выходные или управляемые параметры системы;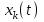 – внешние (входные) воздействия на систему, приводящие к изменению ее состояния; – внешние (входные) воздействия на систему, приводящие к изменению ее состояния; 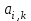 , , 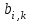 , , 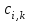 , , 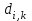 — постоянные коэффициенты. — постоянные коэффициенты. Система линейных дифференциальных уравнений состояния (1.1) совместно с уравнениями связи (1.2) исключением переменных состояния может быть представлена в виде системы из р линейных дифференциальных уравнений n-го порядка, непосредственно связывающих каждую выходную величину со всеми входными воздействиями. По отношению к одному входному воздействию x(t)=xk(t) каждое такое уравнение может быть представлено следующим образом: 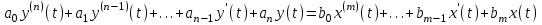 , (1.3) , (1.3)где 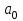 , …, , …, После того, как математическая модель получена, необходимо провести ее исследование, т.е. выяснить ее реакцию на различные типовые входные воздействия. Для исследования математических моделей САР в настоящее время широко используется моделирование на ЭВМ. 1.2 Передаточная функция линейных элементов САР. Линейными называются элементы, процессы в которых описываются линейными дифференциальными уравнениями. Любая линейная динамическая система в общем виде описывается уравнением (1.3). Применим к уравнению (1.3) интегральное преобразование Лапласа: 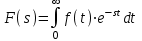 . (1.4) . (1.4)Данное преобразование устанавливает соответствие между функцией f(t) вещественного переменного t(при t 0) и функцией F(s) комплексного переменного s=+j (и – вещественные переменные; 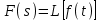 . .Таким образом, мы произведем переход в дифференциальном уравнении (1.3) от оригиналов y(t) и x(t) к соответствующим им изображениям Y(s) и X(s). Перед указанным переходом перечислим некоторые свойства преобразования Лапласа: 1) Линейность. Будем считать, что 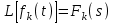 . .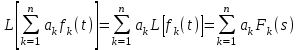 , (1.5) , (1.5)где 2) Дифференцирование оригинала. Для случая первой производной: 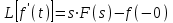 , (1.6) , (1.6)где f(-0) — значение оригинала при подходе к точке t = 0 слева. В случае n-ой производной: 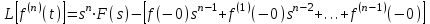 . (1.7) . (1.7)Если оригинал удовлетворяет условию f(t)=0 при t<0, то формулы (1.6), (1.7) упрощаются: 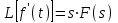 , (1.8) , (1.8)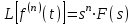 . (1.9) . (1.9)3) Интегрирование оригинала. 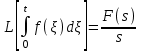 . (1.10) . (1.10)Ограничимся случаем, когда для (1.3) входное воздействие x(t)=0 при t<0, а система до момента t=0 находилась в состоянии покоя, т.е. y(-0) = y'(-0) = … = y(n-1)(-0)=0. Тогда согласно свойству дифференцирования оригинала (1.9) получаем следующее алгебраическое уравнение для изображений входной X(s) и выходной Y(s) величин системы: 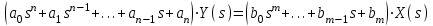 . (1.11) . (1.11)Перепишем (1.11) в следующем виде: 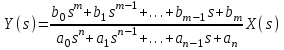 или введя обозначение 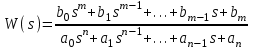 (1.12) (1.12)получим 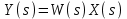 . (1.13) . (1.13)Функция комплексного переменного W(s) называется передаточной функцией системы. Передаточная функция – представляет собой отношение изображения выходного сигнала линейной САУ к изображению входного сигнала при нулевых начальных условиях. Данное определение следует из (1.13), поскольку согласно этой формуле: 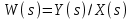 . (1.14) . (1.14)Смысл передаточной функции заключается в том, что она представляет собой некий оператор, преобразующий внешнее воздействие на входе в реакцию системы на выходе. 1.3 Частотные характеристики линейных элементов и систем. Приведем формулы, определяющие прямое преобразование Фурье, позволяющее для функции вещественной переменной (оригинала) f(t) найти ее Фурье-изображение F(j): 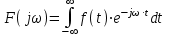 , (1.15) , (1.15)и обратное преобразование Фурье, дающее возможность по изображению найти оригинал: 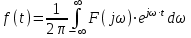 . (1.16) . (1.16)Изображение по Фурье F(j) функции f(t) еще называется комплексной спектральной плотностьюэтой функции, т.к. интеграл ее модуля |F(j)| в пределах двух произвольных частот 1 < < 2 равна сумме амплитуд всех гармоник разложения с частотами, расположенными в указанном диапазоне, с точностью до постоянного множителя 1/(2). Сопоставление прямого преобразования Лапласа (1.4) и Фурье (1.15) свидетельствует о том, что для "правосторонних" функций (т.е. удовлетворяющих условию f(t) = 0 при t < 0) эти преобразования совпадают, если считать s = j. Следовательно, для определения спектральной плотности выходной величины системы Y(j) можно воспользоваться формулой (1.13): 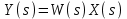 , ,заменив в ней sмнимой переменной j: 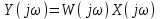 , (1.17) , (1.17)Комплексную функцию частоты W(j), получаемую из передаточной функции системы W(s) заменой s на j, называют комплексной частотной характеристикой(КЧХ) системы. КЧХ может быть представлена как в виде суммы ее вещественной (или действительной) и мнимой составляющих: 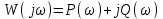 , (1.18) , (1.18)так и в показательном виде: 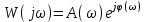 , (1.19) , (1.19)где А()и () – модуль и аргумент КЧХ, которые связаны с вещественной Р() и мнимой Q() частотными характеристиками соотношениями: 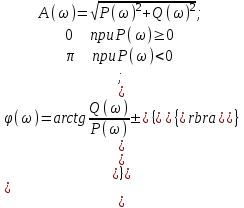 (1.20) (1.20)В выражении для ФЧХ, в случае когда Р()<0, «+» или «-» берется исходя из соображений, чтобы значение () по модулю было минимальным. Комплексная частотная характеристика системы W(j) являетсякомплексной функцией частоты,модуль которой есть ееамплитудная частотная характеристика А(),а аргумент – фазовая частотная характеристика (). Амплитудная частотная характеристикасистемы (АЧХ) показывает зависимость от частоты отношения амплитуд колебаний на выходе и входе, а фазовая частотная характеристика(ФЧХ) – сдвига по фазе. График КЧХ построенный в комплексной плоскости для частот входного сигнала 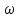 от 0 до от 0 до 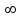 называется годографом (рис.1.1). называется годографом (рис.1.1).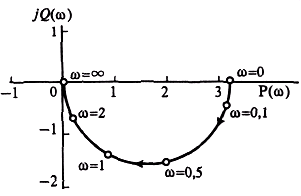 Рис.1.1. График КЧХ (годограф). 2 ЗАДАНИЕ И ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ 2.1. Студенту необходимо выполнить исследование частотных характеристик элемента (динамического звена) САР заданного с помощью одной из электрических принципиальных схем, изображенных на рис.1.1. Номер рисунка схемы и номиналы значений элементов схемы берутся из табл. 1.1 согласно варианту, выданному преподавателем. Таблица 1.1
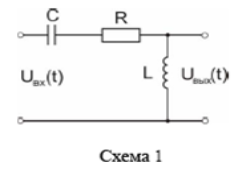 Рис.1.1. Электрическая принципиальная схема элементов САР (динамических звеньев). 2.2 Для заданной схемы необходимо составить систему дифференциальных уравнений, описывающих его поведение при различных входных воздействиях. На основе полученной системы вывести дифференциальное уравнение относительно входного воздействия Uвх(t) и выходного сигнала Uвых(t). 2.3 Выполнить переход от дифференциального уравнения к передаточной функции исследуемого звена. 2.4 По передаточной функции построить аналитические выражения частотных характеристик динамического звена: комплексную частотную характеристику (КЧХ), амплитудную частотную характеристику (АЧХ) и фазовую частотную характеристику (ФЧХ). 2.5 С помощью программ MathCad и MultiSim (приложение пакета программ LabView) построить графики КЧХ, АЧХ, ФЧХ. 2.6 Оформить отчет и защитить работу. 3 РАСЧЁТНАЯ ЧАСТЬ 3.1 Например, дано динамическое звено, электрическая принципиальная схема которого показана на рис.1.2.  Рис.1.2. Электрическая принципиальная схема исследуемого звена. Необходимо определить передаточную функцию и частотные характеристики этого звена. 3.2 Получим систему дифференциальных уравнений, описывающих поведение звена, т.е. построим его математическую модель. Для этого воспользуемся вторым законом Кирхгоффа: 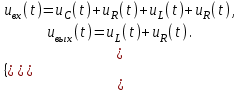 Используем закон Ома для участка цепи 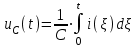 , , 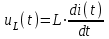 , , 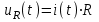 , , получаем систему дифференциальных уравнений: 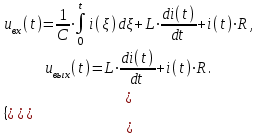 Применим к полученным уравнениям прямое преобразование Лапласа (свойства преобразования Лапласа (1.5), (1.8) и (1.10)), в результате чего получим систему операторных уравнений: 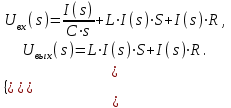 При нулевых нормальных условиях получим передаточную функцию: 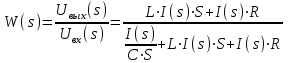 , разделим все слагаемые на I(s): , разделим все слагаемые на I(s):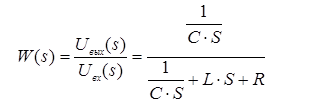 (1.21) 3.3 Перейдем к построению частотных характеристик звена. Выполнив в полученной передаточной функции замену s на j, где j = 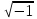 , а -циклическая частота. , а -циклическая частота.Получим выражение для КЧХ: . (1.22) 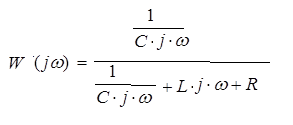 4 ИССЛЕДОВАНИЕ ЧАСТОТНЫХ СВОЙСТВ ЗВЕНА С ПОМОЩЬЮ СПЕЦИАЛИЗИРОВАННЫХ ПРОГРАММ 4.1 Построим частотные характеристики исследуемого звена в среде программы MathCAD для динамического звена, схема которого показана на рис.1.2, имеющего параметры R = 0.5 Ом, L = 60 Гн, C = 70 мкФ. 4.1.1 Запустите программу MathCAD. 4.1.2 В появившемся рабочем листе введите параметры вашего звена, значение мнимой единицы j и вид КЧХ (рис.1.3).  Рис.1.3. Фрагмент начала программы в среде MathCAD. 4.1.3 С помощью функций Re() и Im(), встроенных в MathCAD определим действительную P() и мнимую Q() частотную характеристики. После чего, задав параметры дискретного аргумента , в шаблоне декартового графика (X-Y Plot) построим годограф КЧХ (рис.1.4). 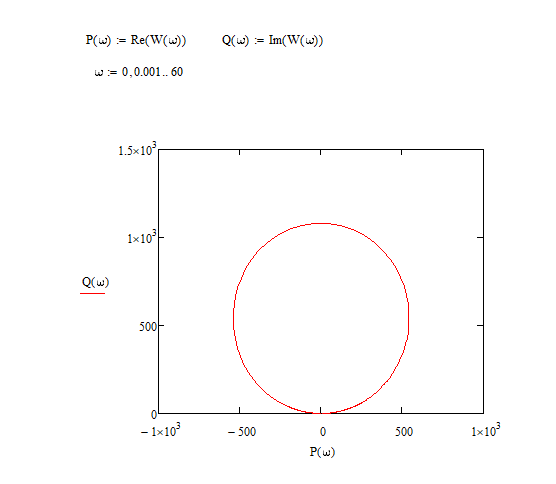 Рис.1.4. Построение годографа КЧХ в среде MathCAD. Этот и последующие фрагменты программы размещаются на рабочем листе MathCAD один под другим. 4.1.4 Пользуясь первой формулой (1.20) зададим вид и построим график АЧХ (рис.1.5). 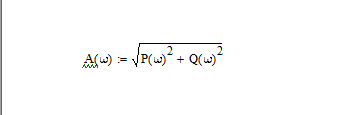 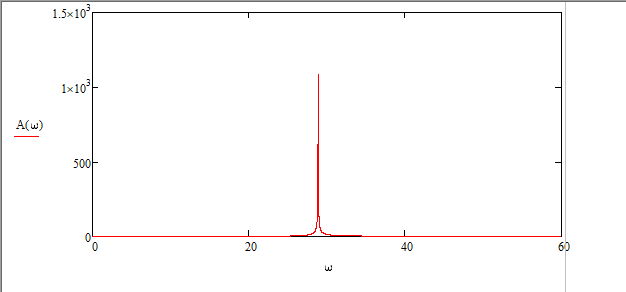 Рис.1.5. Построение графика АЧХ в среде MathCAD. 4.1.5 В соответствии со вторым выражением (1.20), записываем функцию для ФЧХ. Перед этим посмотрим на график КЧХ (рис.1.4) и установим, принимает ли P() отрицательное значение при тех или иных значениях . Если P() принимает положительные значения при любых значениях , то ФЧХ можно представить выражением: 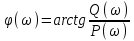 . .Если P() принимает отрицательные значения при некоторых значениях , то выражение для ФЧХ необходимо дополнить выражением, которое учитывает смену знака P(). В нашем примере P() может принимать отрицательные значения, поэтому на листе MathCAD запишем выражение ФЧХ и построим ее график, как показано на рис.1.6. 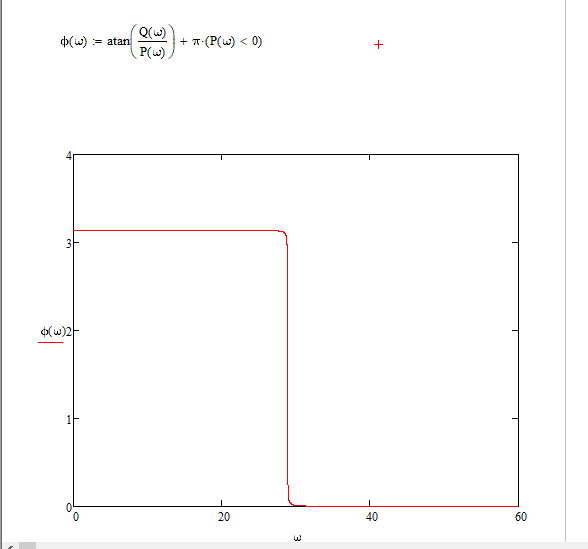 Рис.1.6. Построение графика ФЧХ в среде MathCAD. Знак «+» или «-» в выражении на рис.1.6. выбирается из соображений, чтобы значение () по модулю было минимальным. Добавьте два декартовых графика, отражающих зависимость АЧХ и ФЧХ от частоты f=/(2) (рис.1.7). 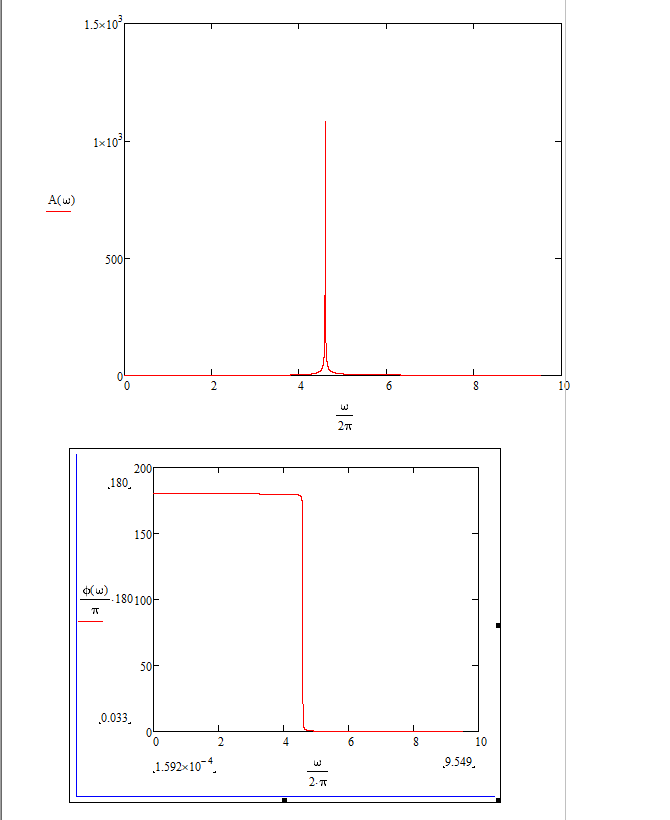 Рис.1.7. Построение зависимостей АЧХ и ФЧХ от частоты f Вывод: Получил навыки построения математической модели элементов САР, ознакомился с понятием передаточной функции и построение частотных характеристик с использованием MathCAD. В среде MathCAD мы делали необходимый расчет для нахождения коэффициентов W(s). |
