Лабораторная работа 1 разветвляющийся вычислительный процесс Задания варианта Задача 1
 Скачать 108 Kb. Скачать 108 Kb.
|
|
Лабораторная работа №1 «РАЗВЕТВЛЯЮЩИЙСЯ ВЫЧИСЛИТЕЛЬНЫЙ ПРОЦЕСС» Таблица 1 – Задания
Тексты задач 44. Если сумма трех попарно различных действительных чисел X, Y, Z меньше единицы, то наименьшее из этих чисел заменить полусуммой двух других; в противном случае заменить меньшее из X и Y полусуммой двух оставшихся значений. 45. Даны действительные числа A,B,C,D. Если A<=B<=C<=D, то каждое число заменить наибольшим из них; если A>B>C>D, то числа оставить без изменения; в противном случае все числа заменяются их квадратами. 46. Даны действительные числа Х, Y. Если оба числа отрицательны, то каждое число заменить его модулем; если отрицательное только одно из них, то оба значения увеличить на 0.5; если оба числа положительны и ни одно из них не принадлежит отрезку [ 0.5, 2.0 ], то оба значения уменьшить в 10 раз; в остальных случаях числа оставить без изменения. 47. Заданы действительные положительные числа X, Y, Z. а) Выяснить существует ли треугольник с длинами сторон Х, Y, Z. б) Если треугольник существует, то ответить - является ли он остроугольным. 5 0. Даны действительные числа A1,B1,C1,A2,B2,C2. Выяснить, верно ли, что И если верно, то найти решение системы линейных уравнений A 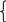 1*X + B1*Y + C1 = 0 1*X + B1*Y + C1 = 0A2*X + B2*Y + C2 = 0 (при выполнении написанного неравенства система заведомо совместна и имеет единственное решение). 51. Даны действительные числа A, B, C (A<>0). Полностью исследовать биквадратное уравнение A*X4+ B*X2 + C = 0, то есть если действительных корней нет, то должно быть выдано соответствующее сообщение, иначе должны быть выданы значения двух или четырех корней. 52. Даны действительные числа A, B, C, D, S, T, U ( S и T одновременно не равны нулю). Известно, что точки (A,B) и (C,D) не лежат на прямой L, заданной уравнением S*X + T*Y + U = 0. Прямая L разбивает координатную плоскость на две полуплоскости. Выяснить, верно ли, что точки (A,B) и (C,D) принадлежат разным полуплоскостям. Примечание. Две точки (A,B) и (C,D), не лежащие на одной прямой, определяемой уравнением S*X + T*Y + U = 0, принадлежат одной полуплоскости, если S*A + T*B + U и S*C + T*D + U - числа одного знака. 53. Даны действительные числа A,B,C,D,E,F,G,H. Известно, что точки (E,F) и (GH) различны. Известно также, что точки (A,B) и (C,D) не лежат на прямой L проходящей через точки (E,F) и (G,H). Прямая L разбивает координатную плоскость на две полуплоскости. Выяснить, верно ли, что точки (A,B) и (C,D) принадлежат одной и той же полуплоскости. Примечание. Уравнение прямой, проходящей через две точки (E,F) и(G,H): (X-E)*(H-F)-(Y-F)*(G-E)=0. 54. Даны действительные числа X1, X2, X3, Y1, Y2, Y3. Принадлежит ли начало координат треугольнику с вершинами (X1,Y1), (X2,Y2), (X3,Y3) ? 55. Даны действительные положительные числа A, B, C, D. Выяснить, можно ли прямоугольник со сторонами A, B уместить внутри прямоугольника со сторонами C, D так, чтобы каждая из сторон одного прямоугольника была параллельна каждой стороне второго прямоугольника. 56. Даны действительные положительные числа A, B, C, X, Y. Выяснить, пройдет ли кирпич с ребрами A, B, C в прямоугольное отверстие со сторонами X,Y. Просовывать кирпич в отверстие разрешается только так, чтобы каждое из его ребер было параллельно или перпендикулярно каждой из сторон отверстия. 58. Дано действительное число A. Для функций, графики которых представлены на рисунке 1 вычислить значения F(A). 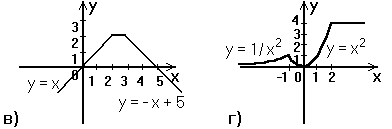 Рисунок 1 59. Заданы действительные числа X и Y. Определить, принадлежит ли точка с координатами (X,Y) заштрихованной части плоскости.(см. рис. 2). 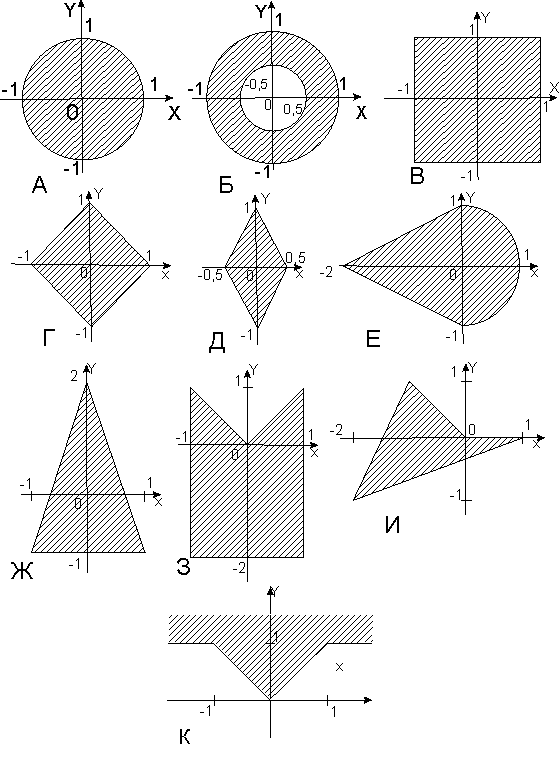 Рисунок 2 60. Пусть D - заштрихованная часть плоскости (см. рис. 3) и пусть задана точка своими координатами (X,Y). Запись (X,Y) D означает, что точка с координатами X, Y лежит внутри заштрихованной области D. Определить значение функции U следующим образом: 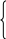 0, если (X,Y) D, 0, если (X,Y) D,a) U = X, в противном случае 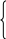 -3, если (X,Y) D, б) U = Y2, в противном случае 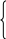 X-Y, если (X,Y) D, X-Y, если (X,Y) D,в) U = X*Y, в противном случае 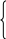 X2-1, если (X,Y) D, X2-1, если (X,Y) D,г) U = I X-1 I, в противном случае 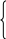 I X2-1 I, если (X,Y) D, I X2-1 I, если (X,Y) D,д) U = X+Y, в противном случае 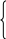 X+Y, если (X,Y) D, X+Y, если (X,Y) D,е) U = X-Y, в противном случае  Рисунок 3 Пример выполнения лабораторной работы по теме "Разветвляющийся вычислительный процесс" 1. Условие задачи Если три отрезка x, y, z образуют треугольник, то проверить, является ли он прямоугольным и вывести сообщение об этом, в противном случае (треугольник не прямоугольный) найти периметр треугольника и площадь. Введем следующие обозначения: Pr - периметр, S - площадь. 2. Математическая модель Используем следующие математические положения и формулы: 1. В треугольнике сумма длин двух любых его сторон больше третьей. 2. По теореме Пифагора в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов. 3. Для вычисления площади треугольника применим формулу Герона периметр Pr = x + y + z площадь по формуле Герона S =(p (p-x) (p-y) (p-z))1/2, где p-полупериметр 3. Таблица 1 – Внешние спецификации
Таблица сообщений C1.1: “Треугольник существует” C1.2: “Треугольник не существует” C2.1: “он прямоугольный” C2.2: “только не прямоугольный” C3.1: ' периметр треугольника =' C3.2: ' площадь треугольника =' 4.Алгоритмизация Блок-схема алгоритма (допускается словесное описание алгоритма) представлена на рис. 1. 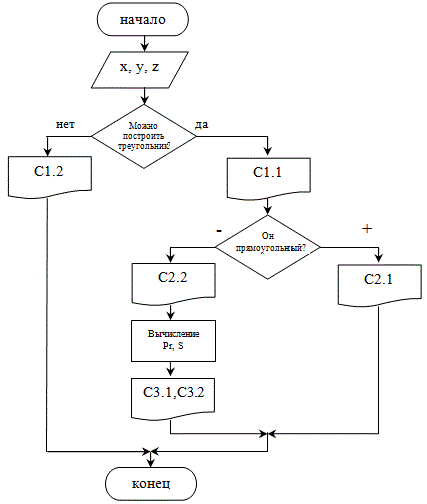 Рисунок 1 – Блок-схема алгоритма 5. Проектирование тестов Таблица 2 – Таблица тестов
6. Проверка правильности алгоритма с помощью таблицы тестов (только для работы №1) Тест 1,2: блоки 1,2,3,4,11 Тест 3: блоки 1,2,3,5,6,10,11 Тест 4: блоки 1,2,3,5,6,7,8,9,11 7. Кодирование алгоритма или запись алгоритма на языке С++ // пример лабораторной работы #1 #include #include using namespace std; int main() { setlocale(LC_ALL, "Russian"); float x,y,z; float S,Pr,p; cout << "Введите длины сторон трегольника" << endl; cin >> x >>y >>z; //проверяем существование треугольника if ((x>0)&&(y>0)&&(z>0)&&(x+y>z)&&(y+z>x)&&(x+z>y)) { cout << "Треугольник существует" << endl; //проверяем по теореме Пифагора, является ли треугольник прямоугольным if (fabs( x*x - y*y - z*z )==0 || fabs(z*z - y*y - x*x)==0 || fabs(y*y - z*z - x*x)==0) cout << "Треугольник прямоугольный" << endl; else { cout << "Треугольник не прямоугольный" << endl; Pr= x + y + z; p=Pr/2; cout << "Полупериметр треугольника = " < S= sqrt (p* (p-x) * (p- y) * (p- z)); cout << "Площадь треугольника = " < } } else cout << "Треугольник не существует" << endl; return 0; } | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
