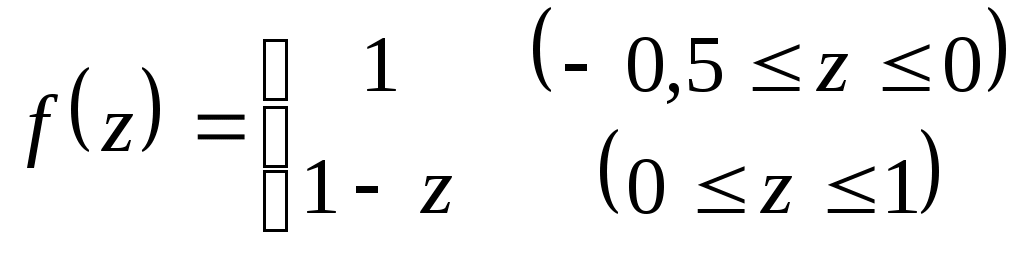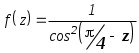Лабораторная работа 1 Реализация нелинейной нестационарной модели

• Название: Лабораторная работа 1 Реализация нелинейной нестационарной модели
• Дата: 05.10.2021
• Размер: 298 Kb.
• Имя файла: 1,2,3,4,5,6,7,8.doc
• Тип: Лабораторная работа; #241707

Лабораторная работа №1

Реализация нелинейной нестационарной модели
Нелинейная нестационарная модель задана в виде дифференциальных уравнений.

Требуется:

1. Рассчитать процесс до t₁=10c¹.

2. Найти искомый параметр (указан в задании, например Х₄(t₁)) с относительной погрешностью 1% методом Эйлера, используя половинное деления шага интегрирования. Для этого обязательно, требуется проанализировать зависимость погрешности от шага. Также, оцените трудоемкость,² требуемую для получения искомого параметра с заданной точностью.
Для выполнения работы необходимо сделать программу и отчет в электронном виде.

В отчете д.б.:

- зависимости фазовых переменных переменных ({X_i}, i=1,2…) от времени,

- зависимость погрешности от шага интегрирования,

- значение искомого параметра, шага интегрирования при котором он найден и затраченную на поиск трудоемкость.

Лабораторная работа №2

Построить имитационную модель детерминированного конечного автомата

Номер варианта	Тип автомата	Количество входов	Количество состояний	Количество выходов
1	Мили	3	3	3
2	Мура	3	5	3
3	Автономный	--	6	4
4	Мура	4	4	2
5	Без памяти	10	--	8
6	Мили	2	3	3
7	Мили	3	4	2
8	Мура	3	4	3
9	Мили	2	4	3
10	Автономный	--	8	3
11	Без памяти	12	--	5
12	Мура	5	3	2
13	Мили	4	3	2
14	Без выхода	4	4	--
15	Автономный	--	7	5
16	Мура	3	6	2
17	Мили	3	3	4
18	Без памяти	13	--	7
19	Мили	4	3	5
20	Мура	3	4	2
21	Мура	2	5	4
22	Мили	2	4	2
23	Мили	3	3	4
24	Мура	5	4	3
25	Без выхода	3	5	--

Для выполнения работы требуется сделать программу и отчет в электронном виде. При выполнении работы отобразить на экране результаты моделирования (переменные модели от времени).

Лабораторная работа №3

Построение генератора случайных чисел

1. Построить программный генератор случайных чисел с заданным законом распределения. Рекомендуется использовать метод обратных функций.

2. Оценить величину математического ожидания и дисперсии по выборкам объемом 50, 100, 1000, 10⁵ и сравнить с точными величинами, полученными аналитически.

3. Для выборок указанных в п.2., оценить соответствие полученного закона заданному, используя указанный критерий согласия: Пирсона (1) или Колмогорова (2).

В случае применения критерия Пирсона, предусмотреть построение гистограммы

В случае применения критерия Колмогорова, предусмотреть построение выборочной функции распределения.

Варианты задания:

№ вар	Плотность распределения вероятностей и интервал распределения	Критерий согласия	№ вар	Плотность распределения вероятностей и интервал распределения	Критерий согласия
1		1	13		2
2		2	14		1
3		1	15		2
4		1	16		1
5		2	17		1
6		2	18		2
7		1	19		1
8		2	20		2
9		1	21		2
10		2	22		1
11		2	23		1
12		1	24		1

Лабораторная работа №4

Построение генератора случайного процесса

Построить программный генератор непрерывного случайного процесса с заданной корреляционной функцией . Использовать метод формирующего фильтра. Значения дисперсии D, параметра и шага дискретизации h заданы в таблице вариантов.

Рассчитать и построить графики заданной и полученной корреляционных функций для интервала .

№ варианта	D		h
1	0.2	3	0.01
2	2	5	0.001
3	5	1	0.001
4	1	2	0.001
5	0.1	10	0.001
6	1	0.1	0.01
7	2	5	0.001
8	0.5	2	0.001
9	2	4	0.001
10	0.1	5	0.001
11	1	0.5	0.01
12	4	0.2	0.01
13	3	5	0.001
14	1	4	0.001
15	0.1	0.1	0.01
16	1	1	0.01
17	2	2	0.001
18	1	10	0.001
19	5	0.2	0.01
20	0.1	2	0.001
21	0.4	1	0.001
22	1	1	0.001
23	2	0.2	0.01
24	1	2	0.001
25	0.5	5	0.001

Лабораторная работа №5

Построить программный генератор непрерывного случайного процесса с заданной корреляционной функцией и законом распределения.

Корреляционную функцию взять из четверной, функцию распределения из третьей лабораторной работы.

При выполнении каждого этапа работы предусмотреть вывод необходимых переменных и графиков.

Проверка соответствия заданной и полученной ФРВ производится методом Колмогорова или Пирсона.

Лабораторная работа №6

Проверить стационарность и эргодичность случайного процесса полученного в пятой лабораторной работе. Использовать метод Смирнова-Колмогорова.

Лабораторная работа №7

Моделирование одноканальной СМО с отказами

Построить имитационную статистическую модель одноканальной системы массового обслуживания с отказами. Процесс смены состояний системы считать марковским, поток заявок - простейшим. Интенсивность потока заявок  и производительность канала  заданы в таблице вариантов.

На основе построенной модели получить оценку для установившегося процесса указанной в таблице вариантов характеристики системы x, наблюдая процесс в течение 100с. Оценить точность результата.

Определить требуемое время наблюдения процесса для оценки искомой характеристики с абсолютной погрешностью не более 0,01. Получить такую оценку.

Для проверки результатов получить значение искомой характеристики аналитическим методом.

№ варианта , с-1 , с-1 x 1 0.5 0.3 p 2 1 0.5 св 3 20 5 p1 4 2.5 0.5 q 5 1 0.6 k 6 25 10 p0 7 0.1 0.2 зн 8 1 1.5 p 9 10 2 q 10 10 10 p 11 12 6 q 12 20 10 q

№ варианта , с-1 , с-1 x 13 0.1 0.01 св 14 0.2 0.08 p1 15 30 10 q 16 0,2 0,05 св 17 10 20 p 18 1 2 p1 19 5 1 св 20 2 1 k 21 1 2 св 22 5 10 зн 23 1.5 0.5 q

Условные обозначения:

p₀, p₁ - вероятности состояний системы,

p - вероятность обслуживания заявки,

q - вероятность отказа в обслуживании,

_св - средняя доля времени пребывания канала в нерабочем состоянии,

_зн - средняя доля времени пребывания канала в рабочем состоянии,

k - среднее число занятых каналов.

Лабораторная работа №8

Моделирование многоканальной СМО с ограниченной очередью

Построить имитационную статистическую модель n-канальной системы массового обслуживания с очередью на m заявок. Процесс смены состояний системы считать марковским, поток заявок - простейшим. Интенсивность потока заявок  и производительность канала  соответствуют варианту задания 7. Значения n и m указаны в таблице вариантов.

На основе построенной модели получить оценку для установившегося процесса указанной в таблице вариантов характеристики системы x, наблюдая процесс в течение 100с. Оценить точность результата.

Определить требуемое время наблюдения процесса для оценки искомой характеристики с абсолютной погрешностью не более 0,01. Получить такую оценку.

Для проверки результатов получить значение искомой характеристики аналитическим методом.

№ варианта	n	m	x	№ варианта	n	m	x
1	3	1	k	1	2	2	q
2	3	1	p	2	3	1	p
3	2	2	q	3	2	2	q
4	2	2	k	4	3	1	k
5	3	1	p	5	2	2	p
6	2	2	p	6	2	2	k
7	2	2	q	7	2	2	p
8	3	1	p	8	2	2	k
9	3	1	k	9	2	2	k
10	2	2	k	10	3	1	p
11	2	2	p	11	3	1	q
12	3	1	q	12	2	2	q
13	2	2	k	13	3	1	k
14	2	2	q	14	2	2	q
15	3	1	p	15	2	2	p
16	2	2	q	16	3	1	q
17	3	1	k	17	3	1	k
18	2	2	q	18	2	2	p
19	3	1	p	19	3	1	p
20	3	1	q	20	3	1	q
21	2	2	k	21	2	2	k
22	2	2	q	22	3	1	q
23	3	1	p	23	2	2	k
24	2	2	p	24	3	1	q
25	2	2	k	25	3	1	p

Условные обозначения:

p - вероятность обслуживания заявки,

q - вероятность отказа в обслуживании,

k - среднее число занятых каналов.

1 т.е. построить все необходимые зависимости (хотя бы переменные Х от времени)

2 кол-во итераций интегрирования модели