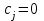Лабораторная работа №1 Решение логических задач. Лабораторная работа 1 Решение логических задач Цель работы
 Скачать 454.13 Kb. Скачать 454.13 Kb.
|
Контрольные вопросыЧто строится в процессе календарного планирования? Что определяется в процессе календарного планирования? В чем назначение календарного планирования? Опишите задачу С. Джонсона для двух станков. Опишите задачу распределения заказов. Лабораторная работа №8 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Ресурсы | Нормы затрат ресурсов на одно изделие | Общее количество ресурсов | |
| стол | шкаф | ||
| Древесина 1 вида | 0,2 | 0,1 | 40 |
| Древесина 2 вида | 0,1 | 0,3 | 60 |
| Трудоемкость (человеко-часов) | 1,2 | 1,5 | 371,4 |
| Прибыль от реализации одного изделия (руб.) | 6 | 8 | |
Определить, сколько столов и шкафов фабрике следует изготовлять, чтобы прибыль от их реализации была максимальной.
Решение
Для решения этой задачи необходимо построить математическую модель. Процесс построения модели можно начать с ответа на следующие три вопроса:
Для определения каких величин строится модель?
В чем состоит цель, для достижения которой из множества всех допустимых значений переменных выбираются оптимальные?
Каким ограничениям должны удовлетворять неизвестные?
В данном случае мебельной фабрике необходимо спланировать объем производства столов и шкафов так, чтобы максимизировать прибыль. Поэтому переменными являются: х1 - количество столов, х2 - количество шкафов
Суммарная прибыль от производства столов и шкафов равна z=6*x1+8*x2. Целью фабрики является определение среди всех допустимых значений х1 и х2 таких, которые максимизируют суммарную прибыль, т.е. целевую функцию z
Ограничения, которые налагаются на х1 и х2:
объем производства шкафов и столов не может быть отрицательным, следовательно: х1, х2 0.
нормы затрат древесины на столы и шкафы не может превосходить максимально возможный запас данного исходного продукта, следовательно:
0,2x1+ 0,1x2 40,
0,1x1 +0,3x2 60.
Кроме того, ограничение на трудоемкость не превышает количества затрачиваемых ресурсов
1,2x1+ 1,5х2 371,4.
Таким образом, математическая модель данной задачи имеет следующий вид:
Максимизировать функции.
z = 6х1 + 8х2
при следующих ограничениях:
0,2x1+ 0,1x2 40
0,1x1 +0,3x2 60
1,2x1+ 1,5х2 371,4
Данная модель является линейной, т.к. целевая функция и ограничения линейно зависят от переменных.
Решение задачи с помощью MSExcel
1. Отвести ячейки A3 и ВЗ под значения переменных х1 и х2 (рис. 8.1).
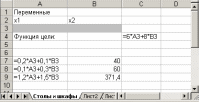
Рис.8.1. Диапазоны, отведенные под переменные,
целевую функцию и ограничения
2. В ячейку С4 ввести функцию цели: =6*АЗ+8*ВЗ, в ячейки А7:А9 ввести левые части ограничений:
=0,2*А3+0,1*ВЗ
=0,1*А3+0,3*ВЗ
= 1,2*АЗ+1,5*ВЗ,
а в ячейки В7:В9 - правые части ограничений. (рис.8.1.)
3. Выбрать команды Сервис/Поиск_решения'>Сервис/Поиск решения (Tools/Solver) и заполнить открывшееся диалоговое окно Поиск решения (Solver) как показано на рис 8.2. Средство поиска решений является одной из надстроек Excel. Если в меню Сервис (Тоо1з) отсутствует команда Поиск решения (Solver), то для ее установки необходимо выполнить команду Сервис/ Надстройки/ Поиск решения (Tools/Add-ins/Solver). Для ввода ограничений нажмите кнопку Добавить.
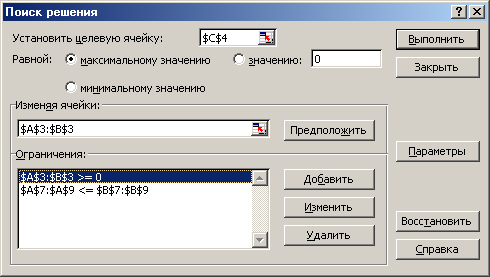
Рис. 8.2. Диалоговое окно Поиск решения задачи о максимизации прибыли на фабрике
Внимание! В диалоговом окне Параметры поиска решения (Solver Options) необходимо установить флажок Линейная модель (Assume Linear Model) (Рис.8.3.).
Рис.8.3. Диалоговое окно Параметры поиска решения
4. После нажатия кнопки Выполнить (Solve) открывается окно Результаты поиска решения (Solver Results), которое сообщает, что решение найдено (рис. 8.4).
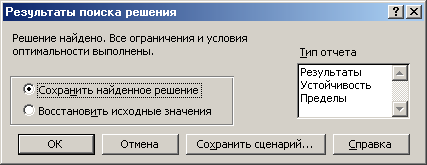
Рис. 8.4. Диалоговое окно Результаты поиска решения
5. Результаты расчета задачи представлены на рис. 8.5, из которого видно, что оптимальным является производство 102 столов и 166 шкафов. Этот объем производства принесет фабрике 1940 руб. прибыли.
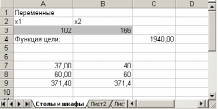
Рис.8.5. Результаты расчета с помощью средства поиска решений для задачи максимизации выпуска столов и шкафов
Индивидуальное задание
Построить математическую модель задачи, согласно вашему варианту.
Решить задачу с помощью средства MS Excel Поиск решения.
Сделать соответствующие выводы.
Вариант 1
Для производства двух видов изделий А и В используется токарное, фрезерное и шлифовальное оборудование. Нормы затрат времени для каждого из типов оборудования на одно изделие данного вида приведены в табл.8.2. В ней же указан общий фонд рабочего времени каждого из типов оборудования, а также прибыль от реализации одного изделия.
Таблица 8.2
| Тип оборудования | Затраты времени (станко-часов) на обработку одного изделия | Общий фонд полезного рабочего времени | |
| А | В | ||
| Фрезерное Токарное Шлифовальное | 10 5 6 | 8 10 12 | 168 180 144 |
| Прибыль от реализации одного изделия (руб.) | 14 | 18 | |
Найти план выпуска изделий вида А и В, обеспечивающий максимальную прибыль от их реализации.
Вариант 2
На звероферме могут выращиваться черно-бурые лисицы и песцы. Для обеспечения нормальных условий их выращивания используется три вида кормов. Количество корма каждого вида, которое должны ежедневно получать лисицы и песцы, приведено в табл.8.3. В ней же указаны общее количество корма каждого вида, которое может быть использовано зверофермой, и прибыль от реализации одной шкурки лисицы и песца.
Найти оптимальное соотношение количества кормов и численности поголовья лис и песцов.
Таблица 8.3
| Вид корма | Количество единиц корма, которое ежедневно должны получать | Общее количество корма | ||
| А | В | |||
| Вид 1 Вид 2 Вид 3 | 2 4 6 | 3 1 7 | 180 240 426 | |
| Прибыль от реализации одной шкурки (руб.) | 16 | 12 | | |
Вариант 3
Для изготовления различных изделий А, В и С предприятие использует три различных видов сырья Нормы расхода сырья на производство одного изделия каждого вида, цена одного изделия А, В и С, а также общее количество сырья каждого вида, которое может быть использовано предприятием, приведены в табл. 8.4.
Таблица 8.4
| Вид сырья | Норма затрат сырья (кг) на одно изделие | Общее количество сырья (кг) | ||
| А | В | С | ||
| Вид 1 | 18 | 15 | 12 | 360 |
| Вид 2 | 6 | 4 | 8 | 192 |
| Вид 3 | 5 | 3 | 3 | 180 |
| Цена одного изделия (руб.) | 9 | 10 | 16 | |
Изделия А, В и С могут производится в любых соотношениях (сбыт обеспечен), но производство ограничено выделенным предприятию сырьем каждого вида.
Составить план производства изделий, при котором общая стоимость всей произведенной предприятием продукции является максимальной.
Вариант 4
На швейной фабрике для изготовления четырех видов изделий может быть использована ткань трех артикулов. Нормы расхода тканей всех артикулов на пошив одного изделия приведены в табл.8.5. В ней же указаны имеющиеся в распоряжении фабрики общее количество тканей каждого артикула и цена одного изделия данного вида. Определить, сколько изделий каждого вида должна произвести фабрика, чтобы стоимость изготовленной продукции была максимальной.
Таблица 8.5
| Артикул ткани | Норма расхода ткани (м) на одно изделие вида | Общее количество ткани (м) | |||
| Вид 1 | Вид 2 | Вид 3 | Вид 4 | ||
| Артикул 1 | 1 | - | 2 | 1 | 180 |
| Артикул 2 | - | 1 | 3 | 2 | 210 |
| Артикул 3 | 4 | 2 | - | 4 | 800 |
| Цена одного изделия (руб.) | 9 | 6 | 4 | 7 | |

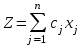 при линейных ограничениях
при линейных ограничениях 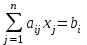
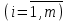 . Необходимым условием экстремума является
. Необходимым условием экстремума является 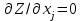
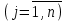 . Но
. Но 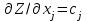 . Отсюда
. Отсюда