Лабораторная работа №1 Решение логических задач. Лабораторная работа 1 Решение логических задач Цель работы

• Название: Лабораторная работа 1 Решение логических задач Цель работы
• Дата: 30.11.2021
• Размер: 454.13 Kb.
• Имя файла: Лабораторная работа №1 Решение логических задач.docx
• Тип: Лабораторная работа; #287251
• страница: 6 из 21

Индивидуальное задание

Решите задачу, согласно вашему индивидуальному варианту.

Вариант 1

Найти наилучшие стратегии по критериям: Вальда, Сэвиджа, Гурвица (коэффициент пессимизма равен 0,2), Гурвица применительно к матрице рисков (коэффициент пессимизма равен 0,4) для следующей платежной матрицы игры с природой (элементы матрицы - выигрыши):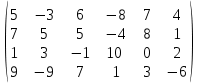

Вариант 2

Дана матрица игры с природой в условиях полной неопределенности (элементы матрицы - выигрыши):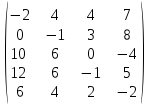


Требуется: проанализировать оптимальные стратегии игрока, используя критерии пессимизма-оптимизма Гурвица применительно к платежной матрице А и матрице рисков R при коэффициенте пессимизма р = 0; 0,5; 1. При этом выделить критерии максимакса, Вальда и Сэвиджа.

Вариант 3

Дана следующая матрица выигрышей: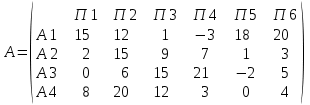

Определите оптимальную стратегию используя критерии Вальда, Сэвиджа и Гурвица (коэффициент пессимизма равен 0,4).

Вариант 4

Один из пяти станков должен быть выбран для изготовления партии изделий, размер которой Q может принимать три значения: 150, 200, 350. Производственные затраты Сi для I станка задаются следующей формулой:

Ci = Pi + ci*Q

Данные Pi и ci приведены в табл4.2.

Таблица 4.2

Показатели	Модель станка
	1	2	3	4	5
Pi	30	80	50	160	100
ci	14	6	10	5	4

Решите задачу для каждого из следующих критериев Вальда, Сэвиджа, Гурвица (критерий пессимизма равен 0,6). Полученные решения сравните.

Вариант 5

При выборе стратегии Aj по каждому возможному состоянию природы Si соответствует один результат Vij. Элементы Vij являющиеся мерой потерь при принятии решения, приведены в табл. 4.3.

Таблица 4.3

Стратегии	Состояние природы
	S1	S2	S3	S4
A1	2	6	5	8
A2	3	9	1	4
A3	5	1	6	2

Выберите оптимальное решение в соответствии с критериями Вальда, Сэвиджа, Гурвица (при коэффициенте пессимизма равном 0,5).

Вариант 6

Намечается крупномасштабное производство легковых автомобилей. Имеются четыре варианта проекта автомобиля Rj. Определена экономическая эффективность Vji каждого проекта в зависимости от рентабельности производства. По истечении трех сроков Si рассматриваются как некоторые состояния среды (природы). Значения экономической эффективности для различных проектов и состояний природы приведены в табл. 4.4.

Таблица 4.4

Проекты	Состояние природы
	S1	S2	S3
R1	20	25	15
R2	25	24	10
R3	15	28	12
R4	9	30	20

Требуется выбрать лучший проект легкового автомобиля для производства, используя критерий Вальда, Сэвиджа, Гурвица при коэффициенте пессимизма 0,1. Сравнить решения и сделать выводы.