|
|
Лабораторная работа №1 Решение логических задач. Лабораторная работа 1 Решение логических задач Цель работы
Лабораторная работа №1
Решение логических задач
Цель работы: ознакомиться с основными функциями алгебры логики, освоить навыки решения логических задач.
Краткие теоретические сведения
Для решения логических задач применяется алгебра логики или булева алгебра.
В ее основу положено элементарное логическое высказывание. Таким высказыванием называется высказывание, которое может быть только истинным или ложным.
Для упрощения действий элементарные высказывания обозначаются буквами, а истину и ложь логическими единицами и нулем соответственно. Тогда простые элементарные высказывания можно связать между собой с помощью логических функций и, зная, как они работают, рассчитывать их.
Основные функции (логические операции) алгебры логики следующие:
Конъюнкция (логическое умножение): в естественном языке соответствует союзу и, обозначается &.
Конъюнкция – это логическая операция, ставящая в соответствие каждым двум простым высказываниям составное высказывание, являющееся истинным тогда и только тогда, когда оба исходные высказывания истинны.
Дизъюнкция - (логическое сложение): в естественном языке соответствует союзу или, обозначается V.
Дизъюнкция – это логическая операция, которая каждым двум простым высказываниям ставить в соответствие составное высказывание, являющееся ложным, и истинным, когда хотя бы одно из двух образующих его высказываний истинно.
Инверсия – (отрицание): в естественном языке соответствует словам «неверно, что…» и частице не, обозначается Ā.
Инверсия – это логическая операция, которая каждому простому высказыванию ставит в соответствие составное высказывание, заключающееся в том, что исходное высказывание отрицается.
Контрольный пример
Задача 1. «Пять офицеров»
В одной из горячих точек служили 5 офицеров: генерал, полковник, майор, капитан и лейтенант. Один из низ сапер, другой – пехотинец, третий – танкист, четвертый – связист, пятый – артиллерист. У каждого из них есть сестра. И каждый из них женат на сестре своего однополчанина. Вот что еще известно об этих офицерах:
По меньшей мере, один из родственников связиста старше его по званию.
Капитан никогда не служил в Хабаровске.
Оба родственника-пехотинца и оба родственника-танкиста служили раньше в Мурманске. Ни один родственник генерала в Мурманске не был.
Танкист служил в Твери вместе с обоими своими родственниками, а лейтенант там не служил.
Полковник служил в Махачкале вместе со своими родственниками.
Танкист не служил в Махачкале. Там служил только один из его родственников.
Генерал служил с обоими своими родственниками в Хабаровске, а в Махачкале он не бывал.
Артиллерист не служил ни в Хабаровске, ни в Твери.
Определите, кто из офицеров какое звание имеет?
Решение задачи:
Ясно, что каждый офицер имеет двух родственников. Один из них - брат жены, а другой - муж сестры. Обозначим для удобства каждого офицера буквой и расположим их так, чтобы соседом каждого были его родственники (рис. 1.1.).
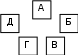
Рис. 1.1. Расположение по порядку
Пусть пехотинец будет обозначен буквой А. Поскольку трое из офицеров служили в Мурманске, а двое там не были, то танкисту должна соответствовать либо буква В, либо Г. Допустим, что танкист - В. Отсюда следует (с учетом условия задачи), что А и В не служили в Мурманске и что Б - генерал. Продолжая рассуждать, приходим к выводу, что Б, В и Г служили в Твери. Поэтому лейтенантом должен быть А или Д и букве Д должен соответствовать артиллерист. Далее, либо В и Г, либо В и Б не служили в Свердловске. Следовательно, А, Д и Б либо А, Д и Г служили в Свердловске. А поскольку мы знаем, что Б не служил в Свердловске, это значит, что там служили А, Д и Г и что Д - полковник. Таким образом, А - лейтенант.
Переходим к следующему этапу решения. A, Б и В служили в Хабаровске, а Д там не служил. Нам известно, что капитан в Хабаровске не служил. Поскольку капитал не может быть Д, следовательно, ему соответствует буква Г. Далее приходим к заключению, что В - майор. Известно, что по меньшей мере один офицер должен быть старше по званию, чем связист. Следовательно, связист не может быть Б и должен быть Г, а саперу соответствует буква Б.
Таким образом, в итоге получается, что лейтенант - пехотинец, генерал - сапер, майор - танкист, капитан - связист, полковник - артиллерист.
Задача 2. «Финальный забег»
Каждый второй пассажир в автобусе в увлечением читал спортивный раздел газеты, а остальные оживленно обсуждали последние спортивные новости. Иван Михайлович не успел купить газету, и ему не оставалось ничего другого, как заглядывать в газеты, развернутые другими пассажирами, и ловить доносившиеся до него обрывки разговоров.
Главной новостью дня был состоявшийся накануне финал эстафеты 4х100 м. для мужчин. В финал после упорной борьбы вышли команды шести стран: европейские команды А и B, африканские команды C и D, и 2 команды-представительницы американского континента E и F.
Иван Михайлович охотно узнал бы, как распределились места среди участников финала, но сделать это оказалось непросто. В тот день Иван Михайловичу особенно не везло: стоило ему пристроится к кому-нибудь, чтобы заглянуть через плечо, как счастливый обладатель спортивной газеты тотчас переворачивал страницу, а доносившиеся со всех сторон реплики знатоков и ценителей спроса были маловразумительными.
Выйдя из автобуса, Иван Михайлович смог восстановить в памяти лишь следующие крохи информации.
Команда А одержала победу над командой В.
Африканская команда получила золотые медали.
Команда В одержала победу над командой D.
По всему было видно, что первое и второе места достанутся американским командам, и вдруг в последний момент между ними вклинилась европейская команда.
Африканская команда отстала от всех остальных участников финала.
Первыми финишировали 3 африканских бегуна.
Команда F одержала победу над командой В.
Команда Е одержала победу над командой F.
В составе европейских команд не было африканских спортсменов.
Располагая этими отрывочными сведениями, Иван Михайлович попытался восстановить, как распределились места между шестью командами, участвовавшими в финале эстафетного бега, но тщетно.
Наконец, после тщательного анализа Иван Михайлович понял, что одна из девяти перечисленных выше посылок ложная. Он что-либо не так понял, либо плохо разглядел, либо неправильно вспомнил.
Все остальные посылки истинны.
Как распределились места между шестью командами, принимавшими участие в финальном забеге?
Решение задачи:
Для того чтобы решить задачу, необходимо, прежде всего, выяснить, какое из девяти приведенных утверждений ложно.
Итак, проанализируем данные утверждения. Если утверждение (9) заведомо верно (по условию задачи), то нетрудно установить, что утверждения (4), (5), и (6) не могут быть истинными одновременно.
Действительно, если истинно утверждение (6), то 3 первые места разделили между собой 2 африканские и 1 американская команды, либо 1 африканская и 2 американские команды. Но по утверждению (5) 2 африканские команды не могли быть среди тех, кто вышел на первые три места, а по утверждению (4) 2 американские команды могли занять лишь первое и третье места. Кроме того, из этого же утверждения (4) следует, что на второе место вышла европейская команда и, следовательно, среди обладателей трех первых мест не было ни одной африканской команды.
Таким образом, ложные сведения должны содержаться в каком-то из утверждений (4), (5) и (6), а остальные утверждения истинны, т. к. по условию задачи ложным является только одно утверждение. Воспользуемся сначала заведомо истинными утверждениями.
Объединим утверждения (1), (3) и (7) в одно, т. к. они взаимосвязаны между собой. Прочитав их в последовательности (1)-(7)-(3), приходим к следующему выводу: если исключить команды С и Е, то представители остальных команд могли прийти к финишу лишь в последовательности A, F, В, D. Следовательно, среди команд, занявших 3 первые места, заведомо должна быть европейская команда А. В худшем случае, она могла выйти на третье место, но оказалась среди призеров. Это означает, что утверждение (6) ложно. Чтобы определить, какое место заняла каждая из шести команд, расположим истинные утверждения в следующем порядке: (2), (4). (5), (8), (1)- (7)-(3), (9).
Как видно из утверждений (2) и (1)-(7)-(3), первое место могла занять лишь команда С, поскольку команда D заведомо не вышла на первое место. По утверждению (5), команда D могла занять лишь последнее, шестое место.
Утверждения (8) и (1)-(7)-(3) позволяют схематически изобразить распределение мест между четырьмя остальными командами так, как показано на рис. 1.2 (острие стрелки направлено к команде, показавшей лучшее время, конец - к команде, занявшей последнее место).
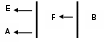
|
|
|
 Скачать 454.13 Kb.
Скачать 454.13 Kb.