Лабораторная работа 1 Решить задачу линейного программирования графическим способом
 Скачать 223.12 Kb. Скачать 223.12 Kb.
|
|
ФГБОУ ВО Уфимский Государственный Авиационный Технический Университет Кафедра АСУ Отчет по лабораторной работе №1 по дисциплине «Методы оптимизации» Вариант: 2 Выполнила: ст. гр. ПИ-312з Хасимов А. Проверила: Кондратьева О. Уфа 2021 Лабораторная работа №1 Решить задачу линейного программирования графическим способом При откорме каждое животное должно получать не менее 10 ед. белков, 8 ед. углеводов и 11 ед. протеина. Для составления рациона используют два вида корма, представленных в следующей таблице:
Стоимость 1 кг корма первого вида – 4 д.е., второго – 7 д.е. Составьте дневной рацион питательности, имеющий минимальную стоимость. Ход работы: Идентифицируем переменные задачи: Обозначим х1 – количество корма 1 вида и х2 – количество корма 2 вида. Животные должны получать необходимый минимум полезных веществ. Также, их количество не должно быть отрицательным. Запишем ограничения по ресурсам математически: 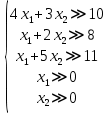 Цель задачи состоит в покупке корма за минимальную стоимость, поэтому целевая функция будет выглядеть: 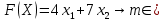 Получим пять уравнений прямых, заменив знак неравенства на равенство: 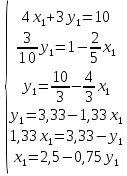 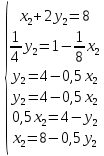 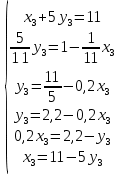 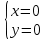 5. Построим эти прямые на координатной плоскости: 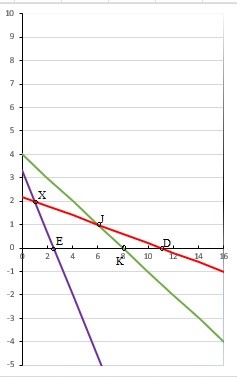 6. Найдем полуплоскости, определяемые каждым из ограничений задачи в соответствии со знаком неравенства: 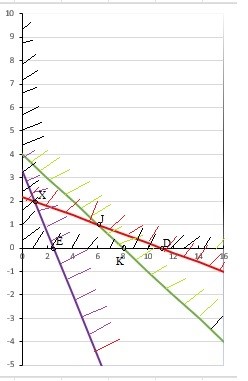 7. Найдем область допустимых решений, т.е. многоугольник решений и заштрихуем его. 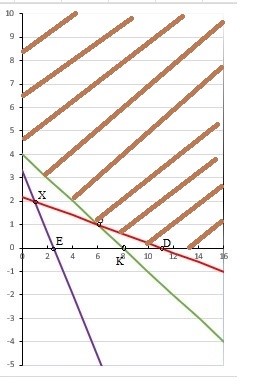 8. Построим направляющий вектор  по двум точкам – (0;0) и (4;7) и найдем точку оптимума, для этого построим прямую по двум точкам – (0;0) и (4;7) и найдем точку оптимума, для этого построим прямую  через начало координат и перпендикулярно вектору через начало координат и перпендикулярно вектору  , будем передвигать эту прямую параллельно самой себе в направлениях вектора , будем передвигать эту прямую параллельно самой себе в направлениях вектора 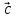 (вверх и вправо) до тех пор, пока прямая не коснется крайней точки многоугольника решений, то есть точки A. (вверх и вправо) до тех пор, пока прямая не коснется крайней точки многоугольника решений, то есть точки A.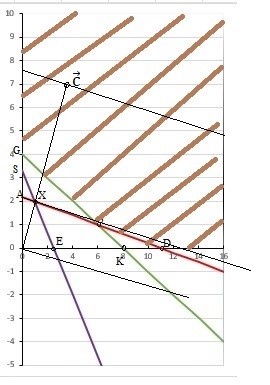 9. Найдем координаты точки A. Решим систему уравнений: 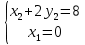 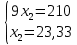 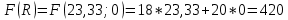 Ответ: предприятию необходимо производить 23,33 ед. продукции вида П1 и 0 ед. продукции вида П2, при этом прибыль от реализации будет максимальной и равна 420 ден.ед. | |||||||||||||||||
