СТРУКТУРНЫЙ И КИНЕМАТИЧЕСКИЙ АНАЛИЗ ПЛОСКОГО МЕХАНИЗМА. лаб 1. Лабораторная работа 1 структурный и кинематический анализ плоского механизма выполнил студент
 Скачать 392.08 Kb. Скачать 392.08 Kb.
|
|
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ БАЛТИЙСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ «ВОЕНМЕХ» им. Д.Ф. УСТИНОВА Кафедра системы приводов, мехатроника и робототехника (И8) Дисциплина «Теория машин и механизмов» Лабораторная работа № 1 СТРУКТУРНЫЙ И КИНЕМАТИЧЕСКИЙ АНАЛИЗ ПЛОСКОГО МЕХАНИЗМА
Санкт-Петербург 2022 г. СТРУКТУРНЫЙ АНАЛИЗ МЕХАНИЗМА На рисунке представлена схема исследуемого четырёхзвенный рычажного механизма с тремя подвижными звеньями. 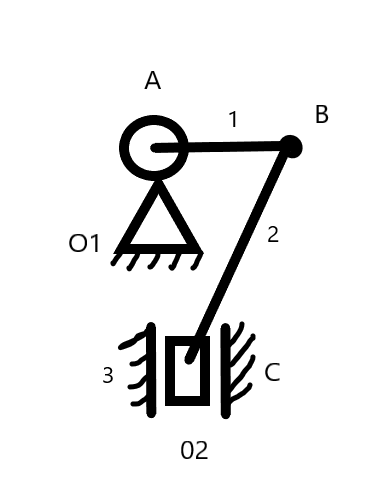 Число степеней свободы по формуле Чебышева для плоских механизмов W=3n-2p5-p4=3*3-2*4=1. где n – количество подвижных звеньев, p5 и p4 –количество кинематических пар 5-го и 4-го класса соответственно. 2. КИНЕМАТИЧЕСКИЙ АНАЛИЗ МЕХАНИЗМА Кинематический анализ производится экспериментально-аналитически. Функцию S(ϕ1) положения ползуна 3 в зависимости от угла поворота кривошипа 1 получаем экспериментально в виде таблицы с шагом 10о по углу поворота кривошипа. Результаты эксперимента представлены в таблице 1.1. Таблица 1.1
Полагая, что кривошип вращается с постоянной угловой скоростью ω1=29c-1 , следовательно, ϕ1=ω1t, получим функцию положения от времени S(t). Для этого вычислим шаг таблицы по времени: Δt = Δϕ1 рад /ω1 = 0,17453/29 = 0,006018 с, где Δϕ1 рад = Δϕ1°/180 = 10/180 = 0,17453 рад. Для аналитической обработки функции S(t) проведем ее аппроксимацию и фильтрацию пятью методами. Обработку данных эксперимента проведем с помощью программы ApproxFSP.exe.6.0. 3. Аппроксимация функции положения тригонометрическим рядом Фурье. В этом случае функцию S(t) разлагаем в тригонометрический ряд Фурье и дифференцированием ряда определяем зависимости скорости v(t) и ускорения а(t) ползуна. При этом необходимо решить вопрос об оптимальном числе членов ряда. Разложение функции в такой ряд означает её приближенную замену тригонометрическим полиномом, являющимся суммой ряда: Sф(t)= 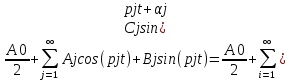 ) )где Aj , Bj – коэффициенты ряда, pj = 2πj/T – частоты, по которым производится разложение, T = 2π/ω1=2π/28 = 0.224 с – время полного оборота кривошипа Cj– амплитуда j-й гармоники, j – её фаза, m – число членов ряда. В данном случае функция S(t) задана таблицей значений в конечном числе точек n = 36, поэтому максимальное число членов ряда mmax = n/2 = 36/2 = 18. На первом этапе разложим S(t) в ряд с максимально возможным числом членов m = 18. Результаты представлены на рис.1 и в табл.1. В этом случае значения ряда Фурье в узлах практически совпадают с данными эксперимента. 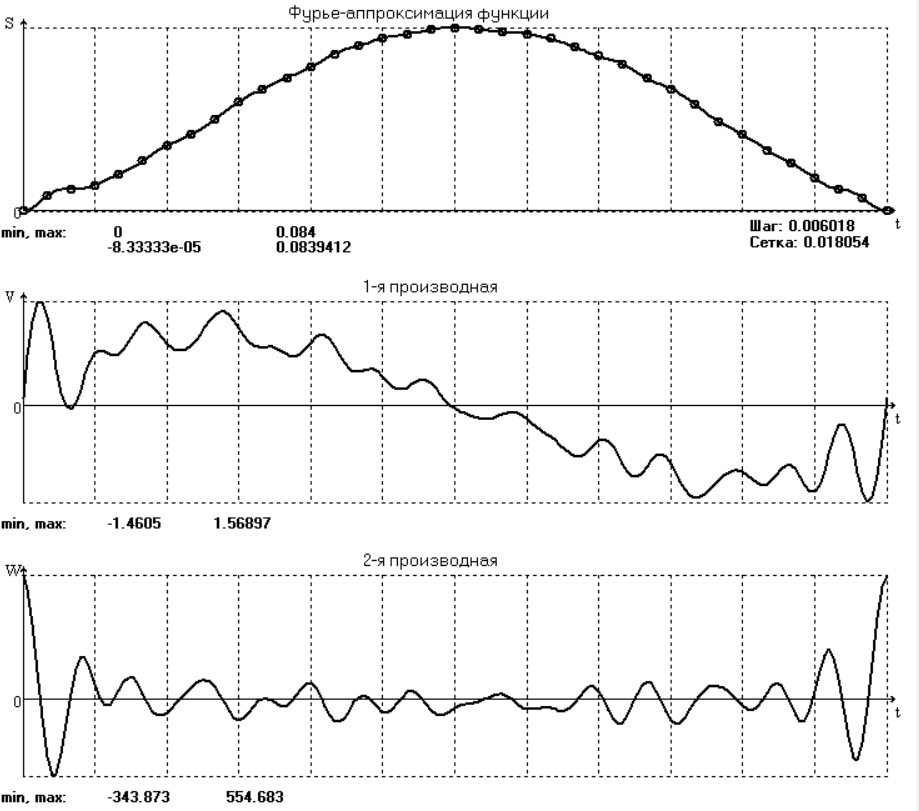 На графике скорости и особенно ускорения явно видны паразитные осцилляции, вызванные погрешностями работы механизма и погрешностями замера значений S(t). Во многих случаях возникает потребность сглаживания такого рода зависимостей.  Оценим значимость членов ряда с помощью амплитудного спектра, показанного на рис.2 и в табл.2. 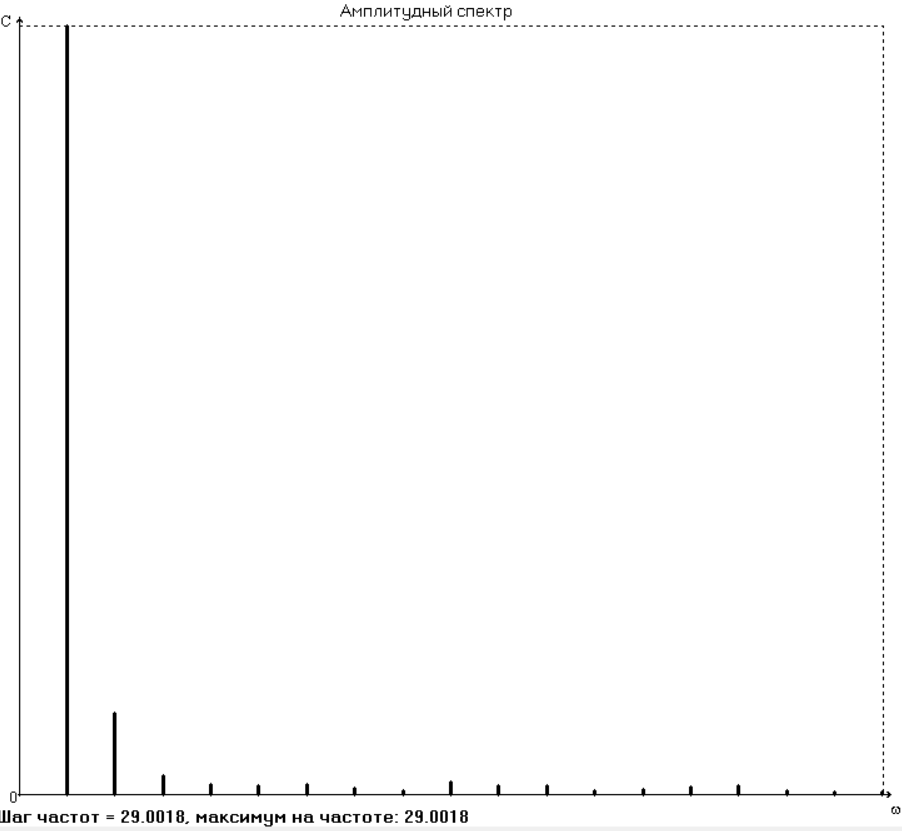  Анализ амплитудного спектра исследуемой функции показывает, что существенными, кроме А0/2, являются слагаемые ряда, соответствующие всем частотам, кроме 3-й, поэтому проведём разложение в ряд и аппроксимацию функции с улётом первых двух частот. Результаты представлены на рис. 3 и в табл. 3. Очевидно, что получена сглаживающая аппроксимация. При этом аппроксимирующее выражение для данной функции с учетом только первых трех членов ряда приобретает вид: Sф(t)=0,04847+0,03861*sin(29t + 1,4964) +0,004093*sin(58t+1,5096). 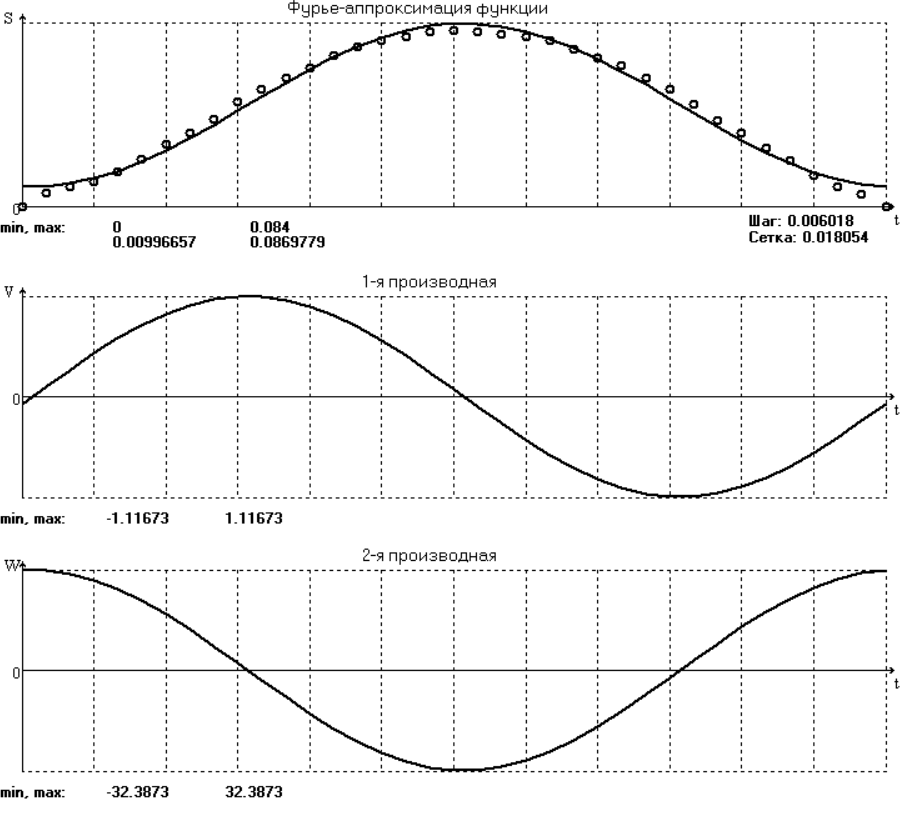  Вывод: С помощью структурного анализа механизма мы определили количество звеньев, количество и типы кинематических пар, наличие пассивных звеньев, вычислили число степеней свободы. Мы определили кинематические параметры движения (перемещение, скорость, ускорение), связанные друг с другом как первообразные и производные функции. Функции скорости и ускорения мы получили с помощью математической обработки (с помощью аппроксимации функции положения тригонометрическим рядом Фурье). Ряд Фурье позволяет производить сглаживающую аппроксимацию. Для сглаживающей аппроксимации следует при разложении учитывать лишь первые основные частоты, что определяется по амплитудному спектру. Тригонометрические ряды Фурье хорошо аппроксимируют гладкие периодические функции. Литература 1. Лавров В.Ю. Введение в теорию механизмов и машин (ТММ): учебное пособие / Балт. гос. техн. ун-т. СПб., 2016. 151 с. 2. Лавров В.Ю. Курсовое проектирование по теории машин и механизмов в среде программы Mechanic: учебное пособие / Балт. гос. техн. ун-т. СПб., 2013. 32 с. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
