хз. методические указания к лабораторным_07 2. Лабораторная работа 1. Технология работы с формулами на примере подсчета количества разных оценок в группе в экзаменационной ведомости
 Скачать 245.5 Kb. Скачать 245.5 Kb.
|
|
Лабораторная работа №1. Технология работы с формулами на примере подсчета количества разных оценок в группе в экзаменационной ведомости. Задание. Сформируйте структуру таблицы (рис. 1) и заполните ее постоянными значениями (подпись экзаменатора ставить не надо). ЭКЗАМЕНАЦИОННАЯ ВЕДОМОСТЬ Группа__________ Дисциплина_________________
«отлично» ____________________________________ «хорошо» _____________________________________ «удовлетворительно»____________________________ «неудовлетворительно»__________________________ «неявки»_______________________________________ ИТОГО ________________________________________ Рис.1. Форма экзаменационной ведомости В созданной рабочей книге с экзаменационной ведомостью рассчитайте: количество оценок (отлично, хорошо, удовлетворительно, неудовлетворительно, неявок), полученных в данной группе; общее количество полученных оценок. Технология выполнения. Введите в cоответствующие ячейки тексты заголовка и шапки таблицы в соответствии с рисунком. Отформатируйте ячейки А1:Е1 и A3:E3: выделите блок ячеек, нажмите правую кнопку мыши для вызова контекстного меню; введите команду контекстного меню Формат ячеек; на вкладке выравнивание выберите опции: По горизонтали: по центру выделения. По вертикали: по верхнему краю нажав кнопку <Размер>, выберите размер шрифта, например 14 пт; при необходимости выделите текст жирным шрифтом, нажав на панели инструментов кнопку <Ж>. Cформируйте шапку таблицы, задав параметры выравнивания вводимого текста: выделите блок ячеек А5:J5, где располагается шапка таблицы; вызовите контекстное меню и выберите команду ; на вкладке Выравнивание задайте параметры: По горизонтали: по значению. По вертикали: по верхнему краю. Переносить по словам: поставить флажок. Ориентация: горизонтальный текст (по умолчанию). нажмите кнопку Установите ширину столбцов таблицы в соответствии с рисунком. Для этого: подведите указатель мыши к правой черте клетки с именем столбца, например В, так, чтобы указатель изменил свое изображение; нажмите левую кнопку мыши и, удерживая ее, протащите мышь так, чтобы добиться нужной ширины столбца или строки. аналогичные действия проделайте с остальными столбцами. Заполните ячейки столбца В данными о студентах учебной группы, приблизительно 10 — 15 строк (фамилии и оценки). Отформатируйте данные. Присвойте каждому студенту порядковый номер: введите в ячейку А6 число 1; установите курсор в нижний правый угол ячейки А6 так, чтобы указатель мыши приобрел изображение креста и, нажав правую кнопку мыши, протяните курсор на требуемый размер; выполните команду локального меню Заполнить. После списка студентов в нижней части таблицы согласно рисунку введите в ячейки столбца А текст итоговых строк: Отлично, Хорошо, Удовлетворительно, Неудовлетворительно, Неявка, ИТОГО. Объедините две соседние ячейки для более удобного представления текста итоговых строк. Технологию объединения покажем на примере объединения двух ячеек столбцов А и В, в которых будет расположена надпись Отлично: выделите две ячейки; вызовите контекстное меню и выберите команду Формат ячеек; на вкладке Выравнивание установите флажок Объединение ячеек и нажмите кнопку <ОК>; аналогичные действия проделайте с остальными ячейками, где хранятся названия итоговых ячеек. Сохраните рабочую книгу, для которой файл будет иметь тип xls: выполните команду Файл, Сохранить как; в диалоговом окне установите следующие параметры: Папка: имя вашего каталога. Имя файла: Session1. Тип файла: Книга Microsoft Excel. Введите названия (5,4,3,2, неявки) соответственно в ячейки F5, G5, H5, I5, J5 вспомогательных столбцов. В эти столбцы F – J введите вспомогательные формулы. Суть формулы состоит в том, что вид оценки фиксируется напротив фамилии студента в ячейке соответствующего вспомогательного столбца как 1. Например, студент Снегирев получил оценку 5, тогда в ячейке F6 должна стоять 1, а в остальных вспомогательных столбцах G – J в данной строке – 0. Для ввода исходных формул воспользуйтесь Мастером функций. Рассмотрим эту технологию на примере ввода формулы в ячейку F6: установите курсор в ячейку F6 и выберите мышью на панели управления инструментов кнопку Мастера функций; в 1-м диалоговом окне выберите вид функции: Категория – логические. Имя функции – ЕСЛИ. щелкните по кнопке во 2-м диалоговом окне, устанавливая курсор в каждой строке, введите соответствующие операнды логической функции: Логическое выражение – D6=5. Значение, если истина, – 1. Значение, если ложно, – 0. щелкните по кнопке Примечание. Для ввода адреса ячейки в строку наберите его сами или щелкните в ячейке D6 правой кнопкой мыши. С помощью Мастера функции введите формулы аналогичным способом в остальные ячейки данной строки. Скопируйте эти формулы во все остальные ячейки дополнительных столбцов выделите блок ячеей F6 : J6; установите курсор в правый нижний угол выделенного блока и после появления черного крестика, нажав правую кнопку мыши, протащите ее до конца таблицы Экзаменационная ведомость; выберите в контекстном меню команду Заполнить значения Определите имена блоков ячеек по каждому дополнительному столбцу. Рассмотрим это на примере дополнительного столбца F: выделите все значения дополнительного столбца, например F6: <адрес ячейки в столбце, в которой находится последнее значение>; введите команду Вставка, Имя, Присвоить; в диалоговом окне в строке Имя введите слово ОТЛИЧНО: щелкните по кнопке <Добавить>; проведите аналогичные действия с остальными столбцами и задайте имена блоков ячеек: ХОРОШО, УДОВЛЕТВОР, НЕУД, НЕЯВКА. Выделите столбцы F - J целиком и сделайте их скрытыми: установите курсор на названии столбцов и выделите столбцы F –J; введите команду Формат, Столбец, Скрыть. Введите формулу подсчета суммарного количества полученных оценок определенного вида, используя имена блоков ячеек с помощью Мастера функций. Покажем это на примере подсчета количества отличных оценок: установите указатель мыши в ячейку С13 подсчета количества отличных оценок; щелкните по кнопке Мастер функций; в диалоговом окне Мастер функций выберите: Категория — Математические, функция — СУММ; щелкните по кнопке <ОК>; в следующем диалоговом окне в строке Число 1 установите курсор и введите команду Вставка, Имя, Вставить; в появившемся диалоговом окне выделите имя блока ячеек Отлично, щелкните по кнопке <ОК>; повторите аналогичные действия для подсчета количества других оценок в ячейкахС14-С17. Подсчитайте общее количество (ИТОГО) всех полученных оценок другим способом: установите курсор в пустой ячейке С18 (рядом с ИТОГО). Эта ячейка должна обязательно находиться под ячейками, где подсчитывались суммы по всем видам оценок; щелкните по кнопке <> ; выделите блок ячеек, где подсчитывались суммы по всем видам оценок, и нажмите клавишу <Enter>. Переименуйте текущий лист: установите курсор на имени текущего листа, и вызовите контекстное меню; выберите параметр Переименовать и введите новое имя, например Экзамен 1. Скопируйте несколько раз текущий лист Экзамен 1: установите курсор на имени текущего листа и вызовите контекстное меню; выберите параметр Переместить/Скопировать, поставьте флажок Создавать копию и параметр Переместить в конец, нажмите <ОК>. Сохраните рабочую книгу с экзаменационными ведомостями (она понадобится для следующего задания). Лабораторная работа №2 Задание. Подготовьте для группы ведомость (рис.2) назначения студентов на стипендию по результатам экзаменационной сессии. ВЕДОМОСТЬ НАЗНАЧЕНИЯ НА СТИПЕНДИЮ Группа №_______ Минимальный размер стипендии _____________
Итого стипендиальный фонд по группе – __________________ Рис. 2. Форма стипендиальной ведомости Последовательность действий: Загрузите экзаменационную ведомость с оценками по трем предметам (информатика, мат. анализ, культурология ) из предыдущего задания. На новом листе создайте ведомость стипендии (см. рис. 2) и скопируйте в нее список группы с порядковыми номерами и номерами зачетных книжек из экзаменационной ведомости предыдущего задания. Вычислите средний балл по результатам сдачи экзаменов по каждому студенту. Используя минимальное значение стипендии, и учитывая, что сданы все экзамены, введите формулу начисления стипендии по условию: если средний балл не менее 4,5, выплачивается 50%-ная надбавка к минимальной стипендии; если средний балл от 3 (включительно) до 4,5, выплачивается минимальная стипендия; если средний балл меньше 3, стипендия не выплачивается. Обратите внимание, что наличие неявки или двойки за экзамен говорит о том, что экзамен не сдан, и, следовательно, стипендия не начисляется. Подсчитайте сумму стипендиального фонда для всей группы. Технология выполнения Загрузите рабочую книгу с экзаменационными ведомостями. Создайте в этой книге новый лист — Стипендия, на который из столбцов А и В листа Экзамен 1 скопируйте фамилии и порядковые номера студентов. Оформите название и шапку ведомости назначения на стипендию согласно рис.2.(задайте шрифт и тип выделения — полужирный). Укажите размер минимальной стипендии в ячейке D3; Вставьте два дополнительных столбца перед столбцом Стипендия и введите их названия — Средний балл и Кол-во сданных экзаменов. Введите формулу вычисления среднего балла студента в ячейку С6 для первого студента, например Снегирева. Для этого: установите курсор в ячейке С6; щелкните по кнопке <Мастер функций> на панели Стандартная и выберите в диалоговом окне параметры: Категория: Статистические; Имя: СРЗНАЧ. щелкните по кнопке <ОК>, появится панель ввода аргументов функции СРЗНАЧ; установите курсор в 1-й строке (имя Число 1) панели ввода аргументов функции, щелкните на названии листа Экзамен 1 и выберите ячейку D6 с оценкой конкретного студента по первому экзамену; аналогичным образом в качестве параметров Число2 и Число 3 выберите ячейку D6 с оценкой того же студента по второму экзамену и ячейку D6 с оценкой по третьему экзамену; щелкните по кнопке <ОК>; в ячейке С6 появится значение, рассчитанное по формуле СРЗНАЧ('Экзамен 1`!D6;'Экзамен 1 (2)'D6;'Экзамен 1 (3)'D6). Скопируйте формулу по всем ячейкам столбца С. Введите в столбец D формулу подсчета количества сданных каждым студентом экзаменов с учетом неявок и двоек, при этом технология ввода будет аналогична описанной в п.6, отличие заключается в использовании функции СЧЁТЕСЛИ. Окончательная формула в ячейке имеет вид: =СЧЁТЕСЛИ('Экзамен 1'!D6;">2")+СЧЁТЕСЛИ('Экзамен 1 (2)'!D6;">2")+СЧЁТЕСЛИ('Экзамен 1 (3)'!D6;">2"). Скопируйте формулу по всем ячейкам столбца D. Введите формулу для вычисления размера стипендии студента в ячейку Е6. Эта формула может иметь следующий вид: =ЕСЛИ(И(С6>=4,5;D6=3);$D$3*1,5;ЕСЛИ(И(С6>=3;D6=3);$D$3;0)) Технология ввода формулы аналогична описанной в п.6. Для ввода вложенных функций можно пользоваться кнопкой вызова функций. Скопируйте эту формулу в другие ячейки столбца Е так же, как вы делали в п. 7 и 9. Проверьте работоспособность таблицы: вводите другие оценки в экзаменационные ведомости; измените минимальный размер стипендии. Подсчитайте сумму стипендиального фонда для всей группы. Лабораторная работа №3. Графическое решение систем уравнений Задание. Решить графически систему уравнений: Технология выполнения. Системы уравнений с двумя неизвестными могут быть приближенно решены графически. Их решением являются координаты точки пересечения линий, соответствующих уравнениям систем. При этом точность решения будет определяться величиной шага дискретизации (чем шаг меньше, тем точность выше). Рассмотрим пример графического решения системы двух уравнений. Пример. Пусть необходимо найти решения системы Решение. Для построения диаграмм прежде всего необходимо ввести данные в рабочую таблицу. Вводим в ячейку А1 слово Аргумент. Затем в ячейку А2 – первое значение аргумента – 0. Далее будем вводить приращения аргумента с шагом 0,2. Введем в ячейку А3 сумму левой границы диапазона плюс шаг (0,2). Затем, выделив блок ячеек А2:А3, автозаполнением получаем все значения аргумента (за правый нижний угол блока протягиваем до ячейки А17). Далее требуется ввести значения функции (в примере синуса). В ячейку В1 вводим слово Синус и устанавливаем табличный курсор в ячейку В2. Здесь должно оказаться значение синуса, соответствующе6е значению аргумента в ячейке А2. Для получения значения синуса воспользуемся специальной функцией: нажмем на панели инструментов кнопку Вставка функций (fx). В появившемся диалоговом окне Мастер функций-шаг 1 из 2 слева в поле Категория указаны виды функций. Выбираем Математические. Справа в поле Функция выбираем функцию SIN. Нажимаем кнопку ОК. Появляется диалоговое окно SIN. Наведя указатель мыши на серое поле окна, при нажатой левой кнопке сдвигаем его вправо, чтобы открыть столбец данных (А). Указываем значение аргумента синуса щелчком мыши на ячейке А2 (рис. ). Нажимаем кнопку ОК. В ячейке В2 появляется 0. Теперь необходимо скопировать функцию из ячейки В2 в ячейки В3:В17. Осуществляем это автозаполнением (за правый нижний угол ячейки В2 протягиваем до ячейки В17). Значения синуса получены.
Рис.3. Пример заполнения таблицы значений SIN Аналогично получаем значения косинуса. В ячейку С1 вводим имя функции — Косинус. Устанавливаем табличный курсор в ячейку С2. Для получения значения косинуса нажимаем на панели инструментов кнопку Вставка функции (fx). В появившемся диалоговом окне Мастер функций-шаг 1 из 2 слева в поле Категория выбираем Математические. Справа в поле Функция выбираем функцию COS. Нажимаем кнопку ОК. Появляется диалоговое окно COS. Наведя указатель мыши на серое поле окна, при нажатой левой кнопке сдвигаем его вправо, чтобы открыть столбец аргумента (А). Указываем значение аргумента косинуса щелчком мыши на ячейке А2. Нажимаем кнопку ОК. В ячейке С2 появляется 1. Автозаполнением копируем формулу (за правый нижний угол ячейки С2 протягиваем до ячейки С17). Значения косинуса получены. Далее по введенным в рабочую таблицу данным необходимо построить диаграмму. Щелчком указателя мыши по кнопке на панели инструментов вызываем Мастер диаграмм. В появившемся диалоговом окне выбираем тип диаграммы График, вид — левый верхний. После нажатия кнопки Далее с помощью мыши указываем диапазон данных — В1:С17. Проверяем положение переключателя Ряды : в столбцах. Выбираем вкладку Ряд и с помощью мыши вводим диапазон подписей оси x: А2:А 17. Нажав кнопку Далее, вводим название диаграммы — Система, название осей х и у Аргумент и Значения, соответственно. Нажимаем кнопку Готово. 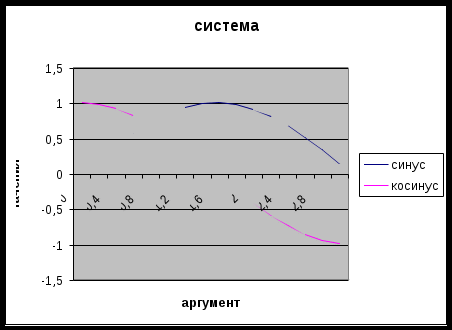 Рис.4. Диаграмма к примеру Получена диаграмма кривых синуса и косинуса (рис. 4). Как видно из диаграммы, система имеет решение (есть точка пересечения), и оно единственное (в заданном диапазоне имеется только одна точка пересечения). Таким образом, решением системы в заданном диапазоне являются координаты точки пересечения кривых. Для их нахождения необходимо навести указатель мыши на точку пересечения и щелкнуть левой кнопкой. Появляется надпись с указанием искомых координат: Ряд «Косинус». Точка «0,8». Значение: 0,69670671. Здесь Точка «0,8» соответствует x, а Значение: 0,69670671 —y. Таким образом, приближенное решение системы х= 0,8; у = 0,697. Лабораторная работа №4. Поверхности в трёхмерном пространстве. Задание. 1. Построить верхнюю часть эллипсоида: Диапазоны изменения переменных x и y: 2. Построить верхнюю часть однополостного гиперболоида: Диапазоны изменения переменных x и y: 3. Построить гиперболический параболоид: Диапазоны изменения переменных: 4. Построить верхнюю часть конуса Диапазоны изменения переменных x и y: Технология выполнения Для построения любой из этих фигур в Excel каноническое уравнение необходимо разрешить относительно переменной z (представить в виде Пример. Рассмотрим построение эллипсоида в Excel на примере уравнения Пусть необходимо построить верхнюю часть эллипсоида, лежащую в диапазонах: х Решение. Вначале необходимо разрешить уравнение относительно переменнойz. В примере Введем значения переменной х в столбец А. Для этого в ячейку А1 вводим символ x В ячейку А2 вводится первое значение аргумента — левая граница диапазона (–3) В ячейку A3 вводится второе значение аргумента — левая граница диапазона плюс шаг построения (-2,5). Затем, выделив блок ячеек А2:АЗ, автозаполнением получаем все значения аргумента (за правый нижний угол блока протягиваем до ячейки А14). Значения переменной у вводим в строку 1. Для этого в ячейку В1 вводится первое значение переменной — левая граница диапазона (–2). В ячейку С1 вводится второе значение переменной — левая граница диапазона плюс шаг построения (–1,5). Затем, выделив блок ячеек В1:С1, автозаполнением получаем все значения аргумента (за правый нижний угол блока протягиваем до ячейки J1). Далее вводим значения переменной z. Для этого табличный курсор необходимо поместить в ячейку В2 и на панели инструментов Стандартная нажать кнопку Вставка функции (fx). В появившемся диалоговом окне Мастер функций-шаг 1 из 2 слева поле Категория выбираем Математические. Справа в поле Функция выбираем функцию Корень. Нажимаем кнопку ОК. Появляется диалоговое окно Корень. В рабочее поле вводим подкоренное выражение: 1-$А2^2/9-В$1^2/4. Обращаем внимание что символы $ предназначены для фиксации адреса столбца А — переменной х и строки 1 — переменной у. Нажимаем кнопку ОК. В ячейке В2 появляется #ЧИСЛО! (при х= –3 и у= –2 точек рассматриваемого эллипсоида не существует). Теперь необходимо скопировать функцию из ячейки В2. Для этого автозаполнением (протягиванием вправо) копируем эту формулу вначале в диапазон B2:J2, после (протягиванием вниз) — в диапазон ВЗ:J4. В результате должна быть получена следующая таблица (рис.5).
Рисунок 5. Результаты вычислений точек эллипсоида из примера Для построения диаграммы на панели инструментов Стандартная необходимо жать кнопку Мастер диаграмм. В появившемся диалоговом окне Мастер диаграмм (шаг 1 из 4): тип диаграммы указываем тип диаграммы — Поверхность, и вид — Проволочная (прозрачная) поверхность (правую верхнюю диаграмму в правом окне). После чего нажимаем кнопку Далее в диалоговом окне. В появившемся диалоговом окне Мастер диаграмм (шаг 2 из 4): источник данных диаграммы необходимо выбрать вкладку Диапазон данных и в поле Диапазон мышью указать интервал данных B2:J14. Далее необходимо указать, в строках или столбцах расположены ряды данных. Это определит ориентацию осей х и у. В примере переключатель Ряды в с помощью указателя мыши установим в положение столбцах. Выбираем вкладку Ряд и в поле Подписи оси X указываем диапазон подписей, этого щелкните в нем указателем мыши и введите диапазон подписей оси А2:А14. Вводим значения подписей оси y. Для этого в рабочем поле Ряд указываем первую запись Ряд 1 и в рабочее поле Имя, активизировав его указателем мыши, вводим первое значение переменной у: –2. Затем в поле Ряд указываем вторую запись Ряд 2 и в рабочее поле Имя вводим второе значение переменной у: –1,5. Повторяем таким образом до последней записи — Ряд 9. После появления требуемых записей необходимо нажать кнопку Далее. В третьем окне требуется ввести заголовок диаграммы и названия осей. Для этого необходимо выбрать вкладку Заголовки, щелкнув на ней указателем мыши. Щелкнув в рабочем поле Название диаграммы указателем мыши, ввести с клавиатуры в поле название: Эллипсоид. Затем аналогичным образом ввести в рабочие поля Ось Х (категорий), Ось Y (рядов данных) и Ось Z (значений) соответствующие названия: x,y и z. Далее следует нажать кнопку Готово, и после небольшого редактирования будет получена следующая диаграмма (рис.6). 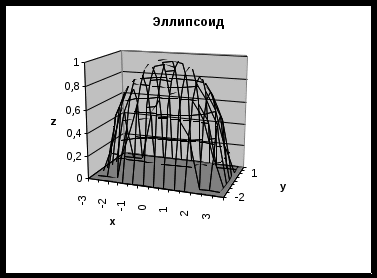 Рисунок 6. Лабораторная работа № 5. Решение систем линейных уравнений. Задание Решить систему линейных уравнений x1 – x2 + x3 = 3, 2x1 + x2 + x3 = 11, x1 + x2 +x3 = 8. Решение должно содержать подписи к данным («матрица», «вектор-столбец неизвестных», «определитель» и т.д.) Предварительно проверить, имеет ли эта система решение. Технология выполнения Система линейных уравнений в матричном виде записывается как Ax=b, (1), где А – матрица; x – вектор-столбец неизвестных; b – вектор-столбец свободных членов. Существует несколько способов решения системы (1), мы рассмотрим решение в общем виде (метод обратной матрицы). Будем считать, что квадратная матрица А является невырожденной, т.е. её определитель не равен нулю: det(A)0. В этом случае существует обратная матрица А-1. Тогда решение этой системы (1) x= А-1b. Т.о. для нахождения решения требуется найти обратную матрицу и умножить её слева на вектор b. Пример. Пусть необходимо решить систему линейных уравнений: Решение 1. Введите матрицу А (в данном случае размера 2 х 2) в диапазон А1:В2 Вектор В = (7 40) введите в диапазон С1:С2. 2. Найдите обратную матрицу А-1. Для этого: выделите блок ячеек под обратную матрицу. Например, выделите блок АЗ:В4 (указателем мыши при нажатой левой кнопке); нажмите на панели инструментов Стандартная кнопку Вставка функции; в появившемся диалоговом окне Мастер функций в рабочем поле Категория выберите Математические, а в рабочем поле Функция — имя функции МОБР. После этого щелкните на кнопке ОК; появившееся диалоговое окно МОБР мышью отодвиньте в сторону от исходной матрицы и введите диапазон исходной матрицы А1:В2 в рабочее поле Массив (указателем мыши при нажатой левой кнопке). Нажмите сочетание клавиш CTRL+SHIFT+ENTER; если обратная матрица не появилась в диапазоне АЗ:В4, то следует щелкнуть указателем мыши в Строке формул и повторить нажатие CTRL+SHIFT+ENTER. В результате в диапазоне АЗ:В4 появится обратная матрица: 3. Умножением обратной матрицы А-1 на вектор В найдите вектор X. Для этого: выделите блок ячеек под результирующий вектор X. Его размерность в данном примере 2 нажать на панели инструментов Стандартная кнопку Вставка функции; в появившемся диалоговом окне Мастер функций в рабочем поле Категория выберите Математические, а в рабочем поле Функция имя функции — МУМНОЖ. Щелкните на кнопке ОК; появившееся диалоговое окно МУМНОЖ мышью отодвиньте в сторону от исходных матриц и введите диапазон обратной матрицы A-1 — AЗ:В4 в рабочее поле Массив1 (указателем мыши при нажатой левой кнопке), а диапазон матрицы В–С1:С2– в рабочее поле Массив2. После этого нажмите сочетание клавиш CTRL+SHIFT+ENTER; если вектор X не появился в диапазоне СЗ:С4, то следует щелкнуть указателем мыши в строке формул и повторить нажатие CTRL+SHIFT+ENTER. В результате в диапазоне СЗ:С4 появится вектор X. Причем х=5 будет находиться в ячейке СЗ, а у = –4 — в ячейке С4. Можно осуществить проверку найденного решения. Для этого найденный вектор X необходимо подставить в исходное матричное уравнение A Проверка производится следующим образом. Выделить блок ячеек под результирующий вектор В. Его размерность в данном примере 2 Нажмите на панели инструментов Стандартная кнопку Вставка функции. В появившемся диалоговом окне Мастер функций в рабочем поле Категория выберите Математические, а в рабочем поле Функция – имя функции МУМНОЖ. Щелкните кнопкой ОК. Появившееся диалоговое окно МУМНОЖ мышью отодвиньте в сторону от исходных матриц и введите диапазон исходной матрицы А – А1:В2 в рабочее поле Массив1 (указателем мыши при нажатой левой кнопке), а диапазон матрицы Х – С3:С4 – в рабочее поле Массив2. После этого нажмите сочетание клавиш CTRL+SHIFT+ENTER. Если вектор В не появился в диапазоне D1:D2, то следует щелкнуть указателем мыши в строке формул и повторить нажатие CTRL+SHIFT+ENTER. В результате в диапазоне D1:D2 появится вектор В, и, если система решена правильно, появившийся вектор будет равен исходному b =(7 40). Т.к. не любая система линейных уравнений имеет решение, желательно до вычисления обратной матрицы найти определитель. Если det(A)0, система не вырожденная и решение существует. В противном случае дальнейшие действия смысла не имеют. Для нахождения определителя используйте функцию МОПРЕД из категории Математические. |
