ттт. Лабораторная работа. Лабораторная работа 1 Выявление погрешности измерений методом повторного замера более точным средством измерения фио

• Название: Лабораторная работа 1 Выявление погрешности измерений методом повторного замера более точным средством измерения фио
• Дата: 30.01.2022
• Размер: 37.78 Kb.
• Имя файла: Лабораторная работа.docx
• Тип: Лабораторная работа; #346835

Лабораторная работа №1 «Выявление погрешности измерений методом повторного замера более точным средством измерения»	ФИО
	Группа
	Дата
	Подпись

Цели работы:

1. Определить погрешность измерения определяющего размера у деталей контролируемой партии методом повторного измерения более точным измерительным прибором.

2. Проверить гипотезу о случайности и непреднамеренности отбора контролируемой выборки деталей
Результаты измерений

Таблица 1.1

№	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21	22	23	24	25
Размер детали, измеренный штангенциркулем а. мм	60,1	60,05	60,05	60,05	60	60,1	60,15	60,15	59,95	60,05	60,1	60,05	60,05	60,05	60,05	60,05	60,05	60,10	60,10	60,05	60,05	60,15	60,15	60,10	60,05
Размер детали, измеренный микрометром a* мм	60,05	60,04	60,05	60,02	60,07	60,14	60,10	60,01	60,08	60,11	60,06	60,04	60,06	60,04	60,06	60,07	60,04	60,08	60,06	60,04	60,06	60,14	60,12	60,07	60,07
Погрешность измерения ∆i = ai- ai*, мкм	50	10	0	30	-70	-40	50	140	-130	-60	40	10	-10	10	-10	-20	10	20	40	10	-10	10	30	30	-20

Обработка и анализ опытных данных

1.Выбор номинального размера и назначение квалитета точности изготовления анализируемой детали.

Номинальный размер: A = 60 мм

Для выбора квалитета проводится оценка параметров:

а) размах значений результатов измерений, полученных штангенциркулем (R,мкм):

R = a_max - a_min = 60,15 – 59,95 = 0,2 мм = 200 мкм

б) выборочное стандартное отклонение (S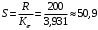, мкм):

мкм

По справочным данным для n = 25 значение, характеризующее поле рассеяния, составляет: 3,931

в) вероятное поле рассеяния отклонений размеров, принятое по нормальному закону распределения (𝜔, мкм):

𝜔 = 6∙S = 6∙50,9 ≈ 305 мкм

г) поле допуска размера определяется исходя из необходимости создать необходимый запас точности 20% (Ta, мкм):

Ta = 1,2∙𝜔 = 1,2∙305 ≈ 366 мкм

д) по таблице ГОСТ 8.051 – 81 выбирается допуск так, чтобы было выполнено условие запаса точности

Для выбранного номинального размера определяется квалитет (по ГОСТ 8.051 – 81): IT 13. Окончательно выбранное значение допуска: Та = 460 мкм

2. Оценка погрешности способа измерений

Нормативное значение погрешности измерения принимается по таблице ГОСТ 8.051 – 81: Δизм = ± 100 мкм. Диапазон погрешностей составляет: Т_ИЗМ = 200 мкм.

Для расчета погрешности способа измерений определяется стандартное отклонение ошибки измерения (Sси, мкм):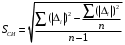



Для расчета можно использовать вспомогательную таблицу 1.2

Таблица 1.2

Параметр	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21	22	23	24	25	∑
|Δ |, мкм	50	10	0	30	70	40	50	140	130	60	40	10	10	10	10	20	10	20	40	10	10	10	30	30	20	860
Δ2 , мкм	2500	100	0	900	4900	1600	2500	19600	16900	3600	1600	100	100	100	100	400	100	400	1600	100	100	100	900	900	400	59600

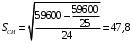За погрешность способа измерений принимается величина поля рассеяния погрешностей измерения, принятое по нормальному закону распределения (𝜔 СИ, мкм): 𝜔_СИ = 6∙S = 6∙47,8 ≈ 287 мкм

Способ измерения считается применимым, если выполняется условие:

𝜔_СИ ≤Т_ИЗМ

Условие не выполняется
3. Проверка гипотезы и случайности и непреднамеренности отбора деталей выборки

Для проверки гипотезу составляется и заполняется исходная таблица

№	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21	22	23	24	25
Размер детали, измеренный микрометром a* мм	60,05	60,04	60,05	60,02	60,07	60,14	60,10	60,01	60,08	60,11	60,06	60,04	60,06	60,04	60,06	60,07	60,04	60,08	60,06	60,04	60,06	60,14	60,12	60,07	60,07
Ранжированный ряд	60,01	60,02	60,04	60,04	60,04	60,04	60,04	60,05	60,05	60,06	60,06	60,06	60,06	60,06	60,07	60,07	60,07	60,07	60,08	60,08	60,1	60,11	60,12	60,14	60,14
Стилизованный ряд	-	-	-	-	+	+	+	-	+	+	0	-	0	-	0	+	-	+	0	-	0	+	+	+	+

Определим медиану ранжированного ряда, полученного микрометром ( , мм)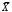

= 60,06

Подсчитывается число серий γ и определяется протяженность самой длинной серии τ: γ = 10; τ = 4.

Составляются и оцениваются неравенства: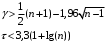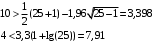





Вывод

О применимости метода измерений: т.к. условие 𝜔_СИ ≤Т_ИЗМ не выполняется, то метод измерения штангенциркулем не применим.

О случайности выборки: т.к. неравенства для γ и τ выполняются , то гипотеза о случайности и непреднамеренности отбора подтверждается.